[python/백준/DP] 2225: 합분해

문제

풀이

case 1) k = 1 경우의 수

n = 1 (1)                                                      => 1개 
n = 2 (2)                                                      => 1개 
n = 3 (3)                                                      => 1개 

case 2) k = 2

n = 1 (0,1) (1,0)                                              => 2개 
n = 2 (0,2) (2,0) (1,1)                                        => 3개  
n = 3 (0,3) (3,0) (1,2) (2,1)                                  => 4개

case 3) k = 3

n = 1   (0,0,1) (0,1,0) (1,0,0)                                 => 3개  

n = 2    (0,0,2) (0,2,0) (2,0,0), (1,1,0) (1,0,1), (0,1,1)      => 6개  

n = 3   (0,0,3) (0,3,0), (3,0,0), (1,1,1), (1,2,0),
        (1,0,2), (0,1,2), (2,1,0), (2,0,1), (0,2,1)             => 10개 

n = 4   (0,0,4), (0,4,0), (4,0,0), (1,1,2), (1,2,1), 
        (2,1,1), (0,1,3), (1,0,3), (1,3,0), (0,3,1), 
        (3,0,1), (3,1,0), (2,2,0), (0,2,2), (2,0,2)            => 15개 

case 4) k = 4

    n = 1 				                                       => 4개 

    n = 2 			                                           => 10개 
        (0,0,0,2) -> 4!/3! -> 4개 
        (0,0,1,1) -> 4!/2!2! -> 6개 

    n = 3                                                      => 20개 
        (0,0,0,3) -> 4!/3! -> 4개
        (0,1,1,1) -> 4!/3! -> 4개
        (0,0,1,2) -> 4!/2! -> 12개

위 내용을 테이블 형태로 표현해보면 다음과 같다.

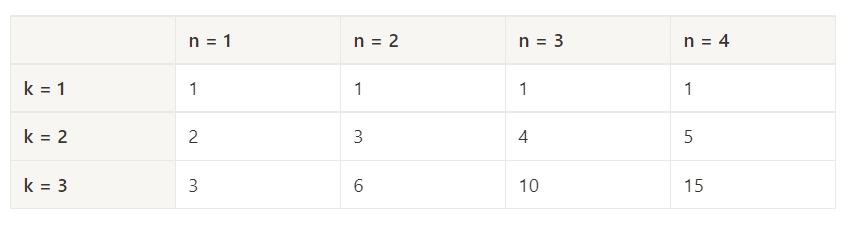
n = 1일 때, 항상 경우의 수는 k이다.
k = 1일 때, 항상 경우의 수가 1이다.

그리고 k와 n이 2보다 클 경우 dp[k][n] = dp[k-1][n] + dp[k][n-1] 인 것을 확인할 수 있다. (표 참고)

따라서 점화식은
dp[k][n] = dp[k-1][n] + dp[k][n-1] (단, k와 n은 1보다 큰 자연수) 이다.

코드

n, k = map(int, input().split())

dp = [[0]*201 for i in range(201)]

# k = 1, n =1 초기화 
for i in range(201):
    dp[i][1] = i
    dp[1][i] = 1

for i in range(2,201):
    for j in range(2,201):
        dp[i][j] = dp[i-1][j]+dp[i][j-1]

print(dp[k][n]%1000000000)