Shannon's information theory

• Shannon의 Entorpy 정의로 해당 정보를 이진수로 인코딩하여 신뢰성 있게 전송하기 위해 필요한 최소 채널 용량을 결정할 수 있음
  • 하나의 심볼 정보량은 bits 단위로 측정됨
• 인코딩하려는 binary 코드 및 소스들을 최소한의 데이터량으로 정보를 전달하는데에 entopy가 사용됨
  • 정보와 데이터 량은 다름
    • 데이터는 많아도 정보는 적을 수 있음
• 랜덤 변수 확률 분포와 그것에 대한 정보량의 관계

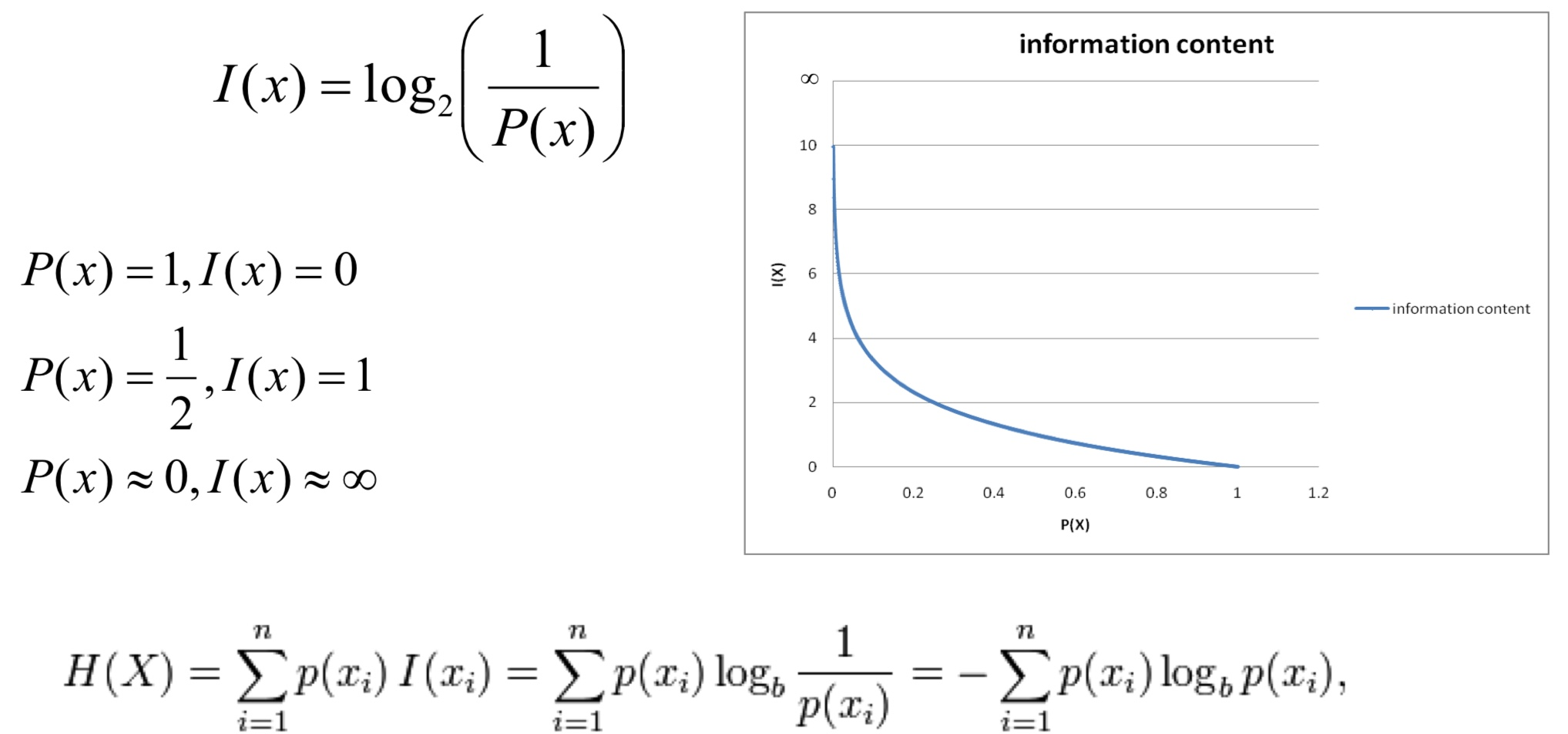
• P(x) = 1, I(x) = 0
  • 특정 정보가 항상 발생한다면 정보가 없는 것이다
• P(x) = 1/2, I(x) = 1
  • 특정 정보가 발생할 확률이 1/2라면 정보를 표현하는데 1bit가 사용된다
• P(x) = 0, I(x) = ∞
  • 특정 정보가 발생하지 않는다면 정보량은 무한하다

Entorypy

• 정보량을 수학적으로 측정하려는 척도
• 예측이 어려운 정보일수록, Entorpy가 높음
  • 동전을 던질 때, 앞/뒤 확률이 50%인 경우(불확실성이 높음)는 엔트로피가 큼
  • 반면, 항상 앞 면만 나오는 동전(불확실성이 없음)은 Entorpy가 0임

Variable length coding(VLC)

• Entropy의 개념을 쉽게 구현한 대표적인 방법으로, 데이터의 발생 빈도에 따라 심볼에 할당되는 비트 길이를 가변적으로 조절하는 방법
  • 각 코드 길이는 음의 로그 값에 비례
    • I(x) = -log_2(P(x))
  • 자주 발생하는 심볼 -> 짧은 코드 할당
  • 드물게 발생하는 심볼 -> 긴 코드 할당
• 입력 심볼을 대응하는 가변 길이의 Prefix Code로 대체함으로써 데이터 압축
• 이렇게 하면 전체 데이터를 표현하는 데 필요한 비트 수가 줄어들어 압축 효율이 높아짐
• 대표적으로 Huffman Coding과 Arithmetic Coding(산술 코딩)이 있음

VLC의 한계

• 이론상 심볼의 발생 확률이 높을수록 해당 심볼을 표현하는 데 필요한 비트 수가 감소해야 함
  • 예 : 발생 확률 𝑃(𝑥)=0.8인 심볼 𝑥는 𝐼(𝑥)=−log⁡_2(0.8)≈0.32 비트로 표현 가능
• 하지만, VLC는 아무리 발생할 확률이 높다고 할지라도 최소 1 Bit를 사용
• 비트의 오류만 발생해도 그 이후의 모든 심볼 해석이 영향을 받을 수 있다

Arithmetic Coding(산술 코딩)

• Huffman coding의 한계를 극복해서 Shannon의 이론에 근접
• 여러 심볼(블록)을 한 번에 처리하여 압축하는 방식
  • 단일 심볼 단위로 코딩할 경우, 심볼별로 확률에 따라 구간을 좁혀야 함
    • 메시지 길이가 길어지면 반복 계산이 늘어나 효율이 떨어질 수 있음
• 산술 코딩은 특정 구간에서 시작하며, 각 심볼의 확률을 이용해 구간을 점점 좁혀나감
• 압축을 달성하기 위해, 발생 확률이 높은 심볼은 발생 확률이 낮은 심볼보다 구간을 덜 좁힘
  • 그 결과, 발생 확률이 높은 심볼은 출력에 더 적은 비트를 기여하게 됨

Binary Arithmetic Coding

• Symbol의 랜덤 변수들이 0 아니면 1
  • 만약 Binary가 아닌 값들이라면?
    • Binary로 만든 후 수행
• 각 이진 심볼에 대해 확률 모델을 사용하여 심볼의 확률을 추정
  • 심볼의 확률 분포에 따라 구간을 조정하여 데이터를 부호화 함
  • 압축 과정은 [0,1) 구간에서 시작
  • 각 심볼의 확률을 기준으로 구간을 나누고, 메세지를 표현하는 구간을 점진적으로 좁혀 나감
  • 확률과 구간 크기 관계
    • 발생 확률이 높은 심볼은 더 큰 구간을 차지
    • 발생 확률이 낮은 심볼은 더 작은 구간을 지
    • 결과적으로, 발생 확률이 높은 심볼은 출력에 적은 비트를 필요로 하고, 확률이 더 낮은 심볼은 더 많은 비트를 필요로 함
• 이 확률 추정치를 기반으로, 코더는 심볼을 실수 범위로 표현하고 이를 이용하여 압축된 이진 코드를 생성
• 인코더에서 압축된 이진 코드를 보내면 디코더에서는 이진 코드를 다시 실수로 변환하고, 이 실수를 기반으로 원래 이진 신호를 복원
• 장점
  • 산술 코딩의 효율성을 유지하면서도 복잡성을 줄일 수 있음
    • 각 심볼이 단지 두 개의 가능한 값만을 가지므로, 확률 모델을 관리하고 업데이트하는 것이 더 간단하기 때문

예시

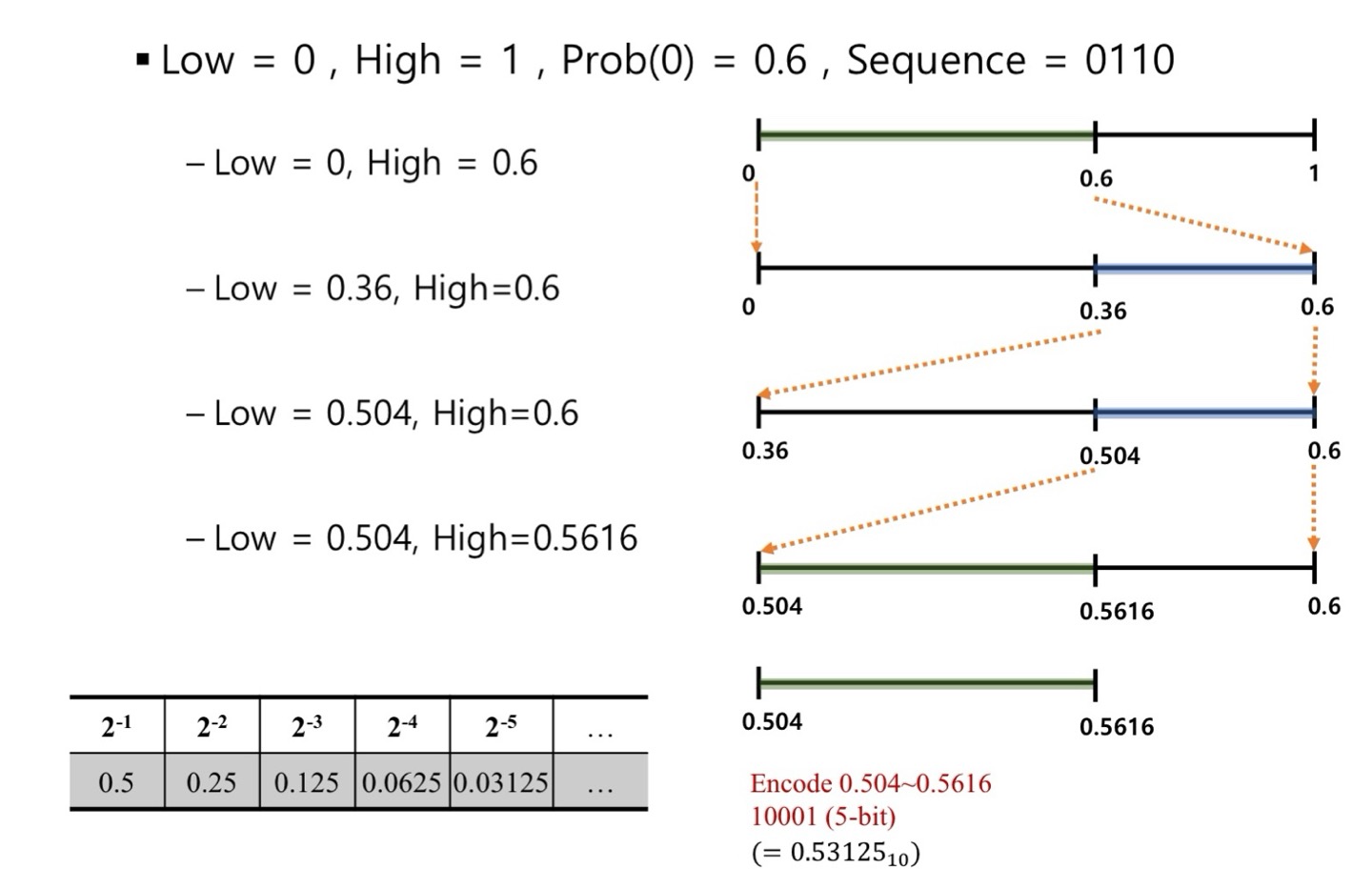
• 조건
  • Low = 0, High = 1 : 구간 0~1
  • Prob(0) = 0.6 : 0일 확률이 0.6
    • 당연히 1일 확률은 0.4
  • Sequence = 0110 : 압축하려는 심볼

인코더

• 0일 확률은 0.6이므로 [0,1] 구간을 6:4로 나눔
  • 0.6이 marker가 됨
  • [0,0.6]과 [0.6,1]을 각각 Range라고 함
• 0을 코딩
  • 0일 확률이 0.6이므로 [0,0.6]의 range를 선정
• [0,0.6] range를 다시 6:4로 나눔
  • 0.36이 marker가 됨
• 1을 코딩
  • 1일 확률이 0.4이므로 [0.36,0.6]의 range를 선정
• [0.36,0.6] range를 다시 6:4로 나눔
  • 0.504가 marker가 됨
• 1을 코딩
  • 1일 확률이 0.4이므로 [0.504,0.6]의 range를 선정
• [0.504,0.6] range를 다시 6:4로 나눔
  • 0.5616이 marker가 됨
• 0을 코딩
  • 0일 확률이 0.6이므로 [0.504,0.5616]의 range를 선정
• [0.504,0.5616] range 중에 가장 적은 비트로 표현되는 수를 선택
  • 예 : 11 (2 bits) (위 그림과는 다른 예시임)
    • 실제는 0.11 -> 10진수로 표현하면 0.525
• 인코더는 0.525를 전송

디코더

• [0,1]의 구간에서 시작했다는 것을 알고 있음
• Prob(0) = 0.6인 것도 알고 있음
• 11을 수신
  • 0.525로 변환
• 0일 확률은 0.6이므로 [0,1] 구간을 6:4로 나눔
  • 0.6이 marker가 됨
• 0.525는 [0,0.6]과 [0.6,1]의 range 중 [0,0.6] range에 있음
  • 0이라는 것을 알 수 있음
• [0,0.6] range를 다시 6:4로 나눔
  • 0.36이 marker가 됨
• 0.525는 [0,0.36]과 [0.36,0.6]의 range 중 [0.36,0.6] range에 있음
  • 1이라는 것을 알 수 있음
• [0.36,0.6] range를 다시 6:4로 나눔
  • 0.504가 marker가 됨
• 0.525는 [0.36,0.504]과 [0.504,0.6]의 range 중 [0.504,0.6] range에 있음
  • 1이라는 것을 알 수 있음
• [0.504,0.6] range를 다시 6:4로 나눔
  • 0.5616이 marker가 됨
• 0.525는 [0.504,0.5616]과 [0.5616,0.6]의 range 중 [0.504,0.5616] range에 있음
  • 0이라는 것을 알 수 있음
• 최종적으로 0110으로 복호화하게 됨

궁금했던 점

• 디코더에서 언제까지 복호하는 지는 어떻게 알지?
  • 심볼 개수 기반
    • 인코더에서 전체 심볼 개수를 전송
    • 디코더에서 해당 심볼 개수만큼 복호하게 되면 종료
  • 종료 심볼 기반
    • 종료 심볼인 EOM(End-of-Message)을 추가 전송
    • 디코더가 EOM을 만나면 종료
• 그냥 4 bits를 보내면 4 bits가 전송되고, Arithmetic Coding을 진행하면 2 bits로 압축되기는 하지만 확률도 전송해야 되고, 종료 조건도 전송해야 되는데 이러면 손해아닌가?
  • Binary Arithmetic Coding은 한 슬라이스를 압축해서 보냄
  • 4 bits 보다 훨씬 긴 심볼을 한 번에 압축하여 전송
    • 길이가 길수록 효율이 좋아짐

Adaptive Binary Arithmetic Coding

• Syntax Element의 정확한 확률을 사전에 알 수 없음
  • 데이터가 매우 다양하거나 구조적으로 복잡할 때, 특정 구문 요소의 발생 확률을 미리 알기 어려움
  • 따라서 확률 분포를 고정된 값으로 사용하기 어려움
• 시간이 지남에 따라 구문 요소의 확률이 변할 수도 있음
  • 데이터 스트림이 진행됨에 따라 구문 요소의 발생 패턴이 바뀔 수 있음
  • 예를 들어, 초기에는 특정 요소가 자주 발생했지만 시간이 지나면서 다른 요소가 더 자주 나타날 수 있음
• 구문 요소의 확률은 인코딩(Encoding)과 디코딩(Decoding) 중에 업데이트 됨
  • 이는 발생하는 심볼에 따라 동적으로 변화하는 데이터에 대해 더 효과적으로 코딩할 수 있게 해줌
• 데이터의 통계적 특성이 시간에 따라 변할 때도 높은 압축률을 유지할 수 있다는 것이 장점
• Initial probability(초기 확률)를 잘 못 설정하면 압축 효율이 떨어질 수도 있다
• 0과 1의 개수가 같으면, 압축하지 않고 전송하는 것과 같은 비트 수를 전송
  • 손해가 없음
• 같은 숫자가 반복될수록 압축 효율이 좋아진다는 특징이 있음

예시 1

• 압축이 성공적으로 되지 못한 경우

• 조건

  • Binary Sequence : 01111
  • Counter variables : C(0), C(1)
  • P(0) = C(0) / {C(0) + C(1)}, P(1) = C(1) / {C(0) + C(1)}

  

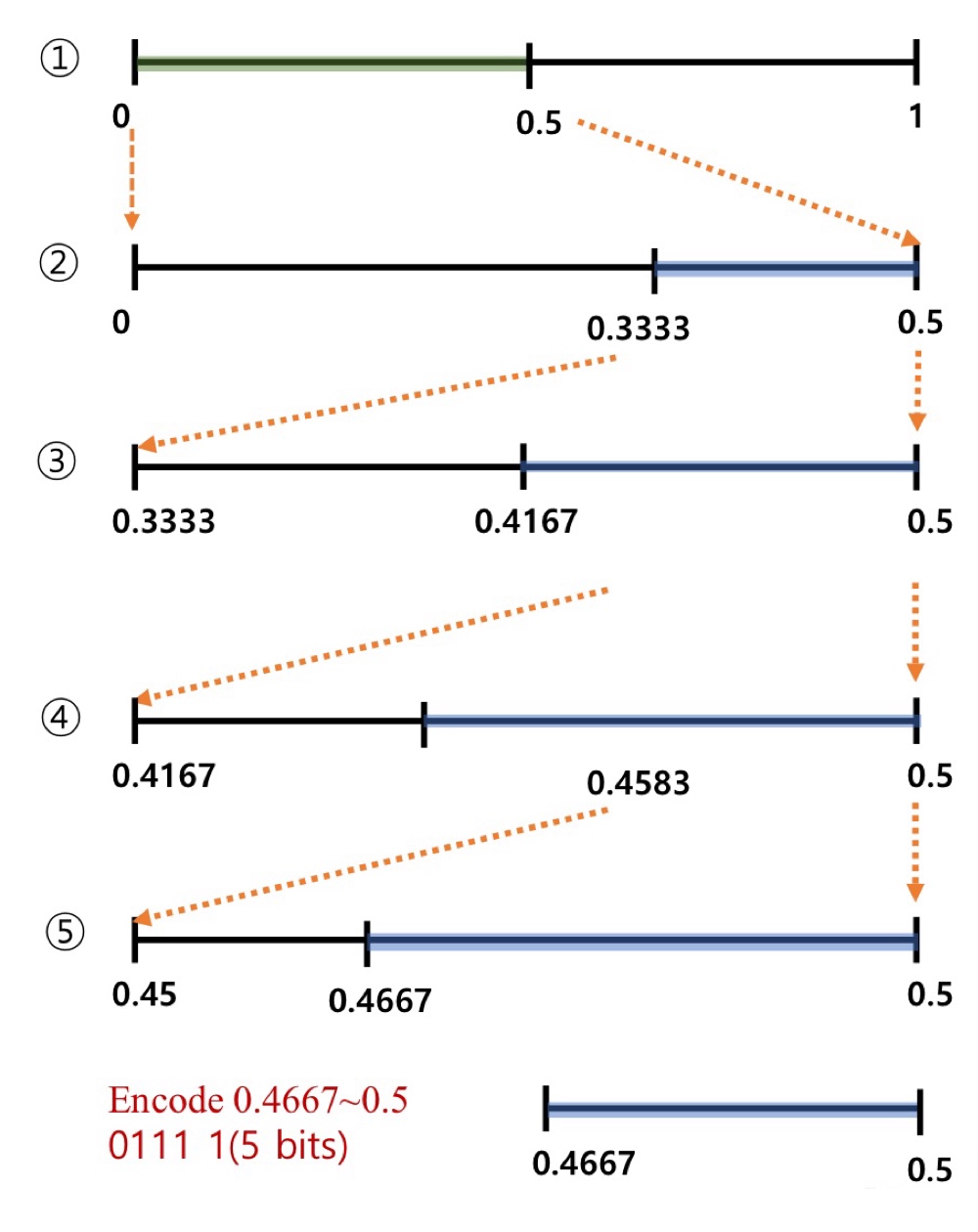
1. 초기값

• C(0) = C(1) = 1
  • P(0) = P(0) = 1/2
• 0일 확률은 1/2 이므로 [0,1] 구간을 1:1로 나눔
  • 0.5가 marker가 됨

2. Encoding 0

• 1/2 확률로 0이 발생
• range는 [0, 0.5]로 선정됨
• 0이 선택되어 C(0) = 2, C(1) = 1
  • P(0) = 2/3, P(0) = 1/3
• [0,0.5] 구간을 2:1로 나눔
  • 0.3333이 marker가 됨

3. Encoding 1

• 1/3 확률로 1이 발생
• range는 [0.3333, 0.5]로 선정됨
• 1이 선택되어 C(0) = 2, C(1) = 2
  • P(0) = 2/4, P(0) = 2/4
• [0.3333,0.5] 구간을 1:1로 나눔
  • 0.4167이 marker가 됨

4. Encoding 1

• 1/2 확률로 1이 발생
• range는 [0.4167, 0.5]로 선정됨
• 1이 선택되어 C(0) = 2, C(1) = 3
  • P(0) = 2/5, P(0) = 3/5
• [0.4167,0.5] 구간을 2:3로 나눔
  • 0.4583이 marker가 됨

5. Encoding 1

• 3/5 확률로 1이 발생
• range는 [0.4583, 0.5]로 선정됨
• 1이 선택되어 C(0) = 2, C(1) = 4
  • P(0) = 2/6, P(0) = 4/6
• [0.4583,0.5] 구간을 1:2로 나눔
  • 0.4667이 marker가 됨

6. Encoding 1

• 4/6 확률로 1이 발생
• range는 [0.4667, 0.5]로 선정됨

7. [0.4667, 0.5] range 중 가장 적은 비트로 표현이 되는 수를 선택

• 0.01111이 선택됨 (5 bits)
• 압축 되지는 않음

예시 2

• 초기값 설정으로 압축이 성공적으로 된 경우
• 조건
  • Binary Sequence : 01111
  • Counter variables : C(0), C(1)
  • P(0) = C(0) / {C(0) + C(1)}, P(1) = C(1) / {C(0) + C(1)}

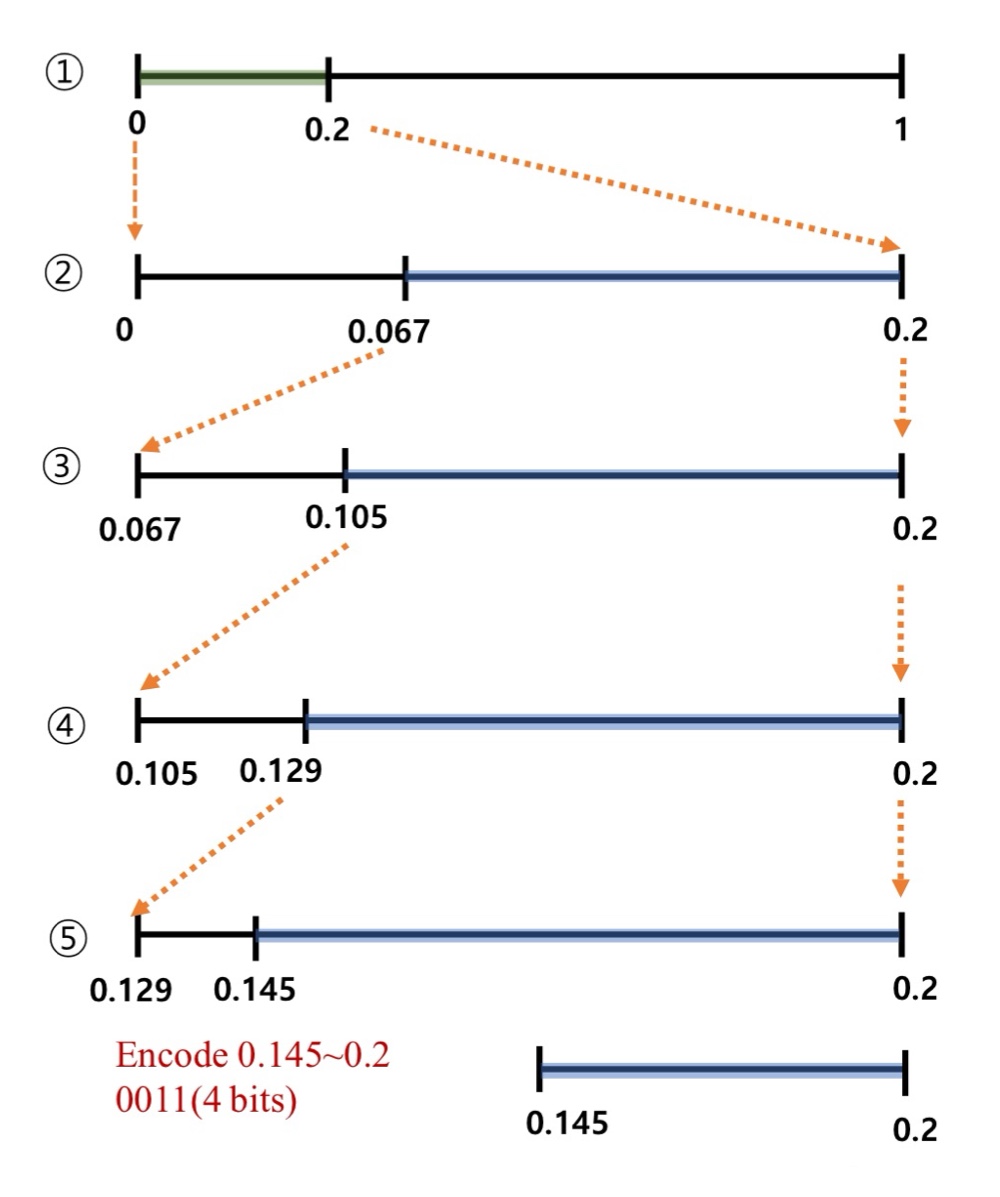
1. 초기값

• C(0) = 1, C(1) = 4
  • P(0) = 1/5, P(0) = 4/5
• 0일 확률은 1/5이므로 [0,1] 구간을 1:4로 나눔
  • 0.2가 marker가 됨

2. Encoding 0

• 1/5 확률로 0이 발생
• range는 [0, 0.2]로 선정됨
• 0이 선택되어 C(0) = 2, C(1) = 4
  • P(0) = 2/6, P(0) = 4/6
• [0,0.2] 구간을 1:2로 나눔
  • 0.067 marker가 됨

3. Encoding 1

• 4/6 확률로 1이 발생
• range는 [0.067, 0.2]로 선정됨
• 1이 선택되어 C(0) = 2, C(1) = 5
  • P(0) = 2/7, P(0) = 5/7
• [0.067,0.2] 구간을 2:5로 나눔
  • 0.105 marker가 됨

4. Encoding 1

• 5/7 확률로 1이 발생
• range는 [0.105, 0.2]로 선정됨
• 1이 선택되어 C(0) = 2, C(1) = 6
  • P(0) = 2/8, P(0) = 6/8
• [0.105,0.2] 구간을 2:3로 나눔
  • 0.129 marker가 됨

5. Encoding 1

• 6/8 확률로 1이 발생
• range는 [0.129, 0.2]로 선정됨
• 1이 선택되어 C(0) = 2, C(1) = 7
  • P(0) = 2/9, P(0) = 7/9
• [0.129,0.2] 구간을 1:2로 나눔
  • 0.145 marker가 됨

6. Encoding 1

• 7/9 확률로 1이 발생
• range는 [0.145, 0.2]로 선정됨

7. [0.145, 0.2] range 중 가장 적은 비트로 표현이 되는 수를 선택

• 0.0011이 선택됨 (4 bits)
• 초기값을 잘 설정하여 압축 효율이 좋아짐

Context

• CABAC의 앞자리 C
• 특정 심볼을 부호화할 때, 그 비트가 나타날 확률에 영향을 미칠 수 있는 주변 정보를 의미
• 다양한 Syntax Element(예: 모드, 잔차, 모션 벡터 등)에 대해 여러 Context를 정의
• 각 Syntax Element는 고유한 Context를 사용하며, 데이터의 특성에 따라 여러 Context 모델을 선택
• Encoder와 Decoder는 동일한 Context 모델을 유지해야 하므로, 부호화 및 복호화 과정에서 Context가 동기화 됨

Entropy Coder

CABAC block diagram

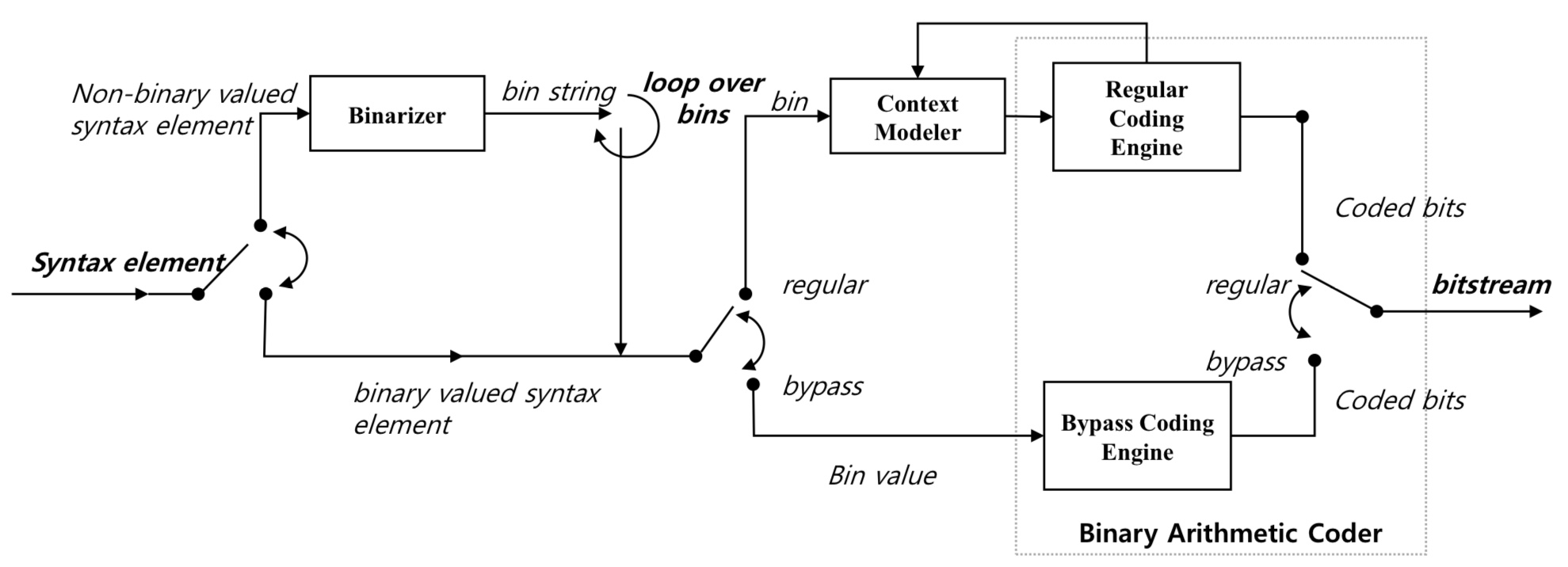
• Syntax Element가 입력으로 들어오면, 먼저 이진화가 필요한지 확인하여 필요한 경우 이진화를 진행
  • 이진화가 필요하지 않은 Syntax Elemnet
    • Flag, MV 등
  • 이진화가 필요한 Sytax Element
    • 블록 분할 모드, 화면간 예측 모드 등
• 이진화까지 진행된 bin string은 1 bit씩 Arithmetic Coding(산술부호화)을 진행
• 입력된 bit가 Bypass 모드인지 Regular 모드인지는 Syntax Element의 유형과 비트의 위치에 따라 결정됨
• Bypass
  • 이름 그대로 그냥 전송하는 것 같지만, 실제로는 Regular 모드와 동일하게 동작함
  • 단지 확률을 1/2로 가정하고, Shift 연산 등만 하여 계산량이 적기 때문에 Bypass라고 불림
  • Context를 사용하지 않는다는 차이점도 있음
    • 계산량이 적어짐
  • 실제로 Regular Coding Engine으로 확률을 1/2로 가정하고 처리하면 동일한 동작을 수행하게 됨
• Regular
  • Context Moduler
    • 각 bin에 대해 Context 기반 확률 모델링을 적용하여 부호화할 확률을 계산
    • 예를 들어, 이전에 부호화된 bin의 값이나 주변 블록의 특징을 기반으로 현재 bin의 확률을 예측
  • Regular Coding Engine
    • Arithmetic Coding 수행
    • 0과 1이 발생할 때마다 확률 업데이트를 진행
• Arithmetic Coding을 수행하면 1bit씩 출력
  

Binarization

• 각 심볼을 이진 문자열(binary string)로 변환하는 과정
  • 이진수가 아닌 경우에만 진행
• 이진화 이후에는 이진 코드에 컨텍스트 모델링과 산술 코딩이 순차적으로 적용됨
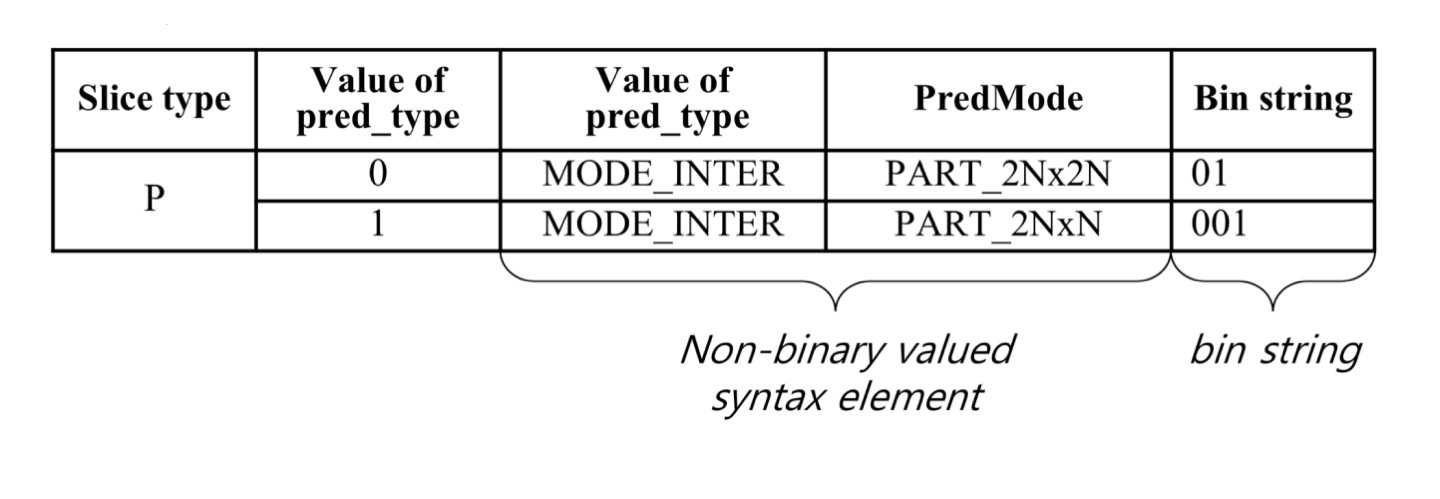
• Syntax Element 마다 어떤 Binarization을 사용할지 정해져 있음
  • 예 : 분할 모드 같은 경우 테이블 방식으로 정해져 있음

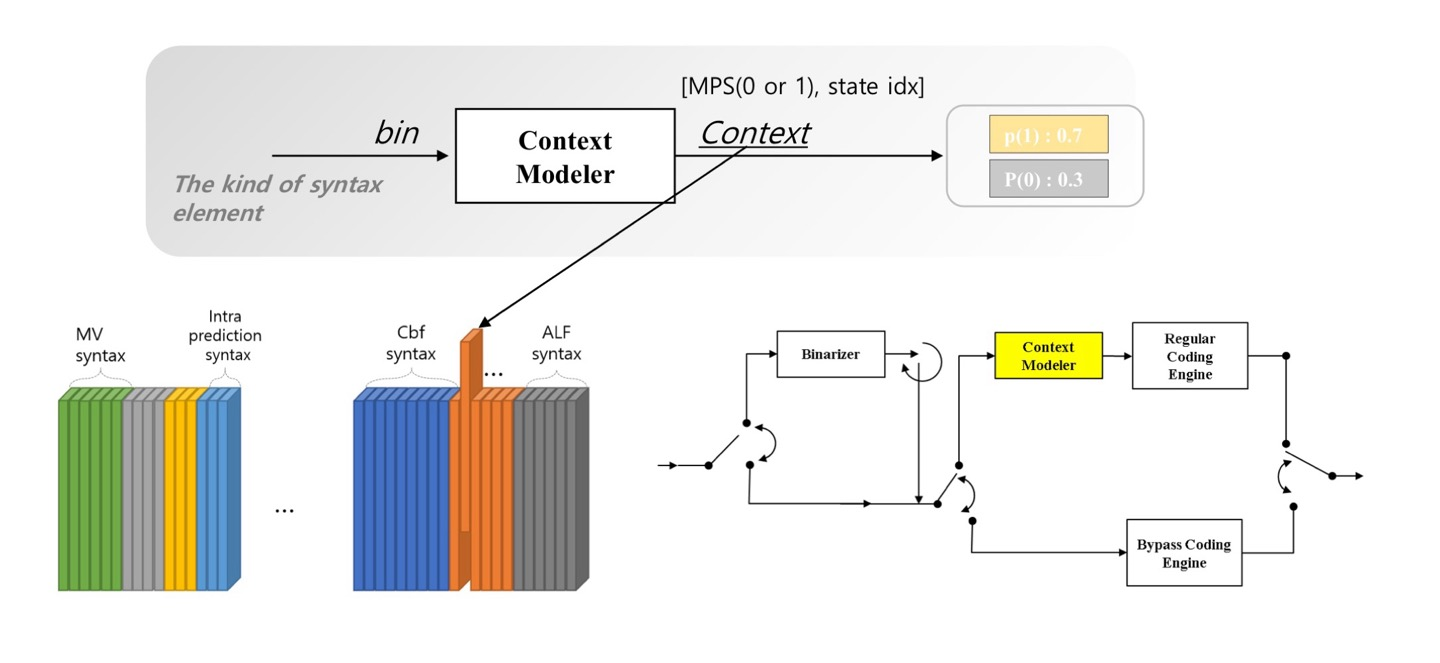
Context modeling

• 메모리 안에 Context들이 저장되어 있음
  • 모든 Syntax Element에 대해 Context들이 저장되어 있음
  • Syntax Element 마다 여러 Context가 저장되어 있음
• 주변 블록이나 이전 bin을 보고 LPS(Less Probable Symbol)와 MPS(Most Probable Symbol)의 확률을 결정
• LPS의 확률과 pState Index를 Regular Coding Engine으로 전달

LPS(Less Probable Symbol)

• 확률이 0.5 보다 적은 심볼을 의미
• 값의 범위 : [0,0.5]
• 즉, 현재 컨텍스트에서 나타날 확률이 더 낮은 심볼

MPS(Most Probable Symbol)

• 확률이 0.5 보다 큰 심볼을 의미
• 값의 범위 : [0.5,1]
• 즉, 현재 컨텍스트에서 나타날 확률이 더 높은 심볼

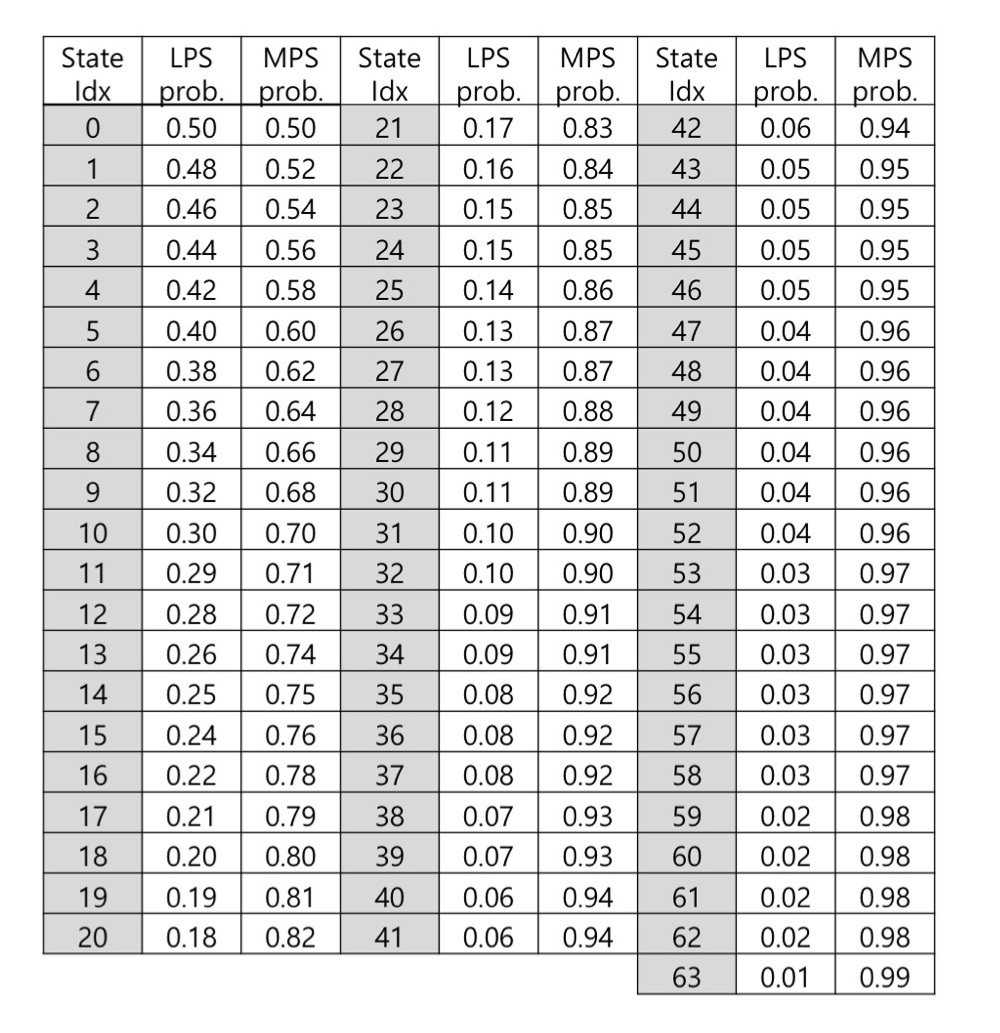
pState Index

• LPS 확률을 인덱스화한 것
  • 양자화를 통해 인덱스로 표현
• LPS와 MPS의 확률을 간접적으로 표현
  • pState Index를 통해 현재 Context에서 LPS가 발생할 확률을 알 수 있음
• 확률 값을 업데이트할 때는 인덱스 값만 변경하면 됨

Initialization process for context variables

• Slice 단위로 Context 초기화 작업을 진행
  • Syntax Element 마다 LPS의 확률과 pState Index를 초기화 진행
• 업데이트 시 pState Index만 변경하여 LPS 확률값 조정

예시 1

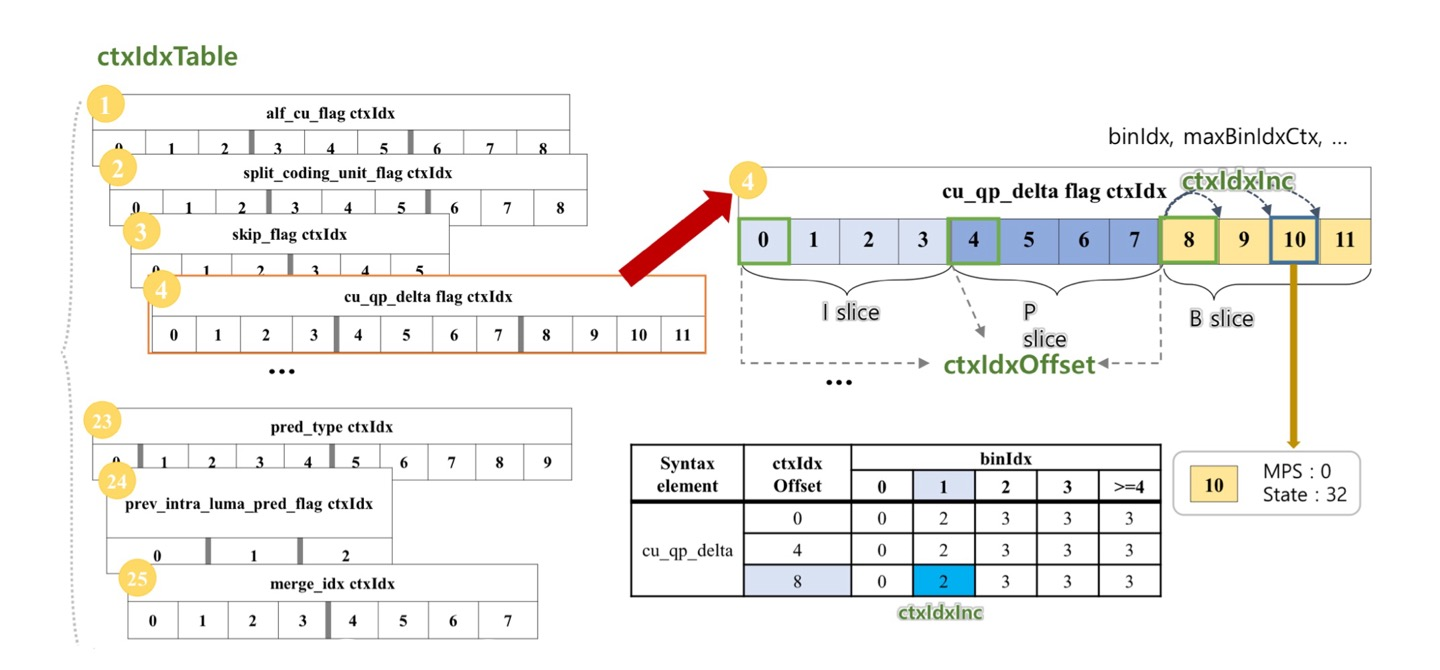
• 조건
  • Syntax Element : cu_qp_delta flag
  • Slice Type : B slice
  • binIdx : 1
• ctxIdxTable에서 cu_qp_delta flag ctxIdx 정보를 가져옴
• B slice 이고, binIdx가 1 이므로 표에 의해 2라는 것을 알 수 있음

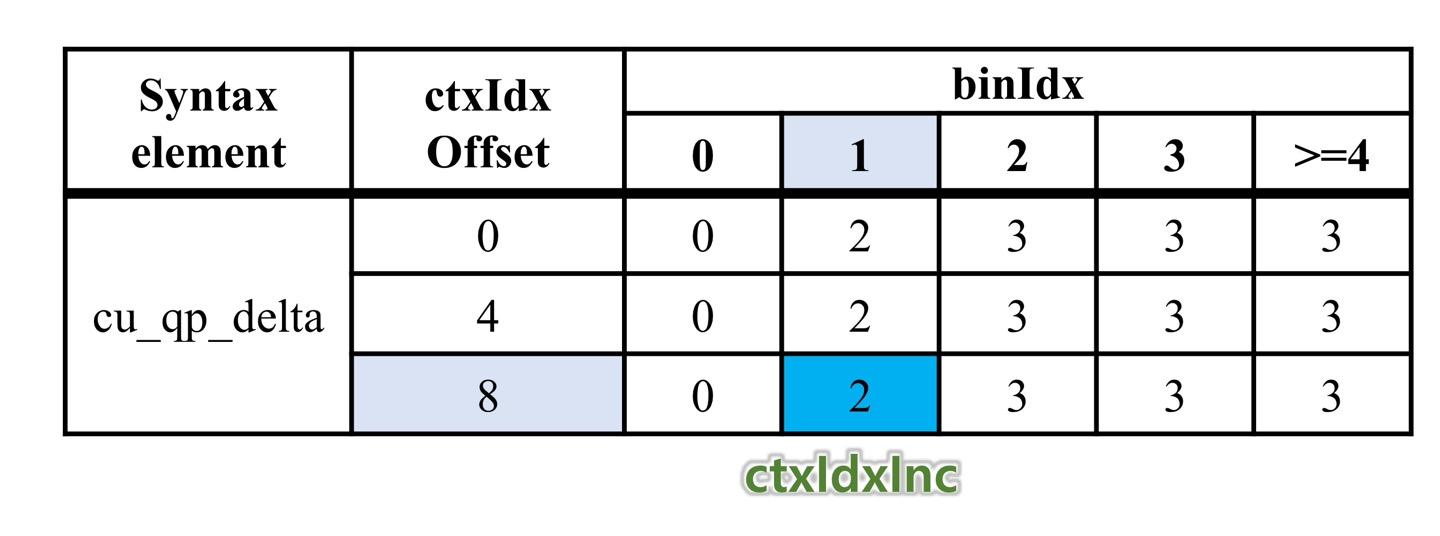
• 8 + 2로, 10번 Context를 가져옴
  • MPS가 0이고, pState Index가 32

예시 2

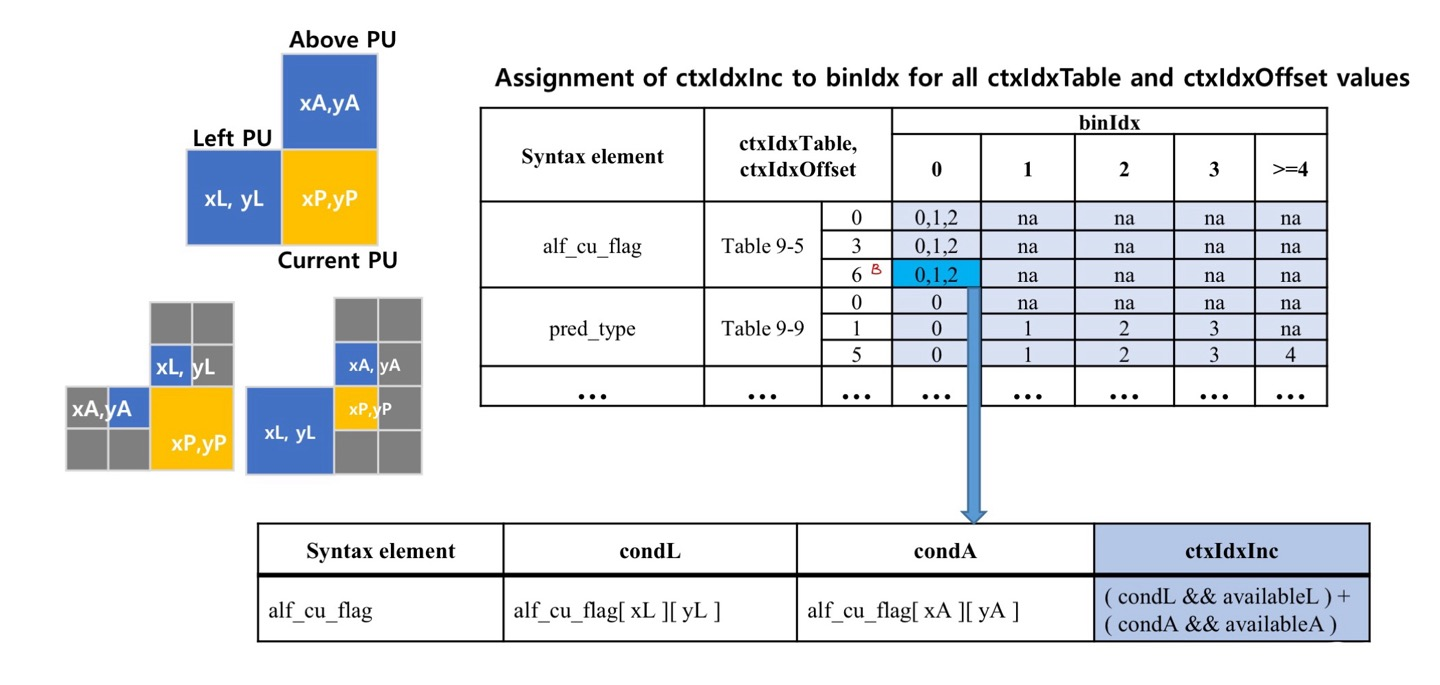
• 조건
  • Syntax Element : alf_cu flag
  • Slice Type : B slice
  • binIdx : 0
• 조건에 의해 Context를 정했는데도 0, 1, 2가 선택됨
• 이 경우에는 추가 조건이 있음
  • 현재 주변 블록들(왼쪽 블록, 위쪽 블록)이 가용 가능한지, 몇 개가 가용 가능한지
  • 0 : 왼쪽 블록, 위쪽 블록 둘 다 가용 불가능한 경우
  • 1 : 왼쪽 블록이나 위쪽 블록 중 하나만 가용 가능한 경우
  • 2 : 왼쪽 블록, 위쪽 블록 둘 다 가용 가능한 경우
• 주변 블록이 둘 다 가용 가능하면, binIdx가 0일 확률이 높고, 하나만 가용 가능하면 1일 확률이 높다는 등의 확률적 특성을 갖기 때문에 각각 다른 Context를 사용

Regular coding engine

• 심볼을 이진화한 후, Context Modeling을 통해 얻은 확률 정보를 사용하여 Arithmetic Coding 진행
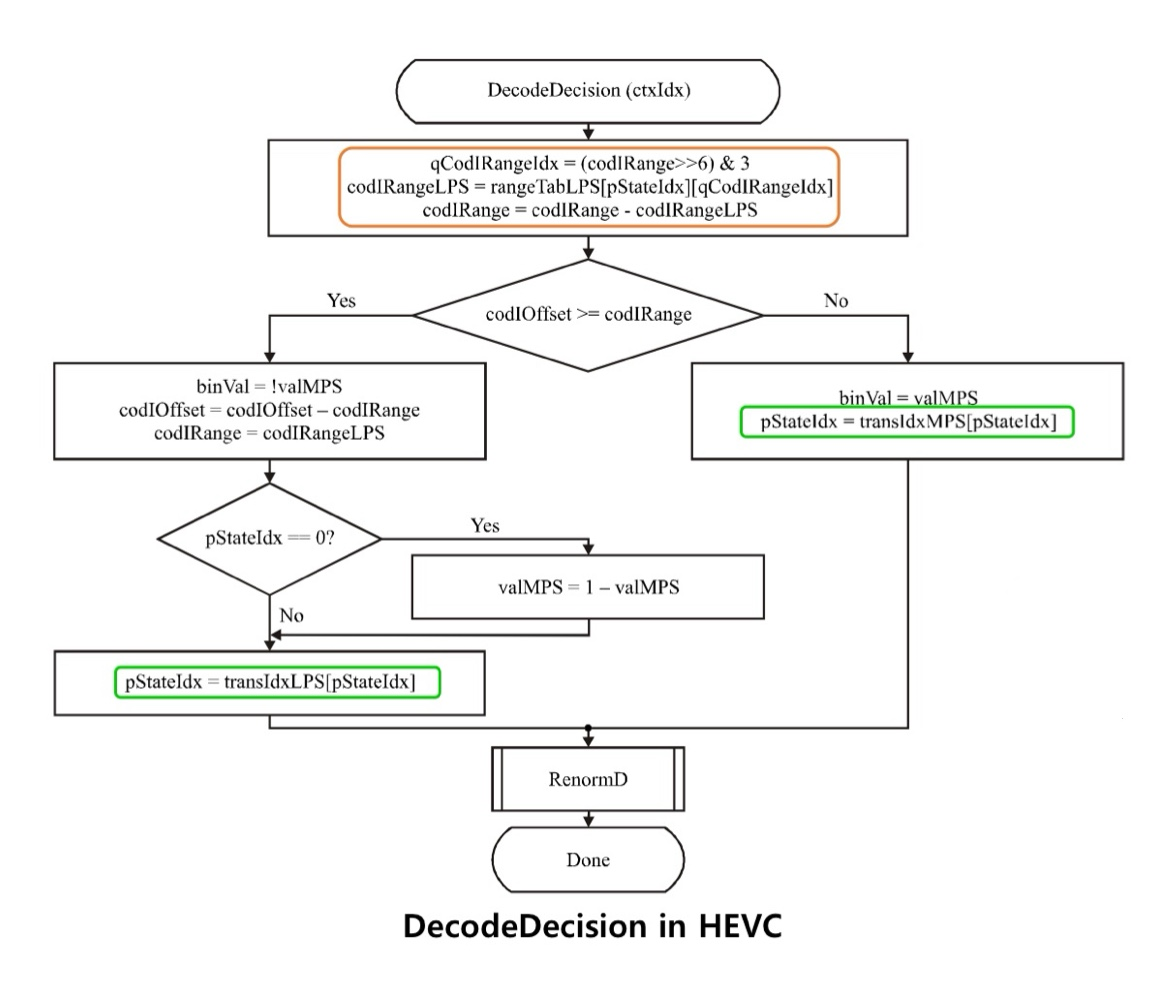
• LPS, pState, binVal(입력된 bin 값)의 값을 바탕으로 MPS range와 LPS range를 결정
• 앞선 BAC(Binary Arithmetic Coding)과 ABAC(Adaptive Binary Arithmetic Coding)의 예시에서는 Range의 범위가 [0,1]이지만, 실제 HEVC에서는 9 bits를 처리하는 방식을 사용하기 때문에 범위가 [0, 510]임
  • 2의 9승은 512로 [0, 511]이지만, 511을 사용할 경우 정확히 반으로 나눠지지 않는 문제점이 있음
  • 확률이 0.5인 경우는 중요하기 때문에 짝수를 만들어 주기 위해 510을 사용
• Range 범위가 256 보다 작아지면 renormalization을 수행
  • Range가 작아지면 에러가 심해질 수 있기 때문
  • 이 때, Range 값의 두 배로 늘림

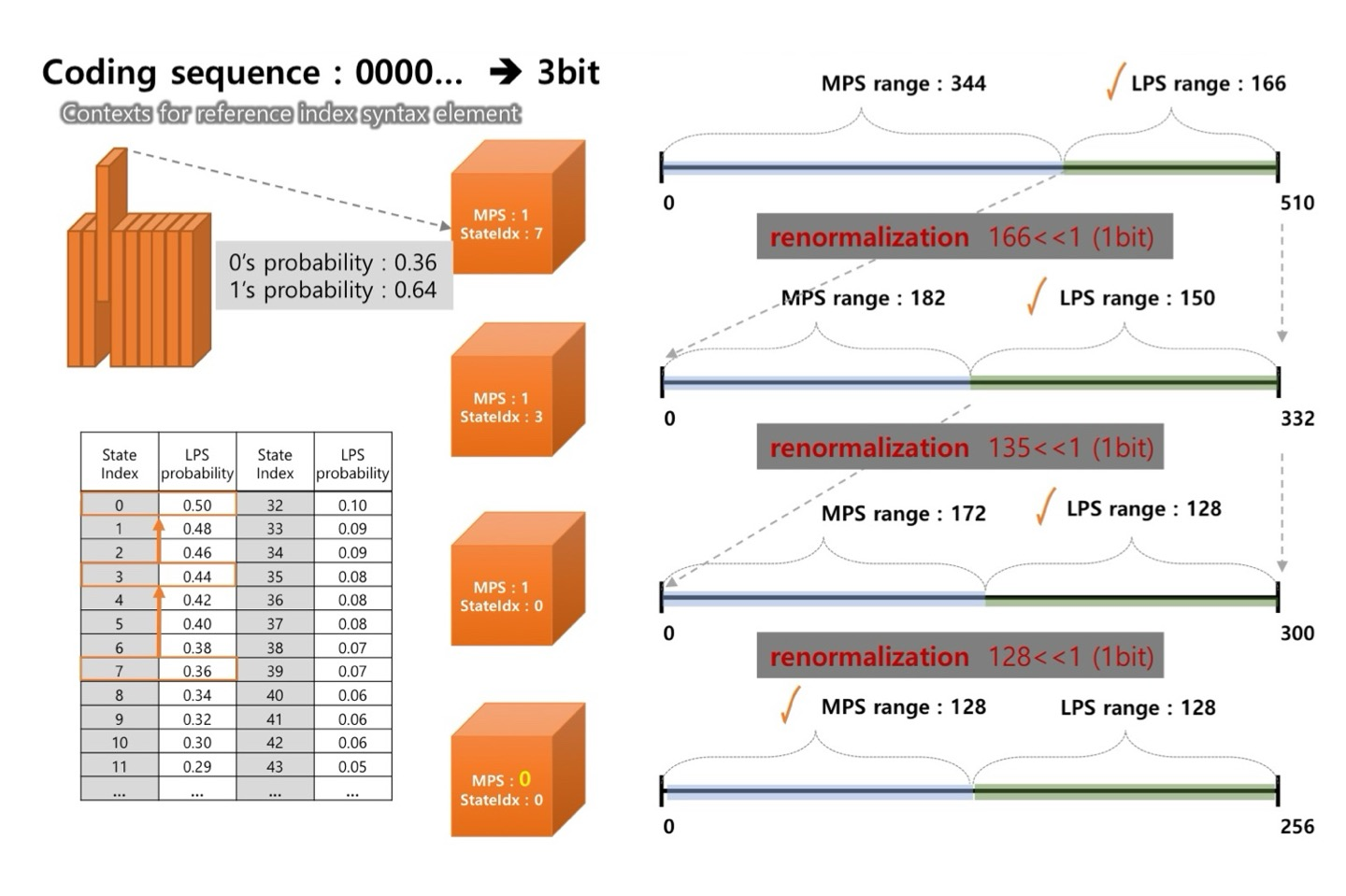
예시

• 입력으로 0 0 0이 들어온 상황

• Context
  • MPS : 0
    • 0이 나올 확률이 높음
  • pState Idx : 22
  • binVAl(입력) : 0
    • 실제 0이 입력됨
• Total Range(510)과 pState Idx를 Regular Coding Engine에 입력을 넣어주면 MPS와 LPS Range를 계산
  • 실제로는 Total Range(510)과 pState Idx를 입력으로 넣어주면 LPS Range를 알려주는 테이블이 있음
  • MPS Range는 Total Range에서 LPS Range를 빼줘서 계산
• 0이 입력 되었으므로 MPS Range가 선택됨

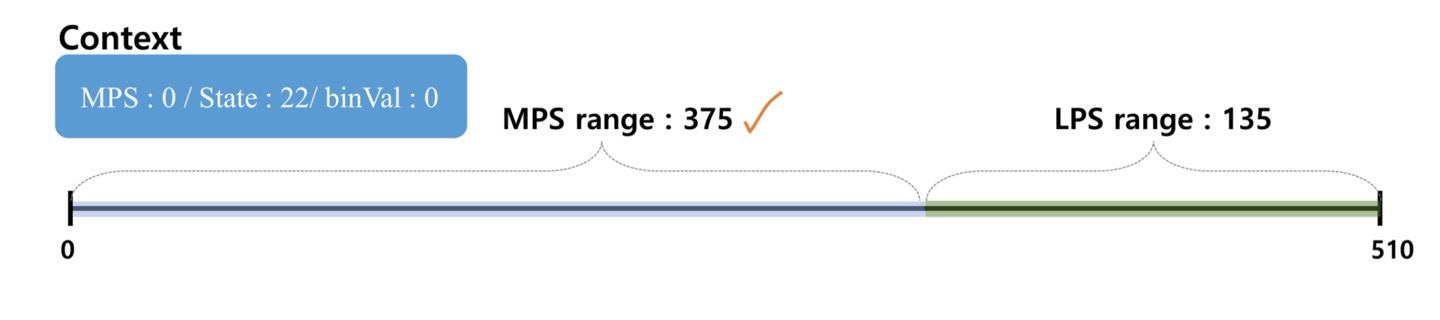
• Context에 의해 Range를 나눠줌
• 또, 0이 입력 되었으므로 MPS Range가 선택됨

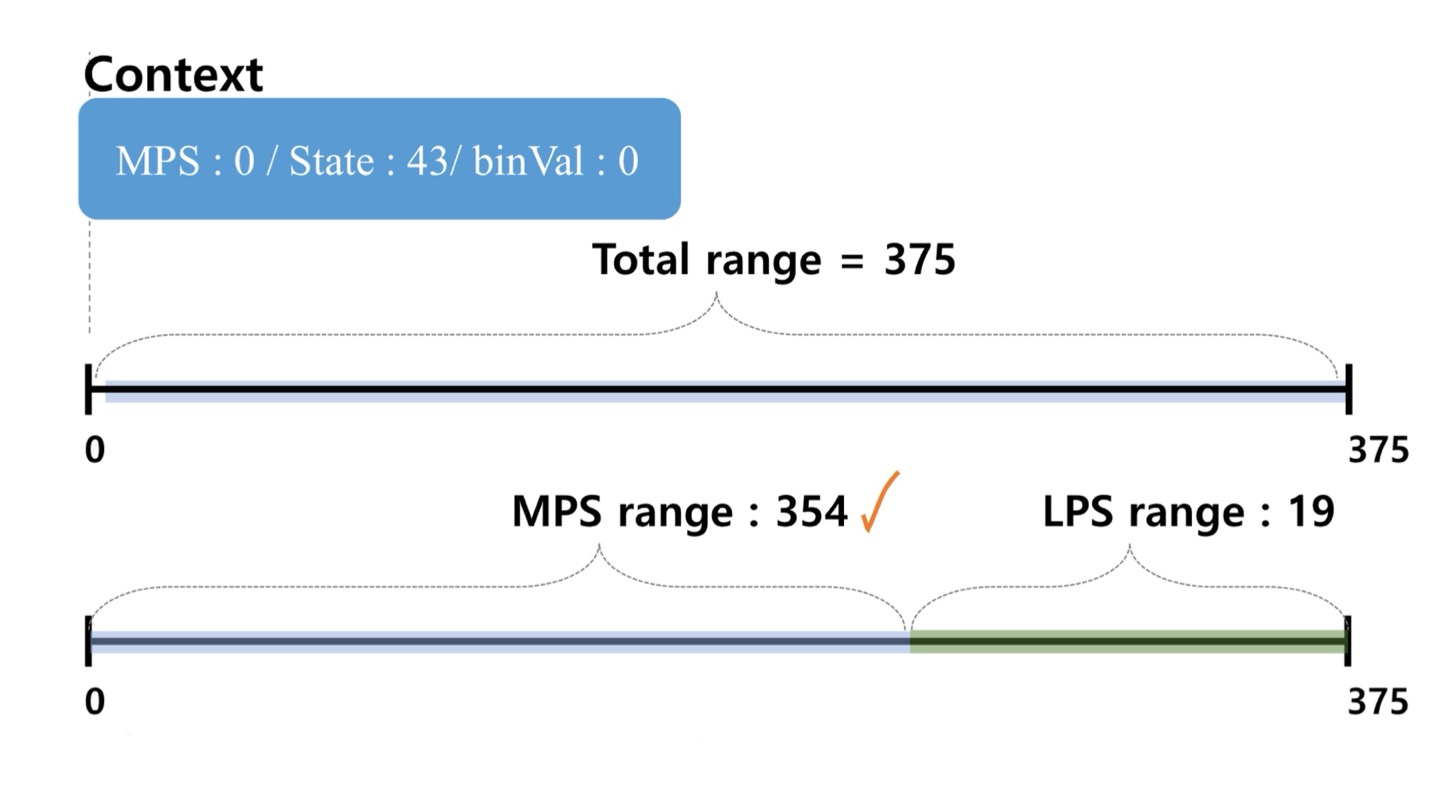
• Context에 의해 Range를 나눠줌
• MPS Range가 256보다 작으므로 renormalization 수행

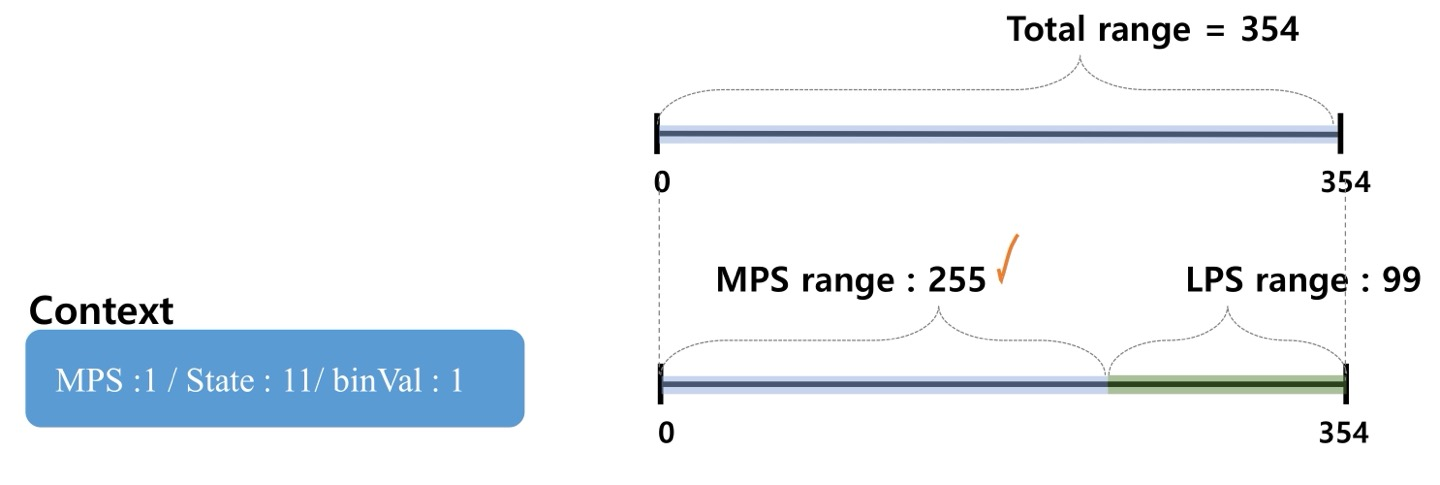
• 255를 2배로 양자화하여 510으로 늘림
  • 이 때, shift 연산으로 2배로 늘림
  • shift 연산으로 인해 1 bit가 추가되는데, 기존 9 bits에서 1 bit가 추가되어 10 bits가 됨
  • HEVC는 9 bits로 정해져 있기 때문에 1 bit를 내보내 출력하게 됨
  • 출력으로 나온 bin을 bit stream으로 사용

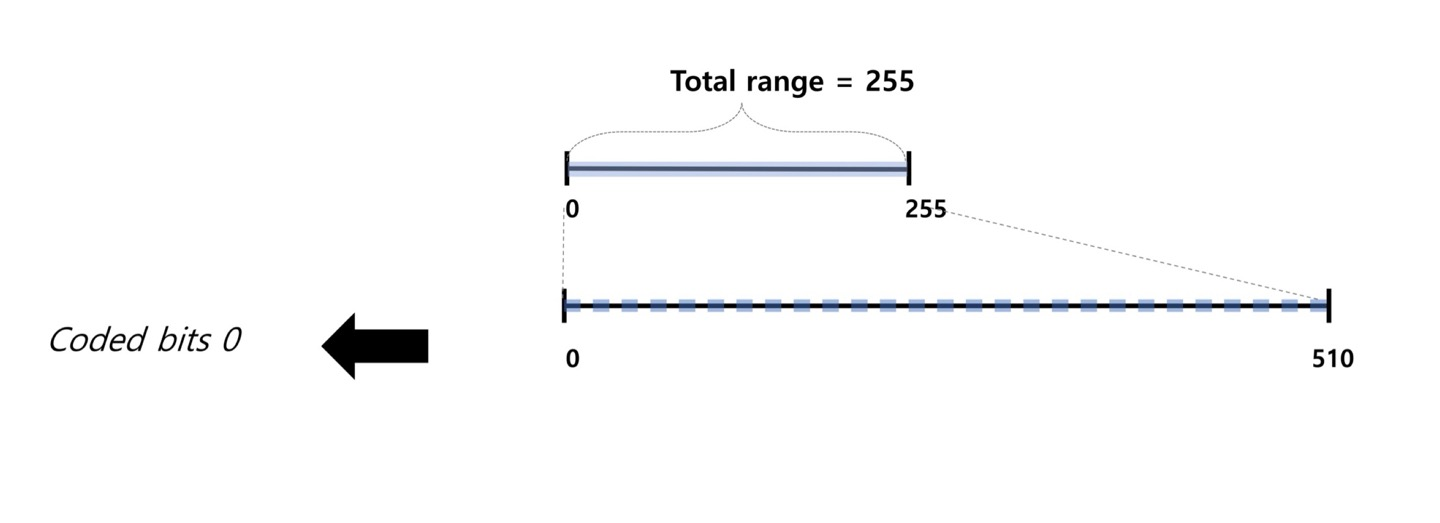
• CABAC은 bin 하나하나 Arithmetic Coding할 때마다 bit stream이 출력되는 것이 아니라 Range가 256보다 작아지게 되면 그 때 bit stream이 출력됨

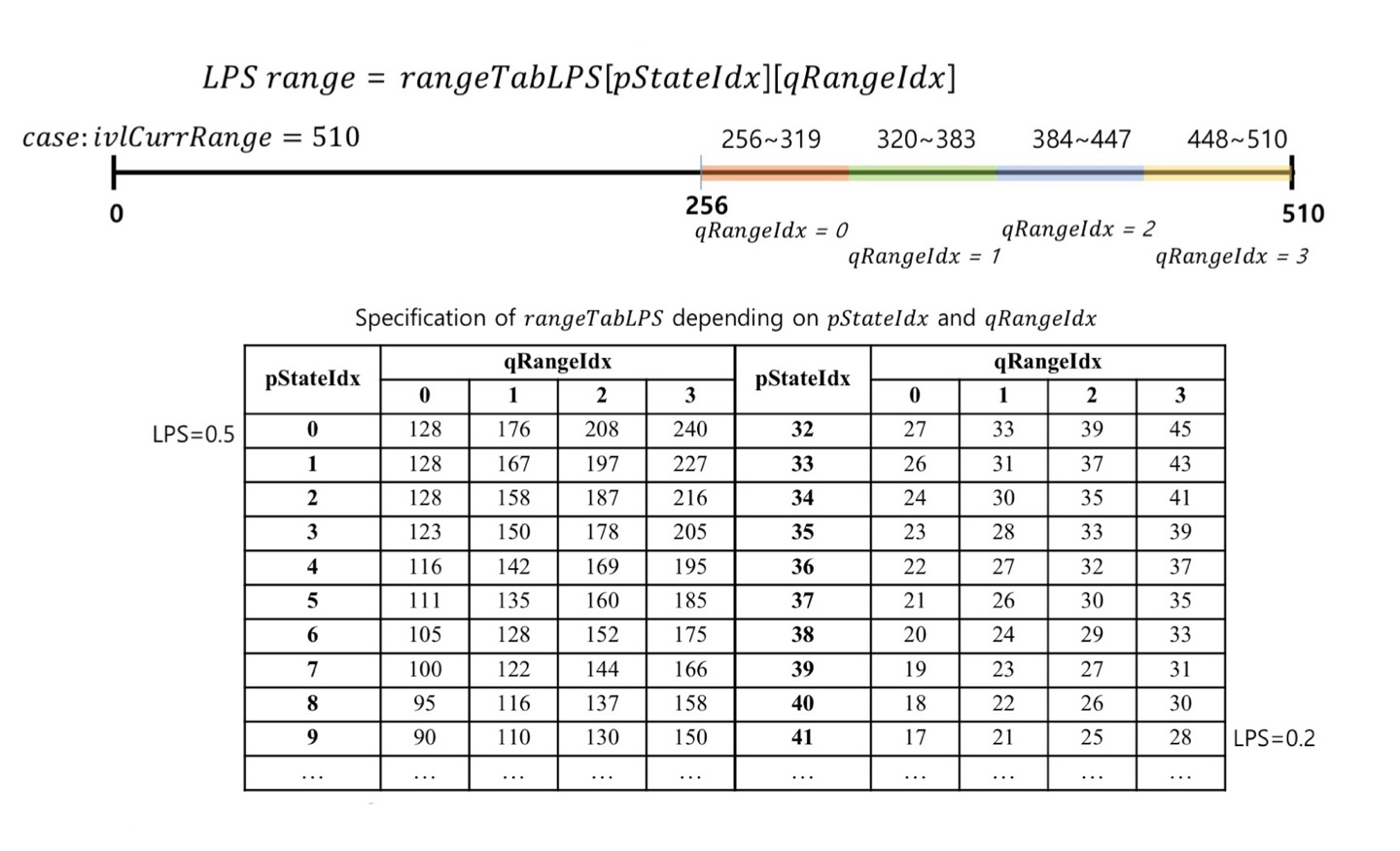
Binary Arithmetic Coding - Table based

• 앞서,Total Range와 pState Idx로 LPS Range를 알려주는 Table이 있다고 언급
• HEVC의 Range는 항상 9 bits로 표현되고, 상위 비트는 항상 1로 시작
  • 의미 없는 정보
• 그 다음 2 bit를 LPS Range를 계산하는데 사용
  • 이 2 bits에 의해 4 가지 경우로 구분하여 LPS Range를 계산 할수 있음

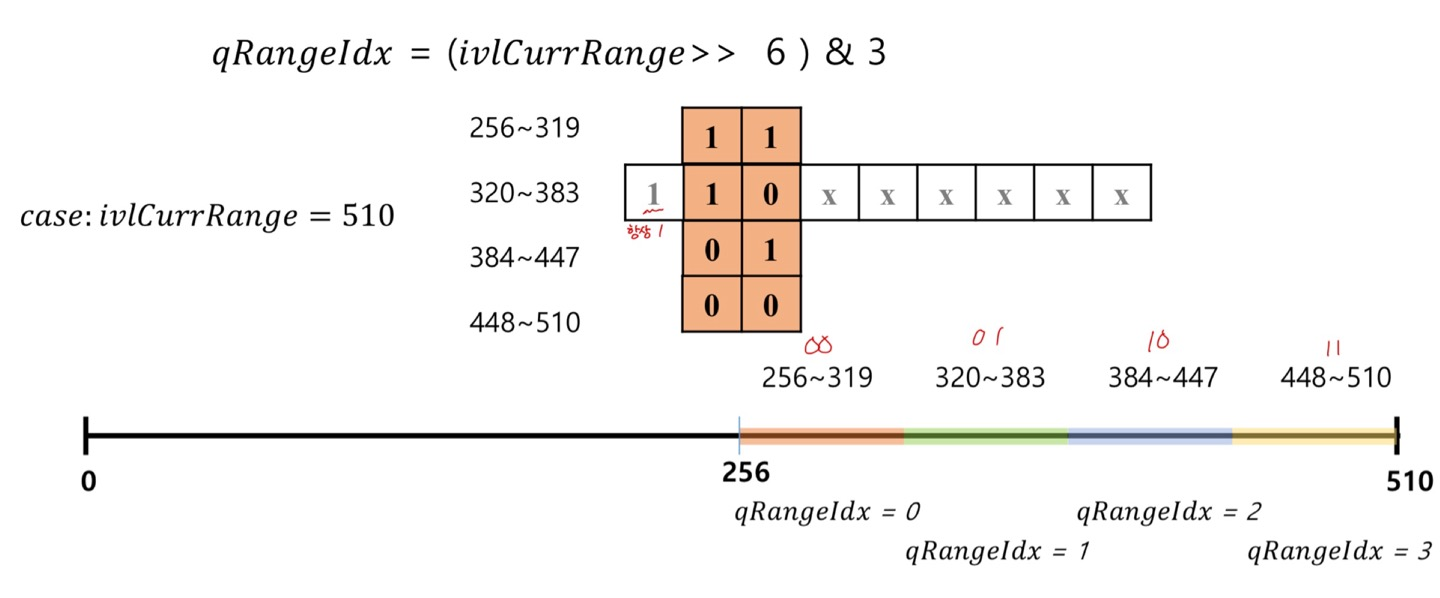
• rangeTabLPS에서 Total Range와 pState Idx를 통해 LPS Range를 알 수 있음

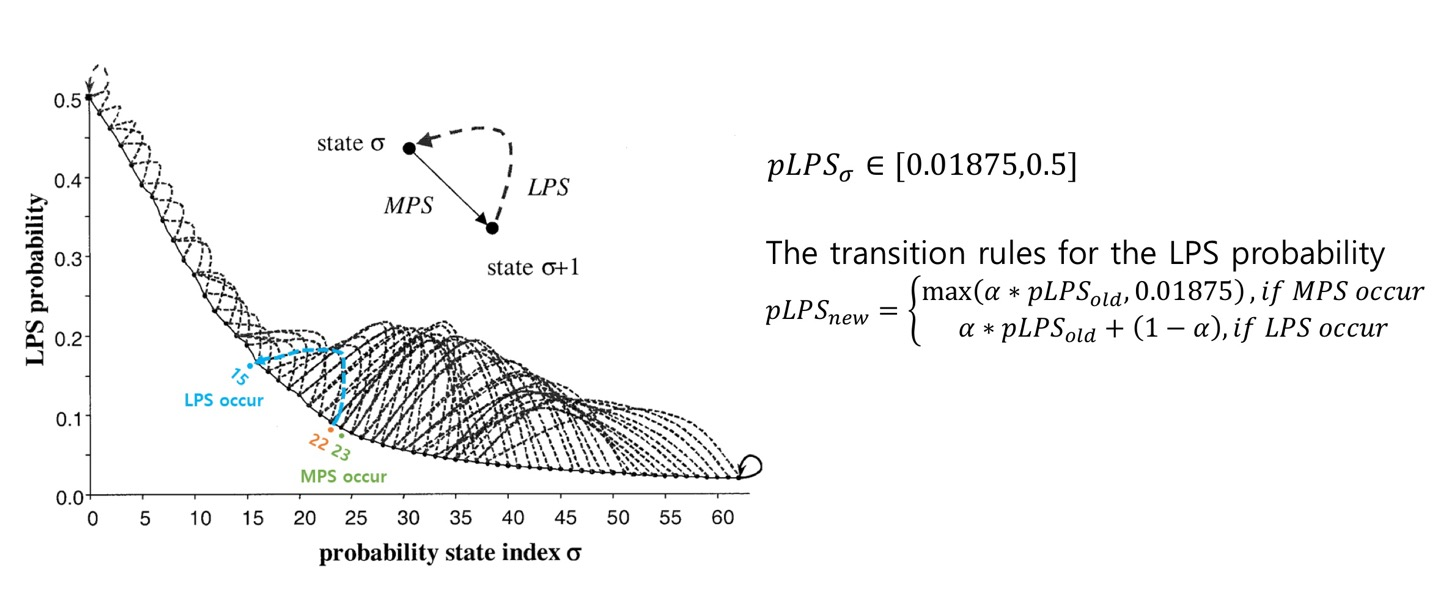
Probability Update

• MPS 또는 LPS가 나타날 때마다 해당 Context의 확률 업데이트
  • 확률을 더 정확하게 예측하기 위해 필요한 과정
• 이렇게 업데이트된 확률은 다음 심볼의 코딩을 위해 사용되며, 이를 통해 데이터 압축의 효율성이 높아지게 됨
• 우연치 않게 LPS가 계속 발생하는 경우 LPS range를 늘려준다
  • 이 때, pState Idx를 감소시킴
    • LPS 확률을 높여줌
    • LPS Range가 늘어나게 됨
• pState Idx가 0인 경우(LPS의 확률이 0.5인 경우)에도 LPS가 발생한다면 MPS와 LPS가 반전됨
  • 예전 MPS는 새로운 LPS가 됨

• 아래 그래프는 업데이트 과정을 도식화한 것

코드

if ( binVal == valMPS )  # MPS가 발생했을 경우
	pStateIdx = transIdxMPS( pStateIdx )  # 아래 table을 보고 pStateIdx 결정
else {  # LPS가 발생했을 경우
	if ( pStateIdx == 0 )  # LPS의 확률이 0.5인 경우
    	valMPS = 1 - valMPS  # MPS와 LPS를 바꿔줌
    pStateIdx = transIdxLPS ( pStateIdx ) # 아래 table을 보고 pStateIdx 결정
}

VVC CABAC

HEVC CABAC에 비해 주요한 변화들

CABAC Core Engine

• HEVC의 CABAC은 심볼 확률 예측에 많은 실험을 통해 결정
• Multi-hypthesis probability estimation(다중 가설 확률 추정)
  • 여러 가지 가설을 기반으로 LPS 확률을 추정하는 것이 더 이득

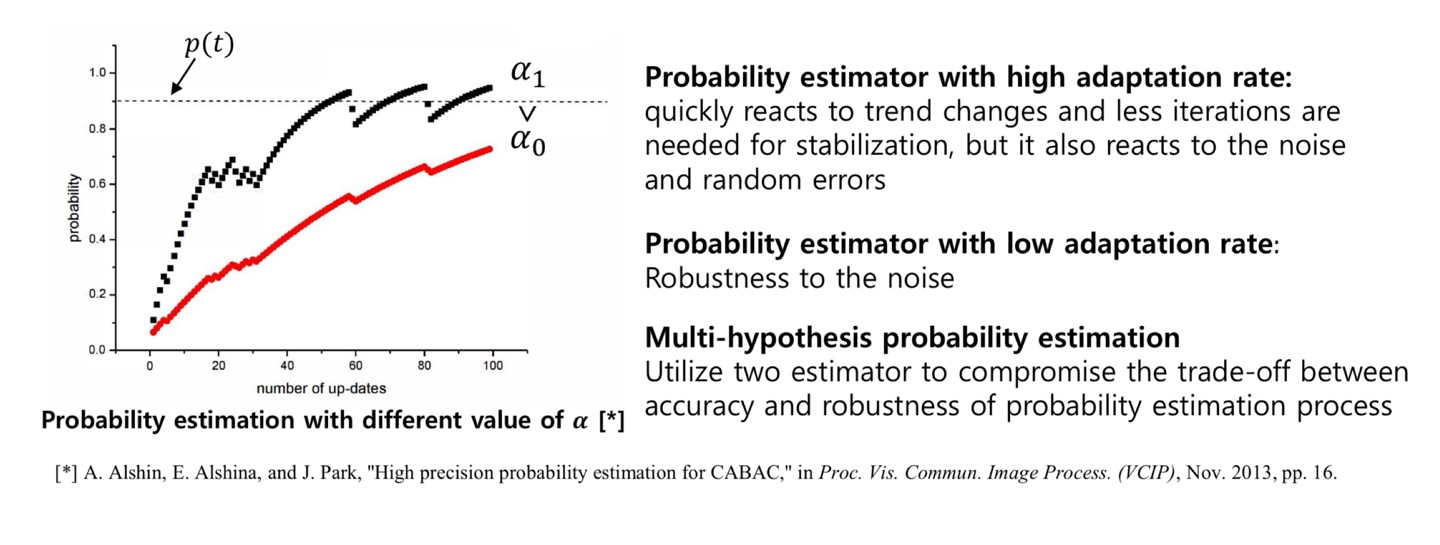
• 검은색 그래프를 보면, MPS가 발생했을 때 증가하고 LPS가 발생했을 때 감소
  • 그래프의 증가폭을 어떻게 설정하는 것이 좋을까에 대한 기술
• High Adaptation Rate (검은색 그래프)
  • 변화에 빨리 적응하여 성능이 빨리 좋아지는 장점
  • Noise에 취약하다는 단점
• Low Adaptation Rate (붉은색 그래프)
  • 변화에 느리게 적응하지만 Noise에 강인
• Multi-hypothesis probability estimation
  • 두 개 다 사용
  • 정확도와 강인함 사이의 Trade-off를 비교하여 결정

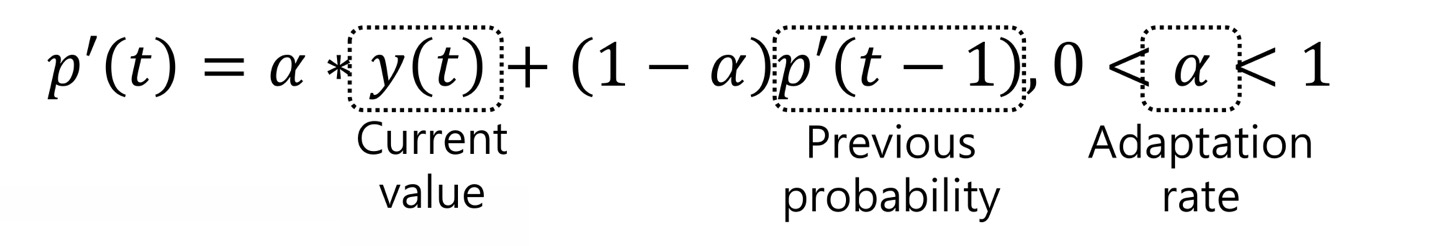
• MPS 확률 계산
  • a0 : Low Adaptation Rate의 계수
  • a1 : High Adaptation Rate의 계수
• a0는 항상 a1보다 큼
• 어떤 계수를 선택할건지는 Syntax Element 별로 다르게 사용

Transform Coefficient Level Coding

• Transform Coefficient Coding 하는 데에 있어서 Context Coded Bin(CCB)의 최대 개수를 제한
  • 속도를 증가시키기 위해

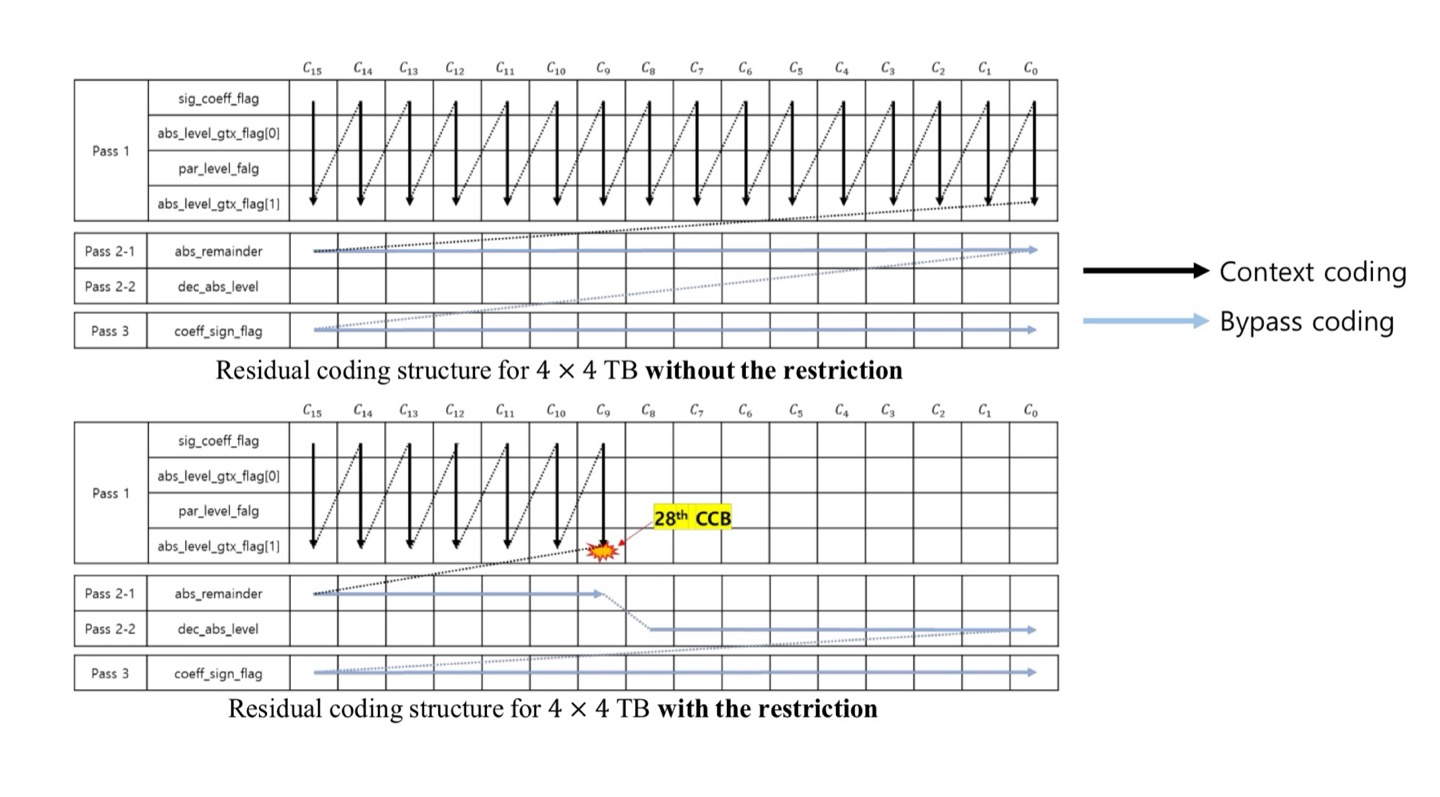
• Syntax Element에 대해서 DCT Coefficient를 Zig-Zag로 스캔하여 Context Codig을 수행
• CABAC으로 압축해도 이득이 없는 경우 Bypass Coding을 수행
• 아래 조건을 만족하면 Context Coding이 아닌 Context Coding을 수행
  • Maximum number of CCB for Luma > TB_zosize * 1.75
  • Maximum number of CCB for Luma > TB_zosize * 1.25
• CCB의 개수가 조건보다 많아지게 되면 Bypass로 전송하는 것이 속도면에서 이득

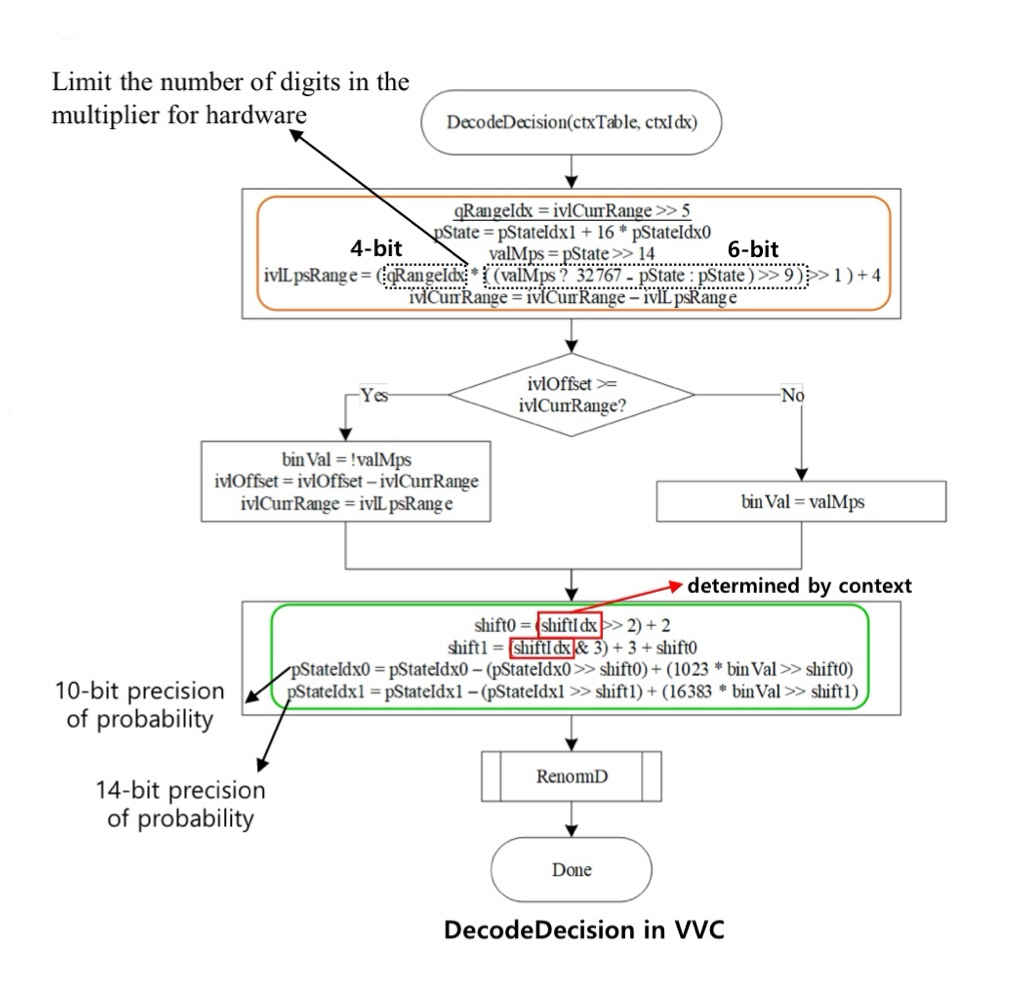
곱셈기로 MPS, LPS의 확률 계산

• 기존 HEVC CABAC에서는 계산량을 줄이기 위해 Table 방식으로 CABAC을 구현
  • 예 : pState Index Table
  • 곱셈을 사용하지 않음
• VVC CABAC에서는 Table 방식을 사용하지 않음
  • 곱셈기를 이용해 MPS, LPS의 확률을 계산
• 실험 결과, Table을 만드는 것이 Cost와 Cycle 면에서 손해라는 것을 확인

HEVC와 VVC의 CABAC 비교

• HEVC CABAC
  

• VVC CABAC

  • Bit Range
    • ivlLpsRange, ivlCurrRange : 9-bit
    • qRangeIdx : 4-bit
    • pState : 15-bit

출처 및 참조

• MPEG뉴미디어포럼/한국방송∙미디어공학회 2023 Summer School
• 심동규, IMAGE PROCESSING SYSTEMS LABORATORY, 강원대학교