Loss Functions(손실함수)

• 어떤 W(가중치)가 가장 좋은지를 결정하기 위해서 지금 만든 W가 좋은지 나쁜지를 정량화할 방법이 필요하다
• 손실함수는 W를 입력으로 받아서 각 스코어를 확인하고 이 W가 지금 얼마나 별로인지를 정량적으로 말해주는 역할을 한다
• 정확하게 말하자면 손실함수는 머신러닝 또는 딥러닝 모델의 예측 결과가 실제 값과 얼마나 차이가 나는지를 측정하는 함수이다. 이를 통해 모델의 성능을 평가하고, 모델을 학습시키는 데 사용한다
• 손실 함수의 값이 낮을수록 모델의 예측 결과가 실제 값과 가까워진다
• 따라서, 모델을 학습시킬 때는 손실 함수의 값을 최소화하는 방향으로 파라미터를 업데이트하게 된다
• 회귀 문제에서는 평균 제곱 오차(Mean Squared Error, MSE)를, 분류 문제에서는 교차 엔트로피(Cross-Entropy)를 주로 사용한다

손실함수의 일반적인 공식

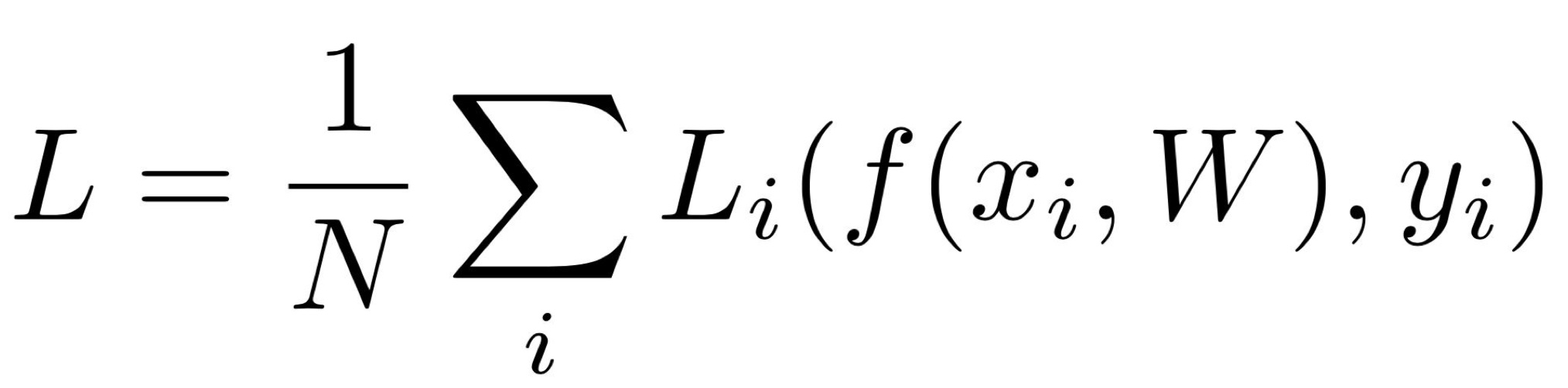
• X, Y : 트레이닝 데이터
• X : 알고리즘 입력
• Y : 레이블 or 타겟
  • 보통 1 ~ 10 사이의 숫자를 가진다
  • 각 1 ~ 10의 숫자 : 각 이미지 X의 정답 카테고리
• f(x, W) : 함수
• L_i : 손실함수
• N : 샘플들의 개수
• L : 데이터 셋에서 각 N개의 데이터 샘플들의 Loss 평균

Multi-class SVM loss

• SVM 알고리즘을 여러 클래스의 분류 문제에 적용할 때 사용하는 손실 함수
• 각 클래스에 대한 점수를 계산하고, 실제 클래스의 점수가 다른 클래스의 점수보다 일정 마진 이상 높아지도록 한다. 이를 통해 각 데이터 포인트가 실제로 속한 클래스를 정확하게 예측하도록 모델을 학습시킨다
• L_i = Σ_j≠y_i max(0, s_j - s_yi + Δ)
  • L_i : i번째 데이터 포인트에 대한 손실
  • s_j : j번째 클래스에 대한 점수
  • s_yi는 실제 클래스에 대한 점수
  • Δ : 마진
  • 계산과정에서 상쇄되기에 마진의 크기를 결정하는 것은 큰 의미가 없다
• 손실 함수의 값이 0보다 크면, 즉 실제 클래스의 점수가 다른 클래스의 점수보다 Δ만큼 높지 않으면 손실이 발생하게 된다
• 이 손실을 최소화하는 방향으로 모델을 학습시키면, 각 데이터 포인트가 실제로 속한 클래스를 정확하게 예측하는 모델을 얻을 수 있다

설명

• L_i를 구하기 위해 우선 "True인 카테고리" 를 제외한 "나머지 카테고리 Y"의 합을 구한다. 다시말해 정답이 아닌 카테고리를 전부 합치는 것이다
• 그리고 올바른 카테고리의 스코어와 올바르지 않은 카테고리의 스코어를 비교해 본다
• 만약 올바른 카테고리의 점수가 올바르지 않은 카테고리의 점수보다 더 높으면, 그리고 그 격차가 일정 마진(safety margin) 이상이라면(위 예시에서는 그 마진을 1로 두었다), 이 경우는 True인 스코어가 다른 false 카테고리보다 훨씬 더 크다는 것을 의미하게 된다
• 그렇게 되면 Loss는 0이 된다
• 이미지 내 정답이 아닌 카테고리의 모든 값들을 합치면 그 값이 바로 한 이미지의 최종 Loss 가 되는 것이다
• 그리고 전체 트레이닝 데이터 셋에서 그 Loss들의 평균을 구한다
• 평균값은 분류기가 얼마나 안 좋게 분류하고 있는지의 "정량적 지표"가 된다

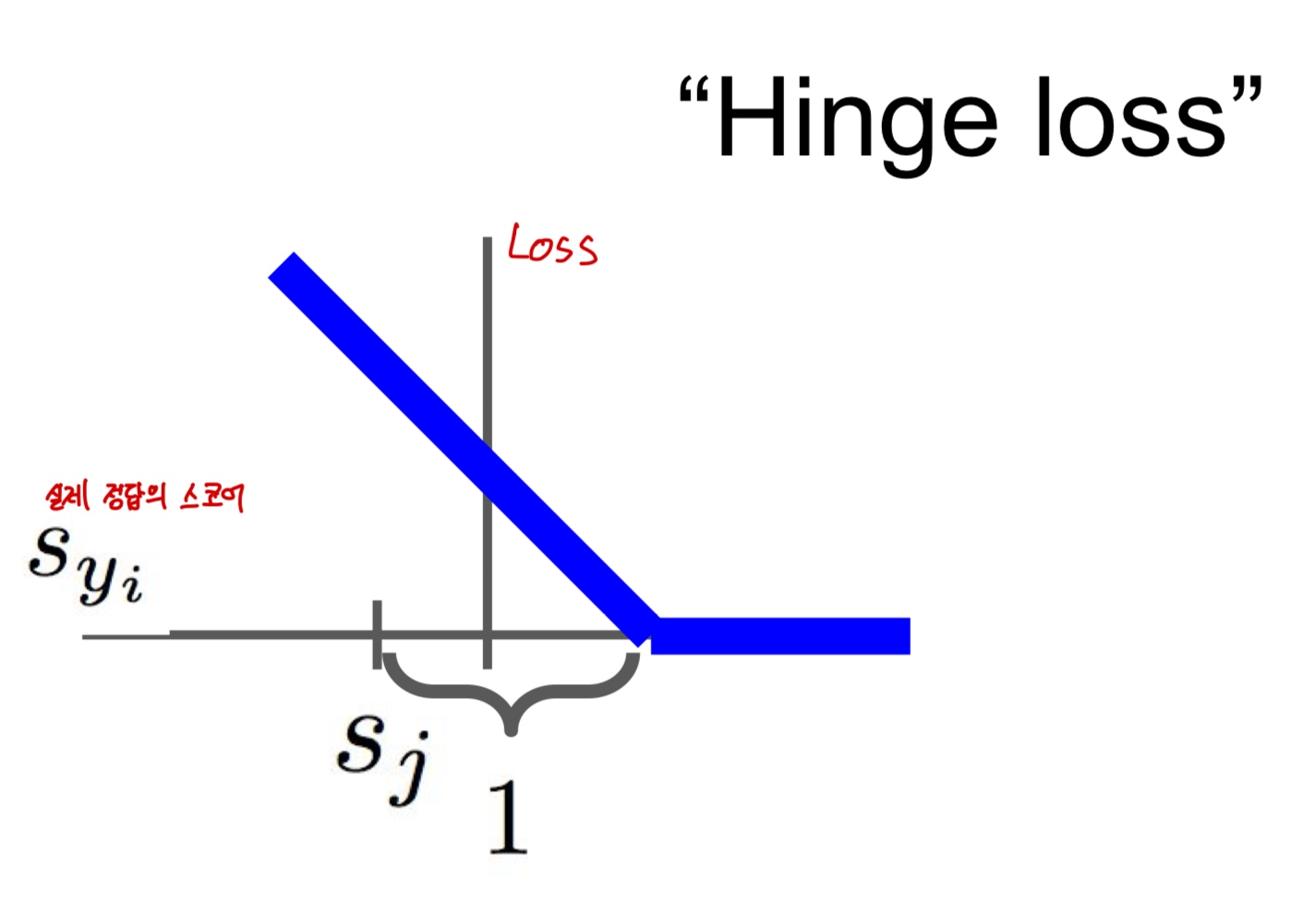
Hinge loss

• 이 손실 함수는 실제 클래스와 예측 클래스 간의 마진을 최대화하는 방향으로 모델을 학습시킨다
  -다중 클래스 SVM에서의 힌지 손실은 각 클래스에 대한 점수를 계산하고, 실제 클래스의 점수가 다른 클래스의 점수보다 일정 마진 이상 높게 나오도록 한다. 이 마진이 충족되지 않는 경우에만 손실이 발생한다
• 정답 카테고리의 점수가 올라갈수록 Loss가 선형적으로 줄어드는 것을 알 수 있다
• 이 로스는 0이 된 이후에도 Safety margin을 넘어설 때 까지 더 줄어든다
• Loss가 0이 됐다는 건 클래스를 잘 분류했다는 뜻이다
• 다중 클래스 SVM에서의 힌지 손실을 최소화하면, 모델은 각 데이터 포인트에 대해 실제 클래스의 점수가 다른 클래스의 점수보다 적어도 Δ만큼 높게 나오도록 학습된다

Regularization

• 과대적합(Overfitting)을 방지하고 일반화 성능을 향상시키기 위한 기법
• 모델의 복잡도를 제한하여 학습 데이터에 너무 맞춰져서 새로운 데이터에 대한 예측 성능이 떨어지는 현상을 방지한다
• 정규화는 손실 함수에 항을 추가함으로써 이루어진다. 이 항은 모델의 가중치 크기에 대한 패널티를 나타내며, 주로 L1 정규화와 L2 정규화 두 가지 형태가 있다

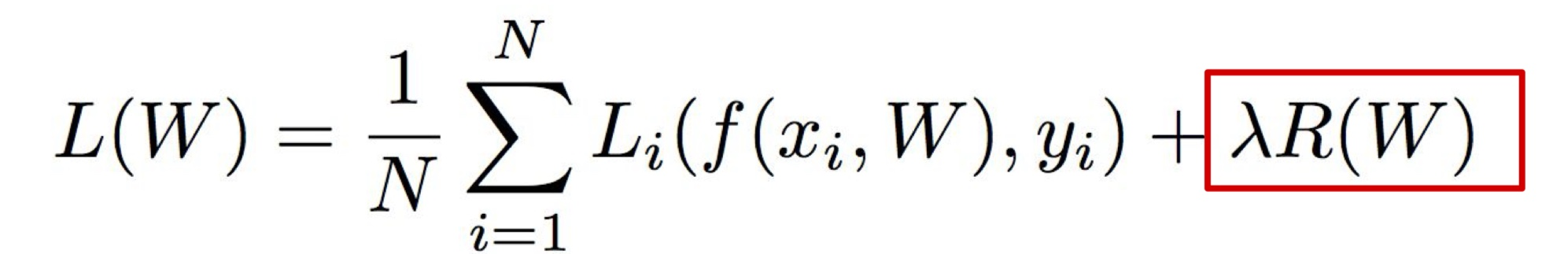
Regularization의 종류

• L2 regularization
• 가중치 행렬 W에 대한 Euclidean Norm에 패널티를 주는 것
• L1 regularization
  • L1 norm으로 가중치 행렬 W에 패널티를 부과하는 것
  • L1 regularization을 하면 행렬 W가 희소행렬이 되도록 한다
• Elastic net regularization
  • L1과 L2를 섞은 것
• Max norm regularization
  • L1, L2 대신에 max norm을 쓰는 것
• Drop out
• Batch normalization
• stochastic depth

Multinomial logistic regression(softmax loss)

• 각 클래스에 대한 확률을 계산하고, 가장 확률이 높은 클래스를 선택하여 분류를 수행한다
• softmax loss를 사용하여 각 클래스에 대한 점수를 확률로 변환한다
• Softmax function
  • P(y = i|X) = exp(xi) / ∑(exp(xj))
  • xi : i 클래스에 대한 점수
  • ∑(exp(xj)) : 모든 클래스의 점수에 대한 지수 함수의 합
• 이렇게 계산된 확률은 모두 0과 1 사이의 값을 가지며, 모든 클래스에 대한 확률의 합은 1이 된다
• Softmax loss
  • L = -log(P(y = i|X))
  • P(y = i|X) : 실제 클래스 i에 대한 확률
  • P(y = i|X) 확률이 높아질수록 손실은 작아지므로, 모델은 손실을 최소화하도록 학습된다
• 위 수식을 이용해서 스코어를 가지고 클래스 별 확률 분포를 계산하게 된다

SVM과 Softmax의 차이

• SVM의 경우에는 일정 선(margins)을 넘기만 하면 더이상 성능 개선에 신경쓰지 않는다. 반면 softmax는 더더더더더좋게 성능을 높이려 한다
• SVM
  • 이진 분류 문제에 주로 사용되는 알고리즘
  • SVM은 데이터를 고차원 공간에 투영하여 두 클래스 간의 마진(즉, 두 클래스를 구분하는 경계와 각 클래스의 가장 가까운 데이터 포인트 사이의 거리)을 최대화하는 초평면을 찾는다
  • SVM은 이진 분류에 매우 효과적이지만, 다중 클래스 분류를 위해서는 일대다(one-vs-all) 또는 일대일(one-vs-one) 같은 전략을 사용해야 한다
• Softmax
  • 다중 클래스 분류 문제에 주로 사용
  • 각 클래스에 대한 점수를 계산한 후, 소프트맥스 함수를 통해 이를 확률로 변환
  • 이 확률은 각 데이터 포인트가 각 클래스에 속할 확률을 나타내며, 가장 높은 확률을 가진 클래스가 예측 결과가 된다
  • 소프트맥스는 다중 클래스 분류 문제를 직접적으로 다룰 수 있어 편리하다

Optimization(최적화)

Random search(임의 탐색)

• 임의로 샘플링한 W들을 엄청 많이 모아놓고 Loss를 계산해서 어떤 W가 좋은지를 살펴보는 것
• 간단하고 쉽게 구현할 수 있지만 성능이 매우 안 좋으므로 사용하지 않는 것이 좋다

Local getometry

• 지역적인 기하학적 특성을 이용
• 이는 주어진 지점 주변의 기울기(Gradient)나 곡률(Hessian) 행렬 등을 통해 파악할 수 있다
• 기울기는 최적화 알고리즘이 '가장 급격하게 증가하는 방향'을 찾는 데 사용된다
• 헤시안 행렬은 함수의 두 번째 도함수를 나타내며, 문제 공간의 곡률을 설명하는 데 사용된다
• Local getometry는 최적화 알고리즘의 성능을 크게 영향을 미친다
• 문제 공간이 매우 복잡하거나 곡률이 크면, 그래디언트 기반의 최적화 알고리즘은 지역 최적점(Local Optimum)에 갇히거나, 최적점을 찾는 데 오랜 시간이 걸릴 수 있다

Gradient

• 주어진 지점에서 함수의 변화율을 의미
• 특정 지점에서 함수의 값이 얼마나 빠르게 증가하거나 감소하는지를 나타내는 지표
• Gradient는 최적화 알고리즘에서 매우 중요한 역할을 한다
  • 기울기가 양수인 경우, 해당 방향으로 움직이면 함수의 값이 증가한다
  • 기울기가 음수인 경우 함수의 값이 감소한다
• 다변수 함수에서는 각 변수 방향의 기울기를 벡터로 나타낸 것을 말한다
• gradient의 방향 : 함수에서 가장 많이 올라가는 방향
• 함수의 어던 점에서의 선형 1차근사 함수를 알려주기에 중요하다

경사하강법(Gradient Descent)

• 최적화 알고리즘 중 하나로, 함수의 최소값을 찾는 데 사용된다
• 현재 위치에서의 기울기(그래디언트)를 계산하고, 그 기울기가 가장 크게 감소하는 방향으로 조금씩 이동하면서 최소값을 찾는다
• 알고리즘
  • 초기값 설정 : 매개변수의 초기값을 설정
    • 이 값은 무작위로 설정하거나 사전에 알려진 좋은 값으로 설정 가능
  • 기울기 계산 : 현재 매개변수 값에서의 함수의 기울기를 계산
  • 매개변수 업데이트: 계산한 기울기와 학습률(learning rate)을 곱한 값을 현재 매개변수 값에서 빼서 매개변수를 업데이트
    • 이 때, 학습률은 매개변수가 얼마나 빠르게 업데이트되는지를 결정하는 매개변수이다
  • 반복 : 위 과정을 최소값에 도달할 때까지 또는 미리 정한 횟수만큼 반복한다
• 주의할 점
  • 학습률이 너무 크면 최소값을 찾지 못하고 발산할 수 있다
  • 학습률이 너무 작으면 최소값을 찾는 데 시간이 오래 걸릴 수 있다
  • 지역 최소값(local minimum)에 빠져 전역 최소값(global minimum)을 찾지 못할 수 있다

Stochastic Gradient Descent(SGD)

• 확률적 경사 하강법은 최적화 문제를 해결하기 위한 방법 중 하나이다
• 일반적인 경사 하강법이 모든 데이터 셋에 대한 오차를 계산하여 경사를 구하는 데 반해, SGD는 랜덤하게 선택한 하나의 데이터에 대해서만 오차를 계산하고 경사를 구한다
• 전체 데이터 셋의 gradient과 loss를 계산을 하면 계산량이 어마하게 많아 시간이 오래걸린다. 이를 해결하기 위해, 전체 데이터 셋의 gradient과 loss를 계산하기 보다는 Minibatch라는 작은 트레이닝 샘플 집합으로 나눠서 학습하는 방법이다
• Minibatch는 보통 2의 승수로 정하며 32, 64, 128을 보통 사용한다
• 따라서 이 작은 minibatch를 이용해서 Loss의 전체 합의 "추정치"와 실제 gradient의 "추정치"를 계산한다
• 장점
  • 계산 효율성
    • 한 번의 반복에서 하나의 데이터만을 처리하기 때문에, 대량의 데이터를 다루는 머신러닝에서는 SGD가 훨씬 빠른 속도로 학습이 가능하다
  • 데이터의 불규칙성 활용
    • 랜덤하게 데이터를 선택하기 때문에, SGD는 데이터의 불규칙성을 활용하여 지역 최적해(Local Optima)에 빠지는 것을 피할 수 있다
  • 온라인 학습 가능
    • 데이터가 순차적으로 들어오는 온라인 학습 상황에서도 SGD는 적용이 가능하다

이미지 특징

• 영상 자체를 입력으로 사용하는 것은 성능이 좋지 않다
• 그래서 DNN이 유행하기 전에 주로 쓰는 방법은 두가지 스테이지를 거치는 방법이다
  • 첫 번째는, 이미지가 있으면 여러가지 특징 표현을 계산하는 스테이지이다
  • 두 번째는, 여러 특징 표현들은 한데 연결시켜(Concat) 하나의 특징 벡터로 만드는 스테이지이다

Color Histogram

• 이미지의 컬러 분포를 시각적으로 표현한 것
• 이미지에서 각각의 Hue 값에 대한 픽셀의 빈도수를 나타낸다
• 이미지의 전반적인 컬러 분포를 파악하는 데 유용하며, 특히 색상이 중요한 이미지 검색, 이미지 분류 등의 작업에서 효과적으로 사용될 수 있다

Histogram of Oriented Gradients(HoG)

• 이미지의 지역적인 그래디언트 방향을 히스토그램으로 표현한 특징
• Local orientation edges를 측정
• 이미지 내에 전반적으로 어떤 종류의 edge정보가 있는지를 나타낸다
• 이미지를 여러 부분으로 지역화해서, 지역적으로 어떤 edge가 존재하는지도 알 수 있다
• 단계
  • 그래디언트 계산
    • 먼저, 이미지의 각 픽셀에서 그래디언트(밝기의 변화)를 계산한다
    • 이는 보통 소벨 필터(Sobel filter) 등의 에지 감지 필터를 사용한다
  • 셀로 분할
    • 그 다음, 이미지를 겹치는 작은 사각형 영역(셀)으로 분할한다
    • 각 셀은 보통 6x6, 8x8, 16x16 등의 크기를 가진다
  • 히스토그램 생성
    • 각 셀에서 그래디언트 방향의 히스토그램을 생성한다
    • 이때, 그래디언트 방향은 보통 0도부터 360도 또는 0도부터 180도의 범위를 가진다
  • 정규화
    • 마지막으로, 히스토그램을 정규화하여 조명의 변화에 대한 영향을 줄인다
    • 이는 보통 셀을 더 큰 블록으로 그룹화하고, 각 블록 내에서 히스토그램을 정규화하는 방식으로 이루어 진다

Bag of Words

• 자연어 처리(Natural Language Processing, NLP)에서 텍스트 데이터를 표현하는 기본적인 방법 중 하나이다
• 어떤 문장이 있고, BOW에서 이 문장을 표현하는 방법은 바로 문장의 여러 단어의 발생 빈도를 세어서 특징 벡터로 사용하는 것이다. 하지만 BOW를 이미지에 적용하는 것은 쉬운 문제가 아니였다
• 이를 해결하기 위해 "시각 단어(visual words)"라는 것을 새로 정의했다. 여기에서는 2단계의 과정이 있다
• 엄청 많은 이미지를 가지고, 그 이미지들은 임의대로 조각낸다. 그리고 그 조각들을 K-means와 같은 알고리즘으로 군집화 한다. 이미지 내의 다양한 것들을 표현할 수 있는 다양한 군집들을 만들어 내는 것이다
• 군집화 단계를 거치고나면, 시각 단어(visual words)는 빨간색, 파랑색, 노랑색과 같은 다양한 색을 포착해낸다. 뿐만 아니라 다양한 종류의 다양한 방향의 oriented edges또한 포착할 수 있다
• 이런 시각 단어(visual words) 집합인 Codebook을 만들고 어떤 이미지가 있을 때, 이 이미지에서의 시각 단어들의 발생 빈도를 통해서 이미지를 인코딩 할 수 있다. 이는 이 이미지가 어떻게 생겼는지에 대한 다양한 정보를 제공한다

출처 및 참조

https://youtu.be/h7iBpEHGVNc?si=8NWX-Mzv7MkBI_nb