Regression Loss function

• 오늘은 가장 많이 접하는 task인 Regression, 그 중에서도 자주 사용하는 손실함수에 대해 정리하고자 한다.

  • Mean_Squared_Error
  • Mean_Absolute_Error
  • Huber Loss
  • Smooth L1 Loss
  • Symmetric_Absolute_Percentage_Error

1. MSE(Mean_Squared_Error)

• 회귀 Task에서는 보통 Mean Squared Error, Mean absolute Error, 이외에 MSE의 제곱근을 사용하는 RMSE, MAPE 등 다양한 손실함수가 사용된다.

• MSE(= L2 Loss)
  예측 값과 실제 값 차이의 제곱한 값을 사용하며, 식은 아래와 같다.

  $MSE = \frac{1}{N}\sum^N_{n=1}(y-\hat{y})^2$

• MSE는 빠른 수렴으로 많이 사용

• 하지만 이상치에 민감하여 이상치가 많은 경우 다른 손실함수를 사용해야한다.

2. MAE(Mean_Absolute_Error)

• MAE는 예측 오차를 선형 처리하여 이상치에 강건하고, 단순 차이 값이기 때문에 결과 해석이 직관적인 특징을 갖는다.

• MAE(= L1 loss)

  $MAE = \frac{1}{N}\sum^N_{n=1}|(y-\hat{y})|$

• 그레디언트 부호만 다르고 항상 동일한 크기를 가짐(sign-dependent)

  • MAE는 미분 시 +1, -1 처럼 부호만 다를뿐 크기는 동일

• 이상치, 노이즈에 강건한 특성

  • 평균을 예측하는 MSE와 다르게, MAE는 분포의 중앙값(median)을 예측하기 때문에 이상치에 강건

3. Huber Loss

• MSE와 MAE의 절충안인 Huber loss, Smooth L1 loss 등이 사용됨

• Huber loss

  • MSE와 MAE의 각 장점을 사용하는 손실함수
  • delta가 손실함수에 사용되는데, 이 delta로 두 손실함수 중 어떤 함수를 사용할지 판단하는 기준으로 사용된다.
  • 수식은 아래와 같다.
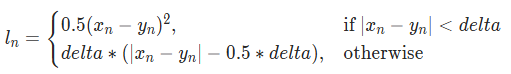    값의 차이가 delta보다 작으면 L2 구간이라하여 MSE를 사용하고, 반대로 delta보다 이상이면 L1 구간이라하여 MAE 손실을 사용한다.
  • 즉, 오차가 작은 구간에서는 MSE를 사용하여 0 근처에서 첨점으로 인해 미분이 어려운 MAE의 단점을 해결하고, 오차가 큰 구간에서는 MAE를 사용하여 이상치에 강건하도록한 손실
  • delta가 파라미터로 쓰이며, 당연히 적절한 delta를 찾는 게 중요!

4. Smooth L1 loss

• Huber loss와 유사한 손실로, 매커니즘은 동일하지만 실제 손실에 곱해지는 값이 다르다.
• Huber loss의 delta = Smooth L1 loss의 beta
• 수식은 아래와 같다.
  
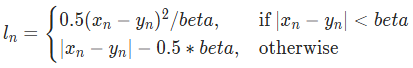
• Fast R-CNN에서는 Smooth L1 Loss를 사용하여 기울기 폭발(gradient exploding) 방지
  • MSE는 학습 과정 중 손실을 미분하여 파라미터의 업데이트 기울기가 결정된다.
  • 손실 값이 커지는 경우 기울기 폭발이 발생할 수 있지만 Smooth L1 loss는 실제 값을 beta로 나누는 과정을 통해 기울기 폭발을 방지한다.

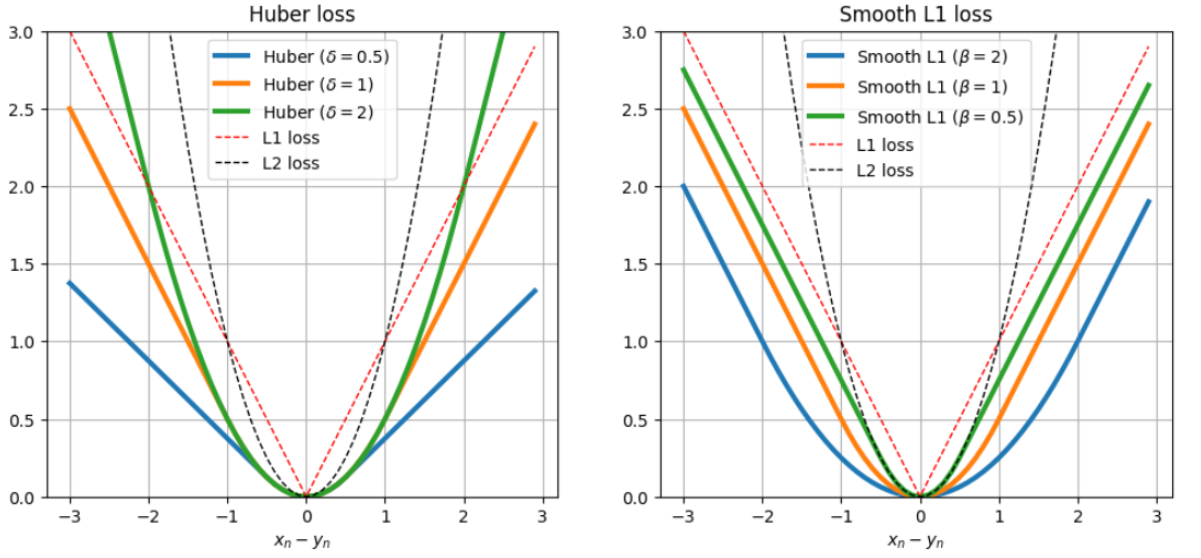
• 위 그림은 각 손실의 delta, beta 값에 따라 시각화한 결과로, delta와 beta 모두 1인 경우에는 동일한 함수임을 알 수 있다.

• Huber loss의 경우 delta가 커지면 2차 함수 형태에 가까워지고, 작아지면 1차식 형태에 가까워진다.

• Smooth L1 loss의 경우는 beta가 1보다 커지면 MSE 구간이 넓어지고, 1보다 작아지는 경우 MAE의 구간이 넓어진다.

5. SMAPE(Symmetric Absolute Percentage Error)

• 0~200사이의 값을 갖는 지표로, MAPE의 단점을 보완한 손실로, MAPE와 직접적인 차이는 예측한 값의 절대값도 손실 계산에 포함한다는 것이다.

  • MAPE는 |실제 값|만 분모에 사용

• SMAPE의 수식은 아래와 같다.

  $SMAPE = \frac{1}{N}\sum_{n=1}^{N}{\frac{|True - prediction|}{(|True| + |Prediction|) / 2}}$

• MAPE는 같은 손실 값이어도 |실제 값|으로만 분모를 구성하여 실제로 동일한 차이도 다르게 계산될 수 있다. 물론 실제 값이 충분히 큰 수라면 문제가 안 되지만, 실제 값이 작은 경우 해당 손실은 무한대로 발산할 수 있어, 실제 값이 작은 경우 MAPE는 적절한 손실로 사용하기 어렵다.

• 반면, SMAPE는 |예측 값|도 분모에 포함하여 MAPE에 비해 공정하게 평가할 수 있다.

• SMAPE 구현 코드

def SMAPE(preds, trues, eps = 1e-8):
	
    numerator = np.abs(trues - preds)
    denominator = np.abd(trues) + np.abs(preds) + eps
    smape = 2.0 * numerator / denominator
    
    return np.mean(smape)