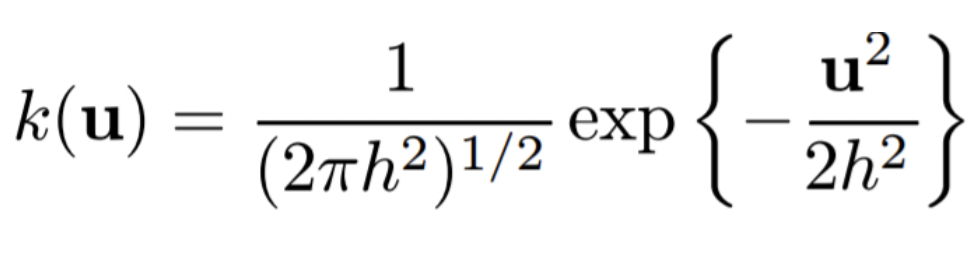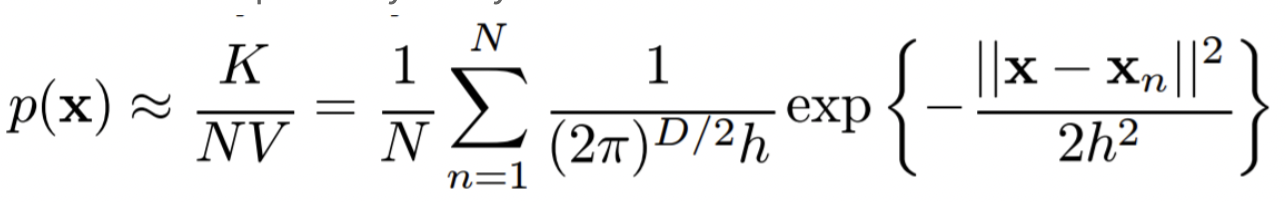GLocal-K: Global and Local Kernels for Recommender Systems

논문 직접 구현해보기!!

논문 선정 이유

Recommendation 분야의 논문을 한 번 읽어보고 싶었다. sota 논문이다.

관련 내용 정리

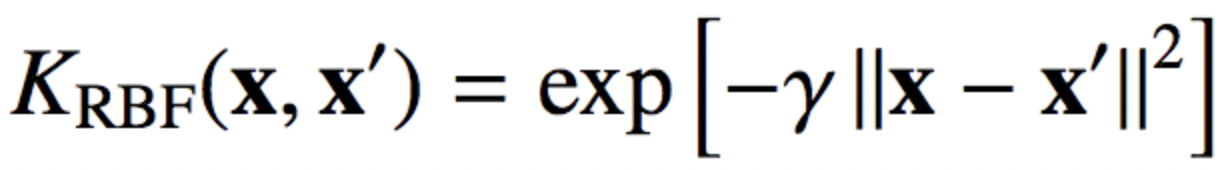
• 2d-RBF kernel

• Kernel methods

  • 데이터의 분포를 파악하는 것은 머신러닝의 중요한 문제이나, 우리는 이를 쉽게 알 수 없다. 데이터의 분포를 추정하여 확률 분포를 추정하는 방법에는 histogram, kernel density estimation(kernel method), K-nearest neighbor 등 다양한 방법이 있다.

  • 확률 밀도 p(x)
    

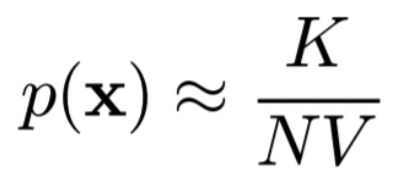
  • 위 식에서 N은 전체 데이터의 수(constant), K는 해당 region 안의 데이터 수, V는 해당 region의 부피이다. V를 고정하는 것이 kernel method, K를 고정하는 것이 KNN 방법이다.

  • Parzen Window
    

    • 

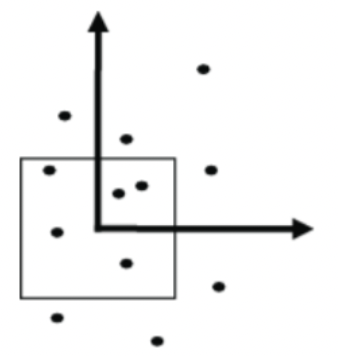
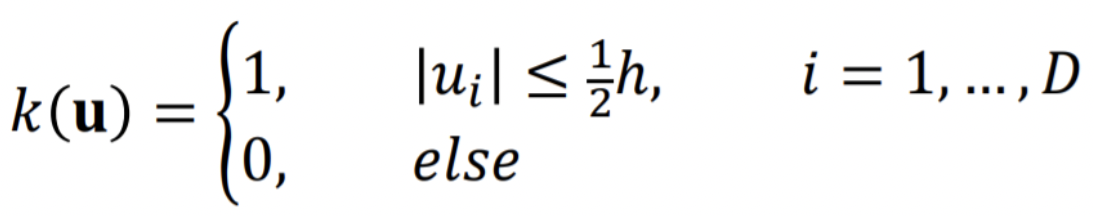
    • 위 식을 data point u의 kernel function이라고 한다. 이 kernel function으로 K, V를 아래와 같이 나타낼 수 있다.

    • 

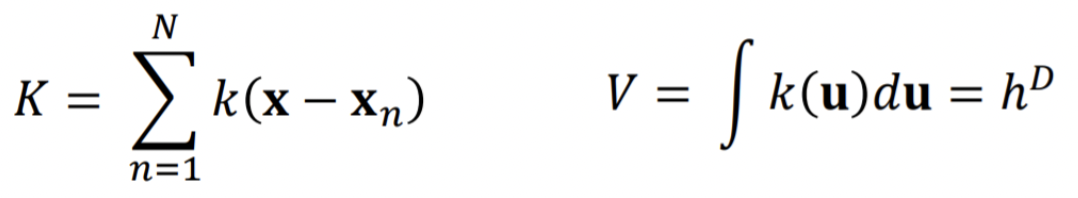
    • 이를 바탕으로 확률 밀도 p(x)는 아래와 같이 구할 수 있다.

    • 

    • 그러나 parzen window 방식은 각 cube의 경계 값 위에 데이터가 있을 때 이를 처리하는 것이 모호하다(discontinuity)는 단점을 가짐. 때문에 Gaussian kernel을 사용함.

  • Gaussian kernel

    • 

    • 

    • 

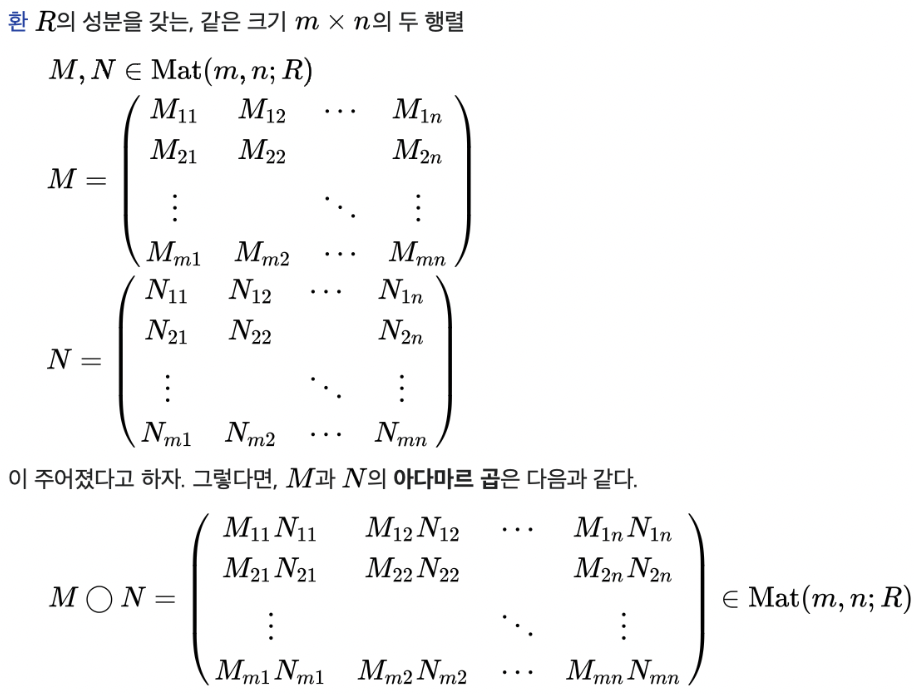
• Hadamard-product

  • 

Abstract

• Recommender sys는 보통 고차원 sparse use-item matrices에서 수행된다. Matrix completion은 각각 수천개의 item subset을 가진 수백만명의 user 기반으로 interest를 예측하는 task이다.
• Global Local Kernel-based matrix completion framework 제안.
  • 고차원 sparse use-item matrix entry를 저차원의 적은 중요 feature 행렬로 변환하고 일반화함.
  • 2가지 단계로 이뤄짐.
    1. 2d-RBF kernel로 data를 1 space에서 feature space로 변환하는 local kernelised weight matrix로 auto encoder를 pretrain함.
    2. pretrained된 auto encoder를 각 item의 charateristic을 추출하는 convolution-based global kernel로 만들어진 rating matrix로 fine-tuning함.
• user-item rating matrix만 포함하는 extreme low-resource setting에서 GLocal-K를 적용하여 sota 달성함.

CCS Concepts

• Information systems -> Recommender systems;
• Theory of computation -> Kernel methods

| Keywords

• Recomender systems, Matrix completion, Kernel methods

I. Introduction

• Collaborative filtering-based recommender system : 다른 많은 user의 preference를 바탕으로 해당 유저의 interest를 예측

• 주요 접근법: Matrix Completion

  • 각 행과 열은 user와 item을 나타냄. user의 rating을 예측하는 건 고차원의 user-item rating matrix의 빈 곳을 completion하는 것과 같음. 실제로 이 matrix는 매우 sparse함.
  • Tranditional recommender system은 AE(autoencoder)를 이용하여 고차원 sparse matrix를 저차원 feature space로 변환하는데 집중함. AE는 non-linear user-item relationship을 학습하고 data representation의 complex abstraction을 encoding하는 데에 용이함.
    • I-AutoRec : item-based AE. 고차원 matrix entries를 받아 저차원 latent hidden space로 사영한 후, 다시 고차원으로 복원하여 missing rating을 예측함.
    • SparseFC : finite support kernel를 이용해 weight matrices를 sparsified한 AE를 사용함.
    • GC-MC(이 논문 나중에 읽어보기!!) : graph-based AE 제안. bipartite interaction graph에서 message passing 형식으로(msg passing 형식이 뭘까) user의 latent feature와 item node를 만듦. 이 latent user와 item repr은 bilinear decodr를 통해 rating links를 복구하는데 쓰인다. 이렇게 bipartite graph에서 link prediction을 하는 방식은 side info를 활용하는 쪽으로도 확장 가능.
    • opinion information, attributes of user와 같이 side information을 활용하는 쪽의 연구도 이뤄지고 있으나, 대부분의 실제 상황에서는 side info가 거의 없음.
      -> 우리는 side info 대신 고차원 user-rating matrix를 저차원 latent feature space로 feature extraction하는 데에 집중함.

• 본 연구는 feature extraction에 유용한 2가지 kernel을 소개함.

  • 1) local kernel
    SVM과 함께 많이 쓰임. 고차원으로부터의 data transformation을 수행하여 optimal separating surface를 줌
  • 2) global kernel
    CNN에서 옴. 더 깊고 많은 kernel를 쓸 수록 feature extraction ability를 높일 수 있음.

• Global-Locak Kernel-based matrix completion framework

  • 1) pretraining the AE using local kernelised weight matrix
  • 2) fine-tuning with the global kernel-based rating matrix.

• 본 논문이 기여한 것

  • latent feature를 추출하는 global, local kernel based AE model을 제안
  • recommender system에서 pre-training과 fine-tuning task를 통합함.
  • side info 없이 sota를 달성함.

II. GLOCAL-K

• pre-training - local kernelised weight matrix
  • make dense connections denser and sparse connections sparses using a finite support kernel.
• fine-tuning - global-kernal based matrix.
  • Conv kernel로 data dim을 줄이면서 less redundant하고 적은 수의 important feature set으로 이뤄진 rating matrix 활용.

2.1 Pre-training with local kernel

식 (1)

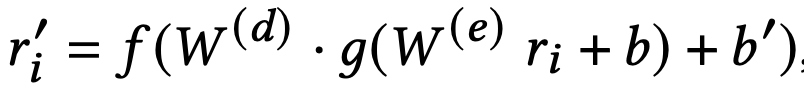
• Auto encoder Pre training
  • item vector r_i를 입력받아 missing ratings를 예측하는 reconstructed vector r_i를 출력함.
  • W^(e), W^(d)는 weight matrices. b in R^h, b' in R^m은 bias vectors. f, g는 non-linear activation funcs.
    
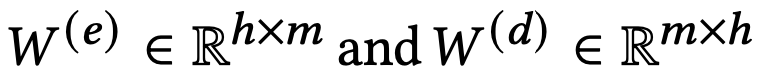
  • AE는 단일 h차원 hidden layer로 된 auto-associative NN를 사용함. dense, sparse connection을 강조하기 위해, AE의 weight matrices를 RBF(radial-basis-function) kernel로 reparameterise함.(Kernel trick)

식 (2)

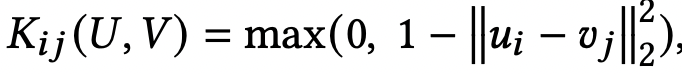
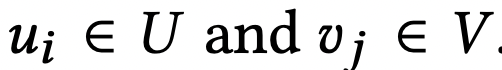
식(3)

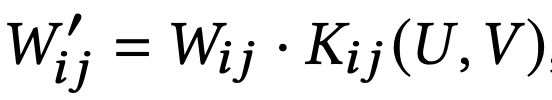
그림 (1)

• Local Kernelised Weight Matrix
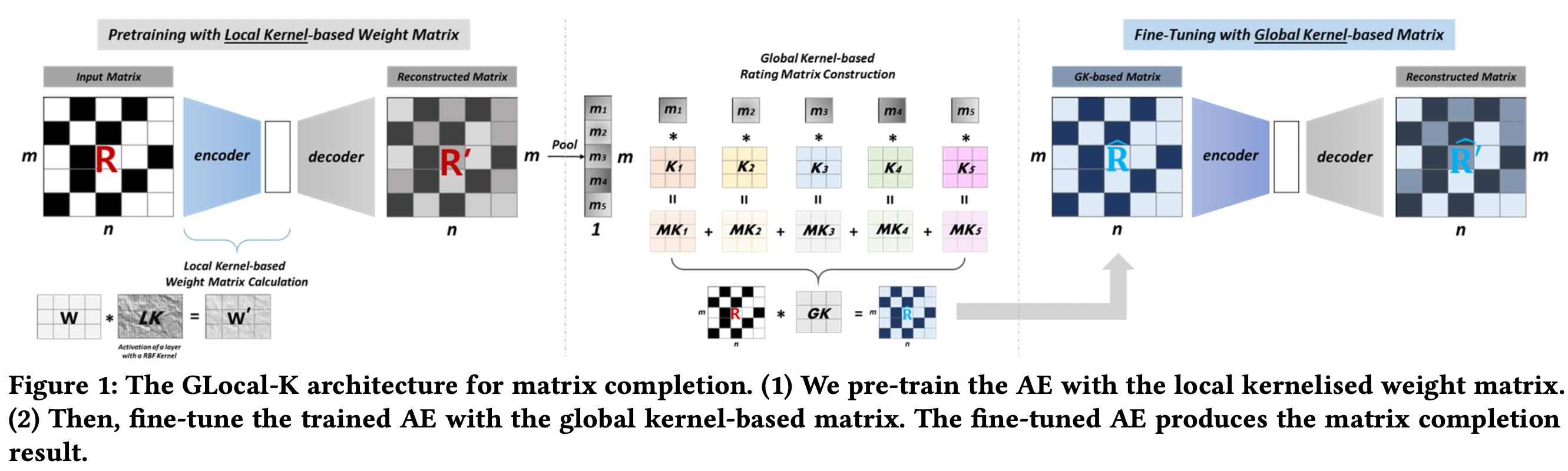
  • 식 (1)의 weight matrices W^(e), W^(d)는 local kernelised weight matrix라고 불리는 2d-RBF kernel로 reparameterised된다.
  • K(.)는 두 벡터 set U, V 간의 similarity를 계산하는 RBF kernel function. kernel function은 LK kernel matrix로 output을 나타낼 수 있다. (??) (LK - 같은 벡터는 1로, 아주 멀리 떨어진 벡터는 0으로 mapping)
  • local kernelizes weight matrix는 식 (3)과 같이 계산된다. 이 때 W'은 sparsified weight matrix를 얻기 위해 weight와 kernel matrices의 Hadamard-product로 계산된다.
  • U, V의 각 vector간 거리가 neural network의 neuron 연결을 결정한다.

2.2 Fine-tuning with Global Kernel

식 (3, 4, 5)

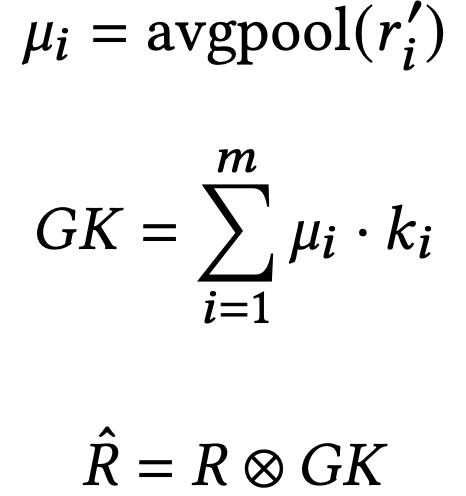
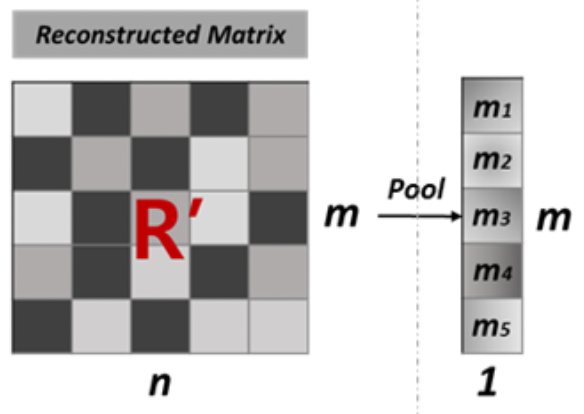
과정 1

과정 2

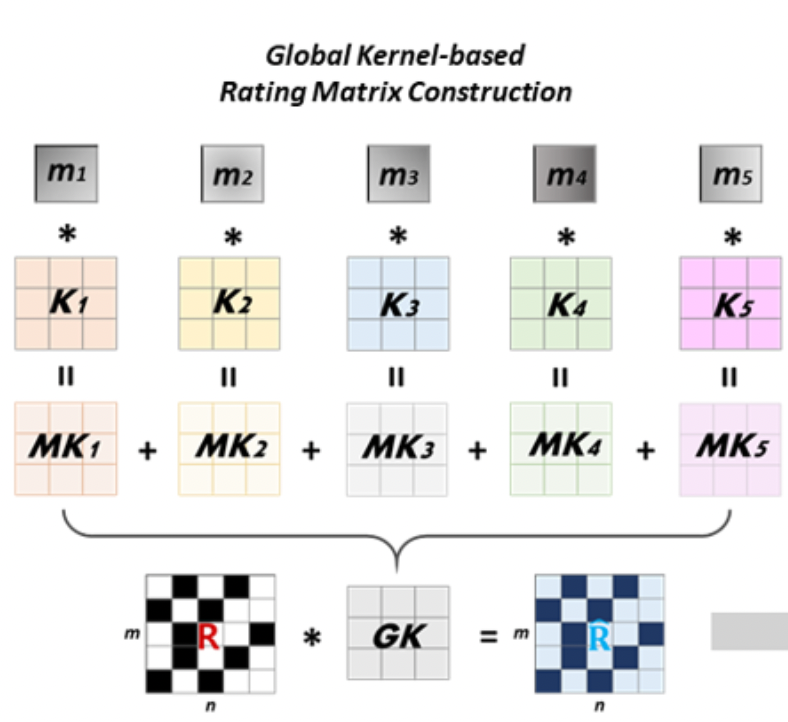
과정 2의 M과 K, GK

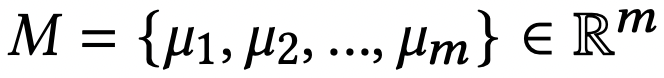
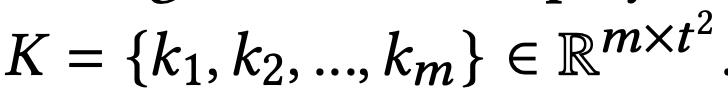
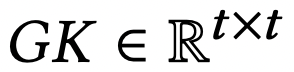
• Global kernel-based Rating Matrix
  • pre-trained auto encoder는 global conv kernel로 만들어진 rating matrix로 fine-tune된다. fine-tuning 이전에, global kernel-based rating matrix를 만들기 위해 global kernel이 어떻게 만들어지는지
  • 과정 1: pre-trained model의 decoder output은 missing entries의 initial predicted ratings을 포함하고, pooling으로 넘겨짐. item-based average pooling으로, rating matrix의 각 item info를 요약할 수 있음.
  • 과정 2: K들은 M과의 내적을 통해 합쳐짐. weight나 rating matrices에 따라 결정되어서 rating-dependent mechanism으로 간주될 수도 있음. 이후 R에 GK로 convolution을 하여 R_hat을 만듦.

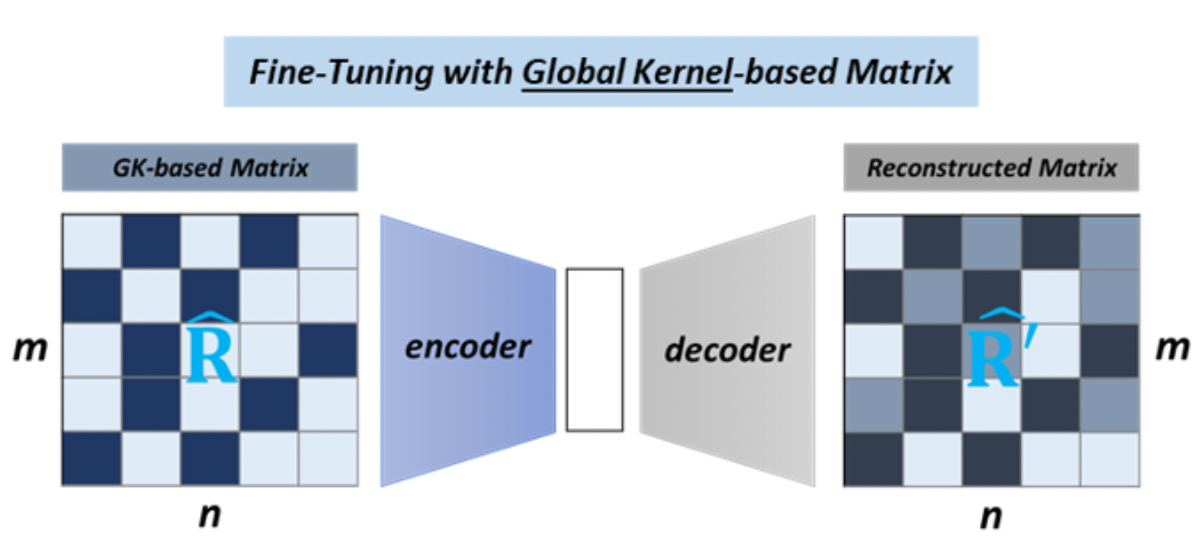
• Auto-Encoder Fine-tuning
  • R_hat을 pre-trained AE model에 넣어서 global kernel-based rating matrix adjustment를 함.