본 논문을 택한 이유
시계열, Audio 데이터 모델에 대해 한 번 이해해보고 싶었다.
개념 정리
Abstract
- Vision Transformer가 성공적으로 적용되면서, signal processing에도 Transformer를 적용해자는 논의가 있었다.
- signal은 보통 Discrete Fourier Transform을 통해 얻은 spectrogram을 이용하는데, 여기에 바로 Transformer를 적용하는 것은 suboptimal하다. Spectogram의 각 축은 보통 frequency와 time 등 다른 차원을 의미하는데, 우리 생각에는 각 축에 대해 나눠서 접근하는 게 더 좋을 것이다.
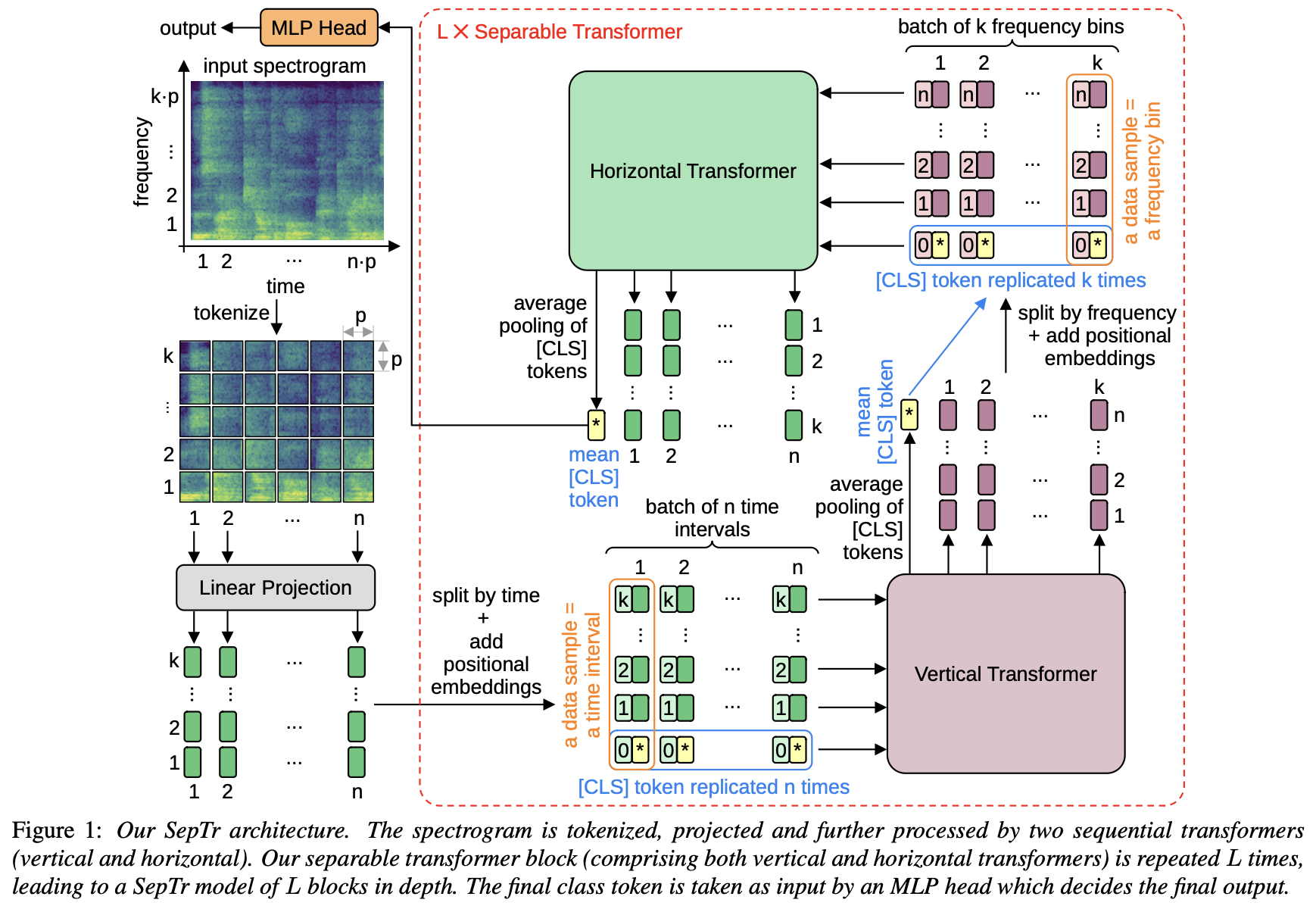
Separable Transformer (SepTr)
- 연달은 2개의 transformer block으로 구성
- 1st block(Vertical Transformer)은 token을 same time interval 내에서 입력받고
- 2nd block(Horizontal Transformer)은 token을 same frequency bin 내에서 입력받음.
I. Introduction
- Gong et al : spectrogram에 ViT를 바로 적용해봄
- time, frequency 양 방향으로 span하는 것은 token 수의 quadratic complexity를 가짐.
- 구현을 쉽게 하기 위해 input spectrogram을 각 축을 따라 batch of data sample로 변환함.
II. Related Work
- Attention, Transformer의 도입
- NLP에서 쓰이던 self-attention mechanism으로 automatic speech recognition, speech synthesis, speech repr 등 다양한 문제를 푼 사례가 있음.
- Vision의 방법론을 Audio에 쓴 사례는 그렇게 많지 않음.
- Transformer in Audio Task
- (논문명, 31, 32) : CNN 위에 stacked transformer를 얹음
- (논문명, 33) : 각 transformer module을 CNN과 각각 연결
- 우리는 CNN 없이 multi head attention modules만을 썼다.
- Self-Attention in Audio Task
- (Miyazaki, 34) : BERT에 transformer encoder를 써서 sound event detection을 함. local, global contextual info를 모두 얻을 수 있었음.
- (Koizumi et al, 35) : speech enhancement task를 위한 multi task learning setting에 비슷한 multi-head self attention module을 사용함.
- 우리는 34, 35처럼 있는 구조에 attention module을 더한 게 아니라
III. Method
| Data representation
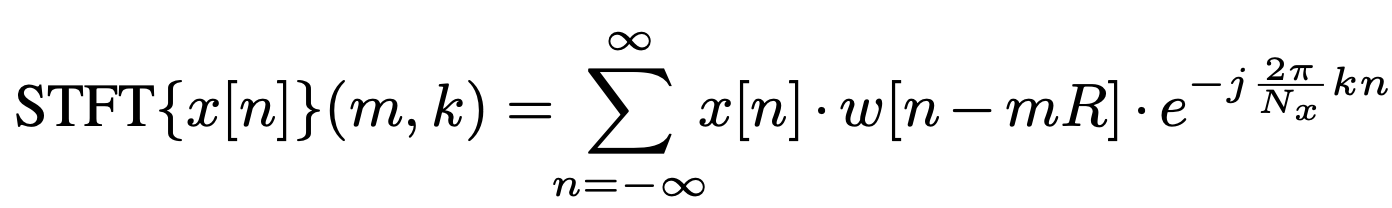
- audio sample을 2D time-frequency Matrix로 변환하여 image-like representation을 얻음
- x[n] : discrete input signal, w[n] : window function, R: hop size
- STFT의 squared magnitude로서 spectrogram을 계산하고, frequency bins을 Mel scale로 mapping한다.
| Overview of out Architecture
- 1st block에 특정 axis(time or freq)를 강요하진 않음.
- 전체 separable transformer block은 L번 반복하여 깊이를 늘릴 수 있음
| Tokenization and linear projection
- spectrogram의 frequency bin이 kp, timeslot이 np라고 하자. 이를 pxp크기의 patch kn개로 나눈다.
- 각 patch를 linear projection block을 통과시켜 d차원 vector로 만든다. 전체 vector set은 R^(n x k x d) 차원이다.
| Vertical Transformer
- 전체 vector T in R^(n x k x d)를 ㅆ
