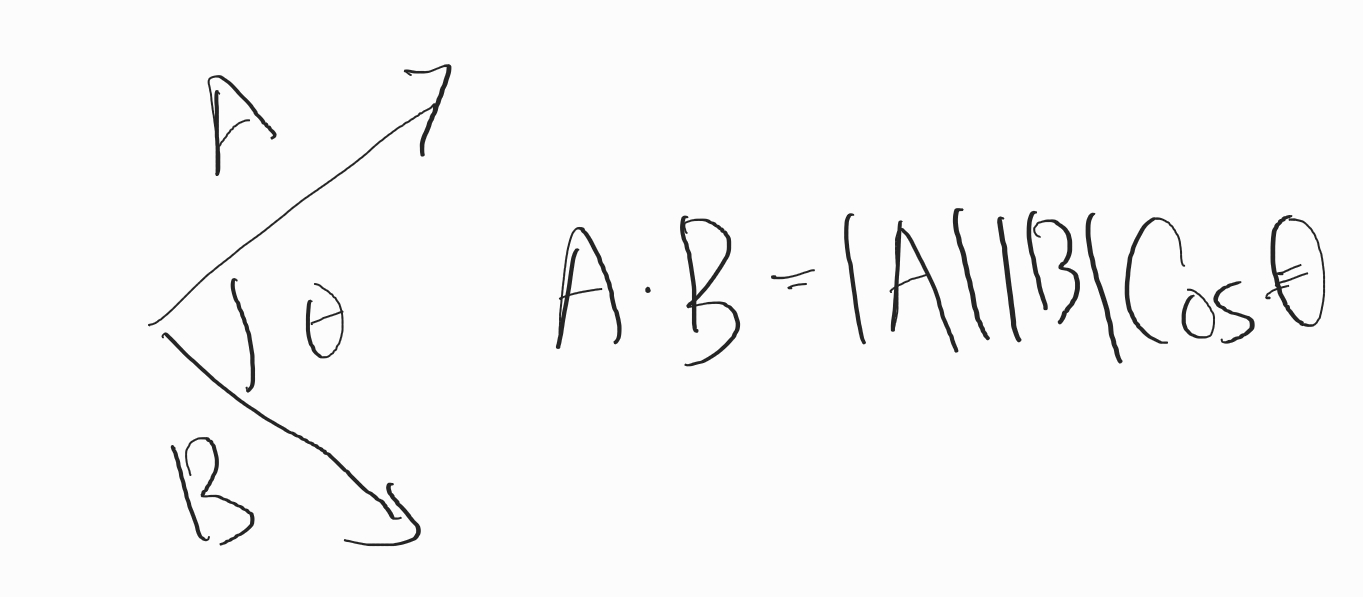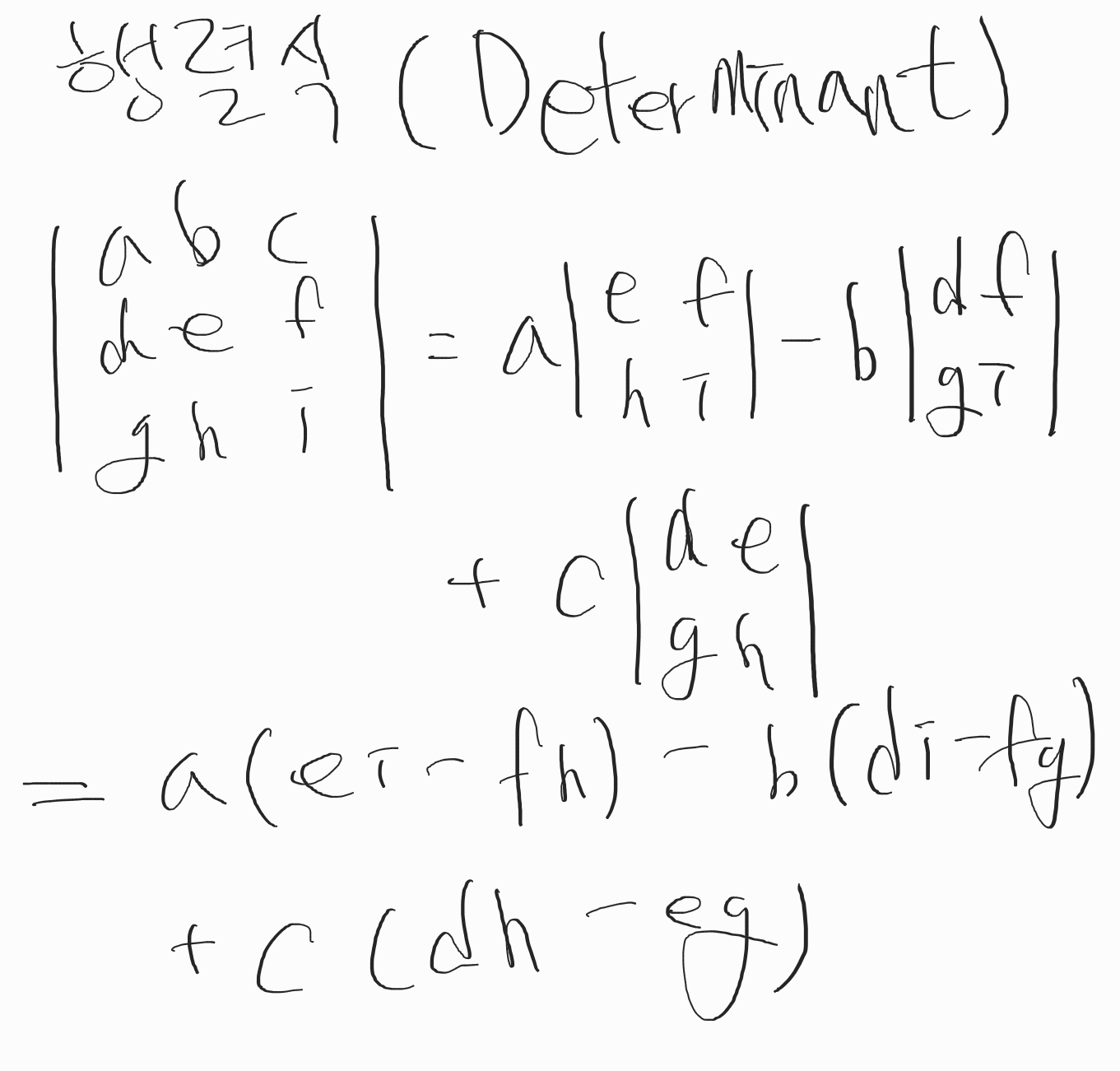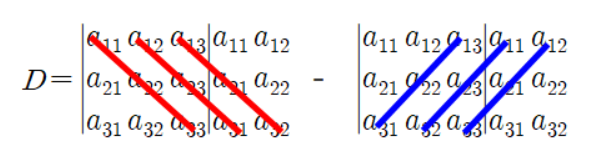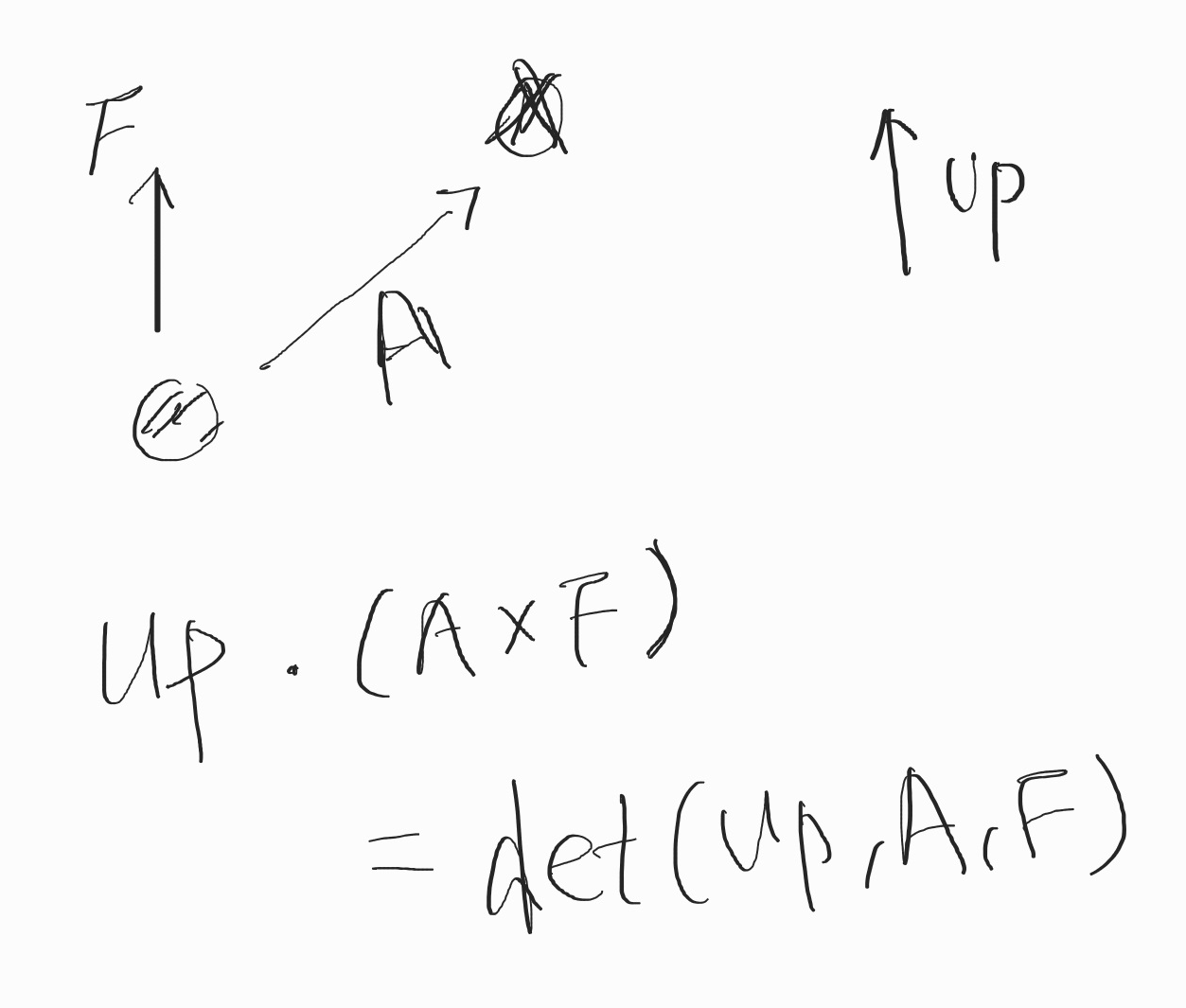게임 프로그래밍에서 왜 벡터를 쓰는가?

게임 프로그래밍에서 왜 벡터를 쓰는가?

• 게임상의 오브젝트들의 정보를 나타낼 때, 좀 더 간단하고 편하게 나타내기 위해서 사용.
• 벡터로 속도, 바람, 저항, 충돌, 위치 판단 등 많은 것들을 표현할 수 있다.

벡터의 내적

정의

• 
• A, B 벡터의 내적은 A벡터와 B벡터의 크기를 각각 곱한 다음 사이각의 Cos값을 곱한 스칼라 값이다.

내적의 특성

• 자기 자신과 내적하면 제곱이다.
  Cos값이 1이므로 같은 벡터 2개를 내적하면 제곱이 된다.
• 두 단위 벡터가 평행하면 절대값 1이다.
  벡터가 평행한 경우는 같은 방향이거나, 반대방향으로 향하는 것이다. 따라서 Cos값이 -1 or 1이 되므로 절대값을 취하면 1이다.

내적을 이용하는 예

두 벡터의 사이각

• 
• 두 벡터의 사이각은 내적공식을 통하여 구할 수 있다.

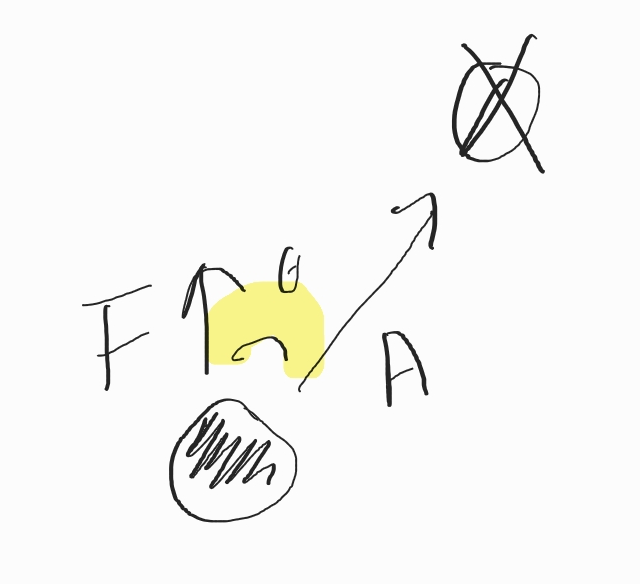
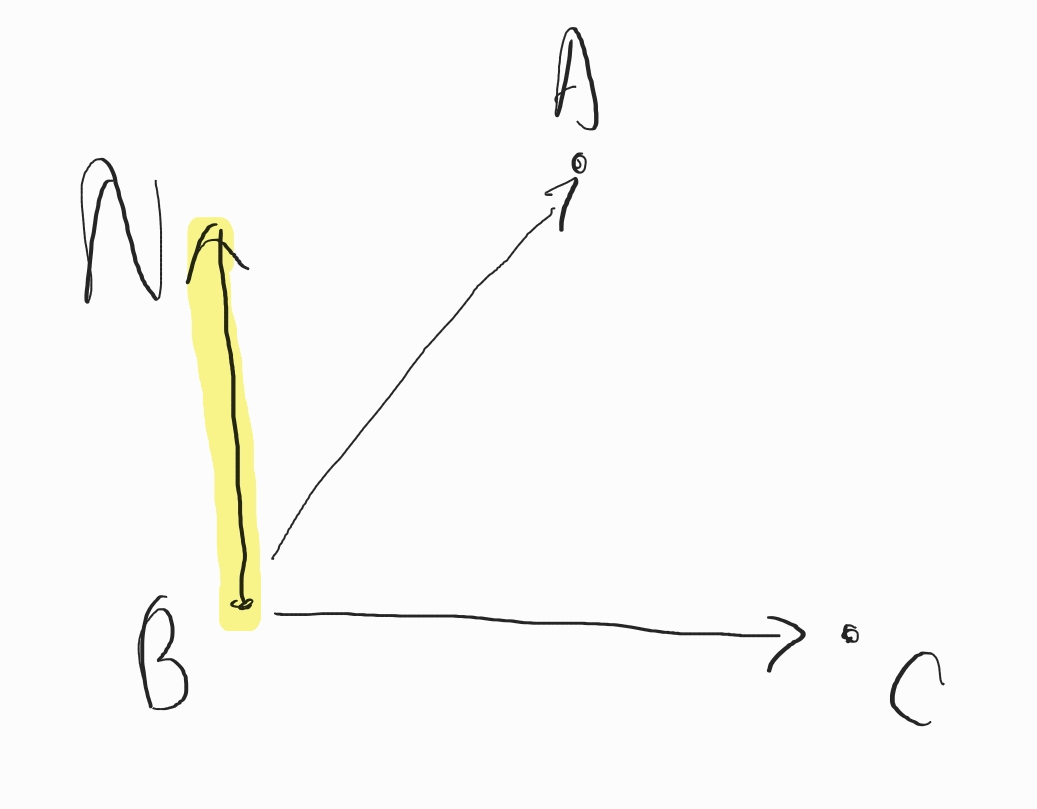
오브젝트와 오브젝트의 관계

• 
• 색칠된 오브젝트를 a, X표시된 오브젝트를 b라고 하겠다.
• a와 b사이의 거리 차이로 나오는 벡터 A와 a의 Forward벡터 간에 내적을 한다.
• 내적한 결과 값중 각도의 값이 -90 ~ 90도 사이에 있으면(즉, cos값이 0보다 크면) a의 전방에 b가 존재하고, 아니면 a의 뒤에 b가 존재하는 것이다.

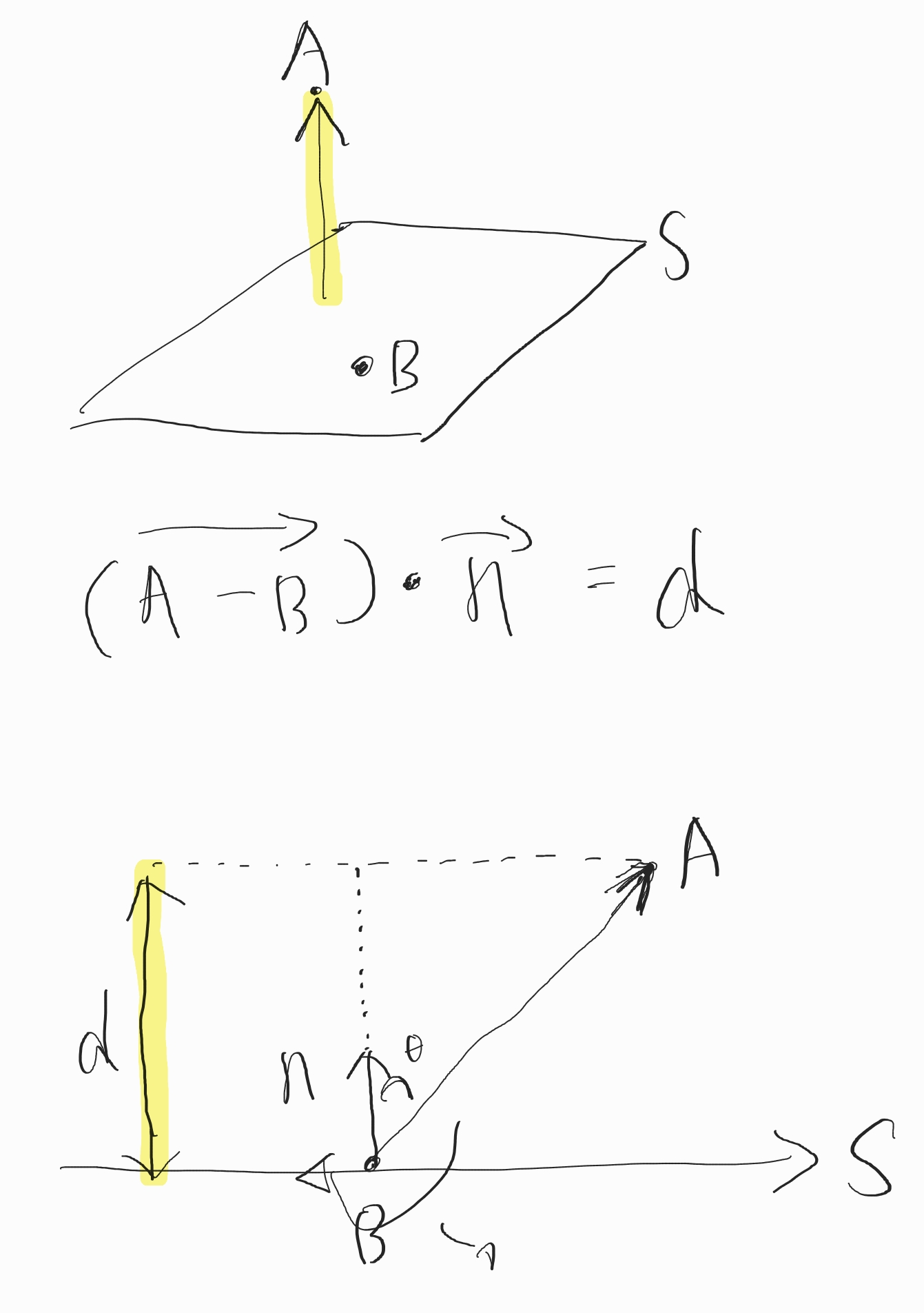
평면과 점 사이의 최단 거리

• 
• 점 A와 평면 S와의 최단거리는 점A와 평면상의 점 B의 방향 벡터와 평면의 단위벡터와의 내적을 통하여 구할 수 있다.

벡터의 외적

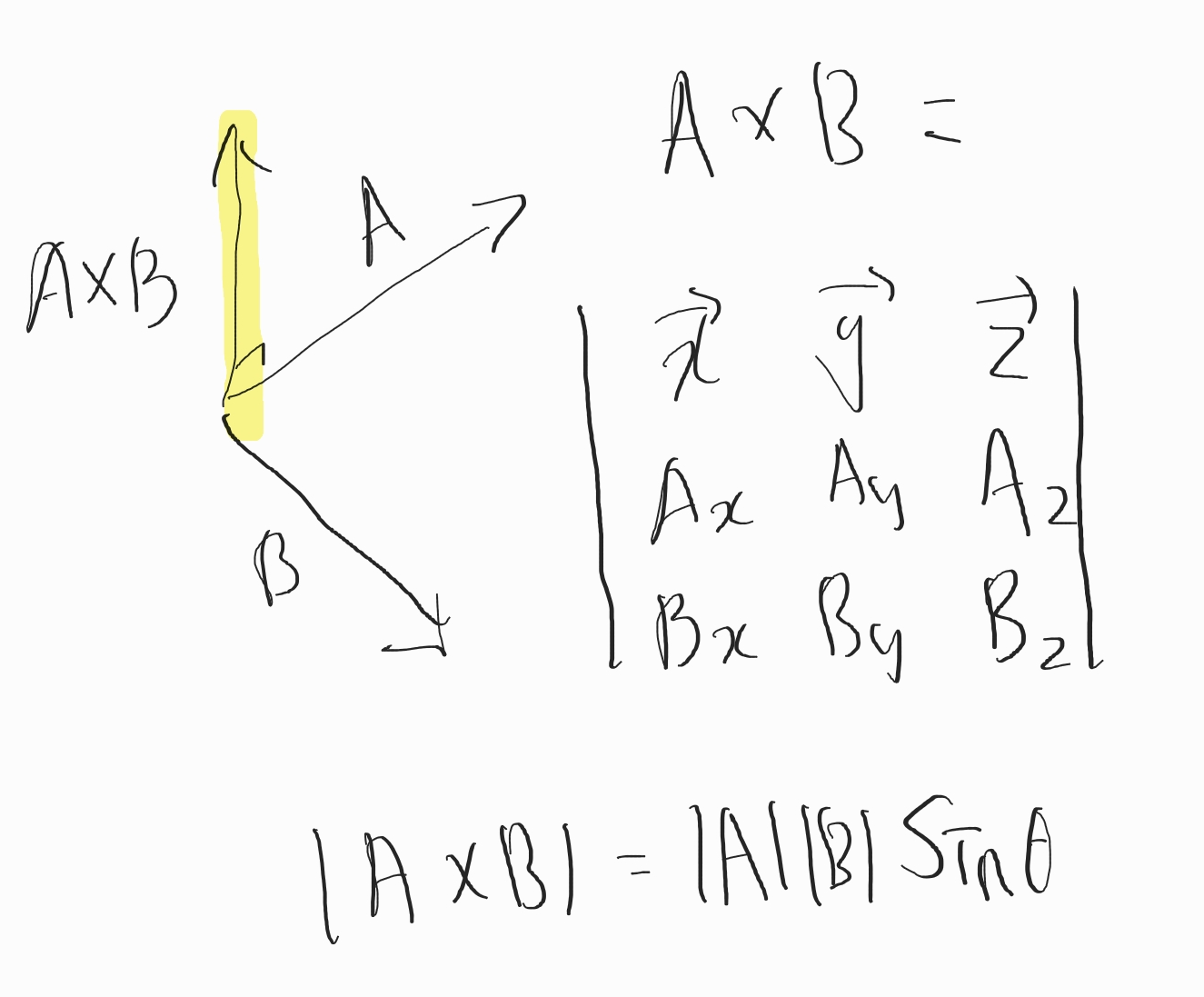
외적의 정의

• 
• 벡터의 외적의 결과는 내적과 달리 또 다른 벡터이다.
• 외적은 위 그림과 같이 행렬식(Determinant)으로 계산 할 수 있다.
• 행렬식의 풀이는 다음과 같다.
• 
• 

외적의 특성

• A와 B의 벡터의 외적, AxB는 A와도 수직이고, B와도 수직이다.
• 내적과 달리 교환 법칙이 성립하지 않으며 순서를 바꾸면 반대 방향의 벡터가 나온다.
  AxB = -(BxA)
• 내적과 동일하게 분배 법칙은 성립한다.
  Ax(B+C) = (AxB) + (AxC)
• 외적 벡터의 크기는 평행사면형의 넓이이다.
• 두 벡터가 평행하면 크기는 0이다.(sin값이 0이기 때문이다.)

외적을 이용하는 예

평면의 법선 벡터를 구할 때 사용

• 
• 삼각형의 세 점을 알고 있을 때. 벡터 2개를 구할 수 있고, 두 벡터의 외적을 구하면 해당 삼각형이 속한 평면의 법선벡터를 구할 수 있다.

한 오브젝트 기준으로 다른 오브젝트가 오른쪽 또는 왼쪽에 있는지 판별

• 
• 월드 좌표계의 UP 방향 벡터를 Up, 색칠된 오브젝트의 Forward벡터를 F, 색칠된 오브젝트와 X표시된 오브젝트 사이의 벡터를 A라 하면, A와 F의 외적 벡터와 Up벡터의 내적을 한 값이 0보다 크면 오른쪽, 0 보다 작으면 왼쪽에 있음을 판별할 수 있다.