오늘 정리할 개념은 점근적 표기와 시간 복잡도이다.
우선 이 개념을 공부하기 이전에 우리가 알아야 하는 것이 있다.

그것은 바로
재귀(자기 호출)이다.

재귀 호출이란?

재귀 호출은 컴퓨터 과학 이론의 근간을 이루는 중요한 개념으로 어떤 문제를 해결하는 과정에서 자신과 똑같지만 크기가 더 작은 문제를 발견하고 이들의 관계를 파악함으로써 문제 해결에 접근하는 방식이다.

보통 재귀를 설명할때는 러시아의 마트료시카를 많이 예시로 든다.

좀 더 직접적인 설명을 보여주기 위해서

팩토리얼을 구하는 간단한 파이썬 코드를 가져왔다.

int factorial(int n){
	if(n <= 1): return 1
    else: return factorial(n - 1)
}

팩토리얼은 n! == n (n - 1) (n - 2) ... 3 2 1 와 같은 공식으로 되어 있는데
이 뜻은 n! == n * (n - 1)! 이라는 의미이기도 하다.
즉 계속해서 재귀호출을 하면 가장 작은 값인 1이 되어 다시 곱해지면서 계속해서 올라간다.

이런 방식으로 큰 문제인 n에서 작은 값인 1로 재귀되어 문제를 해결한다.

알고리즘 역시도 큰 값을 이렇게 재귀를 통해 작은 값으로 성능을 테스트 할 수 있다.

이제 필요한 재귀 개념을 이해했다면

점근적 표기에 대해서도 알아봐요.

점근적 표기

알고리즘은 입력 크기가 작으면 금방 끝나기 때문에 알고리즘의 효율성이 문제가 되는 것은 큰 값의 입력이다.

그렇기 때문에 알고리즘의 성능 테스트를 할 때는 충분히 큰 값에서 이루어지는데 이를 점근적 분석(Asymptotic Analysis)이라 하고 이 때 함수의 입력값에 비례해서 증가하는 것을 점근적 증가율이라고 한다.

하지만 알고리즘의 무조건 큰 값으로만 넣고 그 시간으로 보는 것으로만 알고리즘을 평가하는 것은 좋지 못하다.

왜냐하면 컴퓨터의 성능에따라 생기는 연산속도의 차이가 같은 알고리즘이라도 시간의 차이를 만들 수 있기 때문이다.

그러므로 이런 부분들을 배제하고 성능을 테스트 하기 위해서 사용하는 것이 점근적 표기법이다.

점근적 표기는 성능과 상관없이 알고리즘은 입력 값에 따라 함수의 수행시간이나 사용 공간이 얼마나 되는지 객관적인 기준을 제공해준다.

점근적 표기는 알고리즘의 수행시간을 알기 위해 상세한 부분을 배제하고 중요한 부분만을 집중한다.

점근적 표기에는 몇가지 방법이 있는데 이제 그 방법을 알아 볼 것이다.

Big-O 표기법(빅 오 표기법)

간략하게 말해보자면 상한 표기법이다.

점근적 상한을 알고 있는 경우 사용하는 것으로 '최악의 경우'에도 이 값을 넘지 않는다는 의미이다.
최악의 케이스를 상정으로 두는 표기법이다.

이것을 정의하자면
O(g(n)) = {f(n) | ∃ c > 0, n0 > 0 s.t. ∀ n > n0, f(n) <= cg(n)}
인데 수학적 표현에 대해 무지해서 이 부분이 잘 이해가 안갔었다.
참고로 여기서 '=' 는 '∋' 라는 의미이다.

이 부분을 쉽게 보기 위해 나눠서 해석을 하자면

1. ∃ c > 0, n0 > 0
∃는 Exists란 의미로 존재한다는 뜻이다. 즉 0보다 큰 c와 n0가 존재 한다.

2. s.t. ∀ n > n0, f(n) <= cg(n)
s.t.는 such that으로 아래 조건을 만족한다면 앞에 조건이 만족한다는 의미로 보면 된다.

즉 ∀ n > n0, f(n) <= cg(n)가 성립한다면 ∃ c > 0, n0 > 0이란 뜻이다.

3. ∀ n > n0
∀은 All이라 보면 된다. 모든 n에 대하여란 의미로 s.t.랑 붙어서 생각하면 오른쪽 식이 성립한다는 의미이다.

즉 모든 n0보다 큰 n에 대하여 g(n) <= cf(n)인 0보다 큰 c와 n0가 존재한다는 의미이다.
cf(n)이 f(n)보다 크거나 같은 이유는 Big-O가 상한을 의미하기 대문이다.

그림으로 조금 쉽게 표현하자면

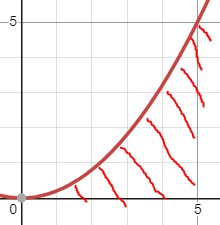
숫자부분은 무시하고 f(n)에 대한 그래프라 했을 때 선을 포함하여 그 보다 작은 부분이 O(f(n))이 된다.

예제를 들어보자면

5n**2 = O(n**2)

위 식이 성립한거를 증명해보자면

5n**2 <= cn ** 2

이 성립하는 c와 n0가 있으면 된다.

이때 n0가 n0 >= 1이라 가정한다면

c가 5 >= c이면 성립하기 때문에 성립하는 c와 n0가 존재한다.

∴5n**2 = O(n**2)

가 성립한다 볼 수 있다.

Big-Ω(빅 오메가 표기법)

빅 오메가 표기법은 빅 오 표기법과 반대되는 개념이라 생각하면 된다. 즉 하한 표기법이다.

점근적 하한을 알고 있는 경우 사용하는 것을 '최적의 경우'를 의미하기도 한다.

이것을 수학적으로 정의하자면
Ω(g(n)) = {f(n) | ∃ c > 0, n0 > 0 s.t. ∀ n > n0, f(n) >= cg(n)}
이 역시도 나눠서 해석해보자면

1. ∃ c > 0, n0 > 0
0보다 큰 c와 n0가 존재한다는 의미이다.

2. s.t. ∀ n > n0, f(n) >= cg(n)
뒤의 조건이 만족하면 앞의 식이 만족된다는 의미이다.

3. ∀ n > n0
모든 n0보다 큰 n에 대하여

즉 모든 n0보다 큰 n에 대하여 f(n) >= cg(n)이 성립한다면 0보다 큰 c, n0가 존재한다는 의미이다.

이 역시도 그림으로 표현하자면

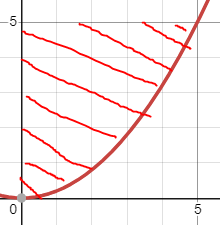
선을 포함하여 그 위가 빅 오메가의 범위이다.

여기도 예제를 보면

5n**2 = Ω(n**2)

이 성립함을 보여라하면

5n**2 >= cn**2

이 성립하기 위해서 n0가 1일 때 5 >= c이면 성립 가능하므로
성립하는 c와 n0가 존재하므로 5n2 = Ω(n2)는 성립한다.

Big-Θ 표기법(빅 세타 표기법)

빅 세타 표기법은 위의 두 표기법의 범위안에 있는 엄밀히 말하자면 그래프의 선부분에 해당된다.

수학적 식으로 표현하면
Θ(g(n)) = O(g(n)) = {f(n) | ∃ c1, c2 > 0, n0 > 0, s.t. ∀ n >= n0, c1g(n) <= f(n) <= c2(g(n))}

위의 두 식들에 비해 복잡해 보이지만 사실 그렇지 않다.

1. ∃ c1, c2 > 0, n0 > 0
0보다 큰 n0와 c1, c2가 존재한다.

2. s.t. ∀ n >= n0, c1g(n) <= f(n) <= c2(g(n))
이 역시도 c1g(n) <= f(n), c2(g(n)) >= f(g(n))이 성립한다면 이란 의미이다.

3. ∀ n >= n0
모든 n0보다 큰 n에 대해서

즉 n0보다 큰 n에 대해서 f(n)보다 작은 c1g(n)과 큰 c2g(n)이 존재한다면 0보다 큰 c1과 c2가 존재한다는 의미이다.

그래프로 표현하면

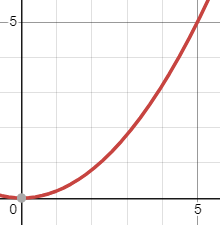
딱 저 선에 해당된다.

이거 역시도 예제를 들어보자면

5n**2 = Θ(n**2)

가 성립함을 보여라하면

그래프상에서 선 부분은 O와 Ω의 교집합 영역이다.

즉 O(n ** 2)와

Ω(n ** 2)가 성립한다면

Θ(n ** 2) 역시도 성립한다.

저 윗부분에서 성립함을 보였으므로 Θ(n ** 2)가 성립한다.