최근 딥러닝 기초를 "혁펜하임의 AI Deep Dive" 강의를 들으며 공부하는 와중에 딥러닝에 대한 통찰을 하게 된 설명에 대해 공유하고자 포스팅을 남긴다.
딥러닝이 무엇일까?
대부분 막연하게 알고 있을 것이다. 경사 하강법...오차역전파...loss 함수...
나도 어떤 학습에는 어떤 loss를 쓰고 그런 것은 알고 있었지만, "왜" 이것을 사용해야 하는지는 정확히 알지 못하였다.
이 부분을 완벽히 이해해보자.
MLE 란?
우선 MLE를 살펴보자.
MLE는 최대 우도법이라고 한다. 사실 와닿지는 않는다.
우도란, 영어로 Likelihood이며 특정 매개변수 하에서 관측된 데이터가 발생할 확률입니다. 즉 특정 데이터를 가장 잘 설명하는 확률 모델의 매개변수를 찾는 것이 MLE라고 할 수 있습니다.
MLE를 구하려면 각 데이터가 나올 확률에 대해 곱해야 합니다. (독립사건이므로)
그러나, 모든 확률은 0~1 사이이므로 그 값들을 곱하면 매우 작은 숫자, underflow 문제가 발생할 수 있습니다.
따라서 log를 씌워서 log-likelihood를 통해 계산합니다.
log를 씌워도 되는 이유는 log 함수는 monotonic increase하기 때문에 log-likelihood를 최대화하는 것이 likelihood를 최대화하는 것과 동일하기 때문입니다.
왜 딥러닝이 MLE일까?
혁펜하임님은 linear regression, binary classification, multi classification을 다르게 생각할 것이 아니라, 그저 예상하는 분포의 차이라고 말씀하셨습니다.
이에 대해 다시 한번 정리해보도록 하겠습니다.
Linear regression
- Linear regression은 가우시안 분포의 평균이 likelihood라고 "가정"해보는 것입니다.
- 이 likelihood를 최대화하는 것이 목표일 것입니다.
- -log를 붙여서 loss 함수로써 사용하는 것입니다!!
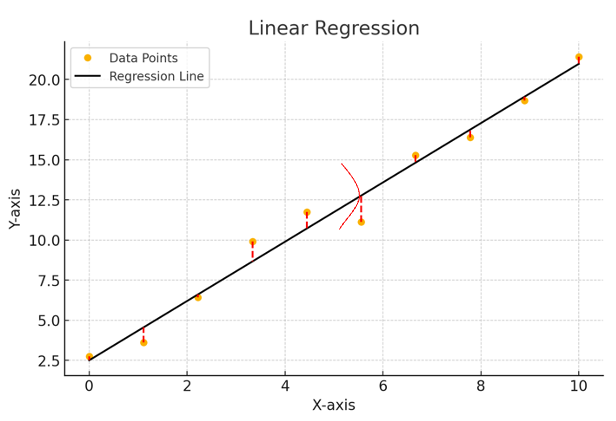
(그림이 이상한 점 이해 부탁드립니다..)
- 수학식으로 표현하자면 다음과 같습니다.
여기에 -log를 취해주면,
다음과 같이 된다.
즉, linear regression 에서는 MSE라는 loss 함수가 자연스레 도출됩니다.
Binary classification
-
이진 분류는 binomial 분포를 likelihood라고 "가정"해보는 것입니다.
-
결국은 0이거나 1인 것이기 때문에 동전 뒤집기라고 생각하면 쉽게 이해가 가능할 것입니다.
-
수학 식으로 표현하면 다음과 같다
해당 식에 -log를 취해주면, -ylogq 들의 합으로 표현될 수 있고, 이것을 minimum 하는 것이 원래의 식을 maximum 하는 것과 같다. 이 식이 BCE, Binary Cross Entropy 라고 볼 수 있다.
Multi Classification
- 다중 분류는 multinomial 분포를 likelihood라고 "가정"해보는 것입니다.
- 만약 개, 고양이, 소 3개의 동물을 분류한다고 가정해봅시다.
- 그렇다면 loss는 다음과 같습니다.
- 여기에 -log를 취하면,
다음과 같습니다.
one-hot encoding으로 분류를 진행할 때, 만약 y1이 개라면, 예상 값 [q1,q2,q3]에 대해 개를 정확히 예측하여 [1,0,0]라고 했다면, loss는 0일 것이다. 고양이와 소에도 마찬가지로 loss는 0일 것이다.
즉, loss는 0보다 크거나 같은 값이다.
해당 loss가 바로 cross-entropy이다.
이렇게, 딥러닝에서 weight를 업데이트하기 위한 loss들이 갑자기 툭 튀어나온 것이 아니라, 분포를 가정하여 나온 것을 확인할 수 있습니다. 결국 딥러닝이란 이러한 가능도(likelihood)를 최대화하는 것이 목표이다.
- 세그멘테이션 연구를 진행할 때 사용한 Dice loss는 평가 지표은 Dice Score를 loss로 활용한 것이기 때문에 어떠한 분포를 가정할 수는 없다고 생각한다.
*해당 내용은 혁펜하임 AI Deep dive 수업을 정리하고 저의 느낀 점을 작성한 것입니다.





