이번 게시물에서는 파이썬 코드로 직접 MSE를 계산하고 경사하강법을 적용하여
보스턴 주택 가격을 예측해보는 코드를 리뷰해보겠습니다!
모든 이미지 출처 : 인프런 딥러닝 CNN 완벽 가이드 - Fundamental 편
MSE 직접 계산하여 경사 하강법에 적용
from sklearn.datasets import load_boston
boston = load_boston()
bostonDF = pd.DataFrame(boston.data, columns=boston.feature_names)
bostonDF['PRICE'] = boston.target # dataframe에 PRICE 추가
print(bostonDF.shape) # row, column
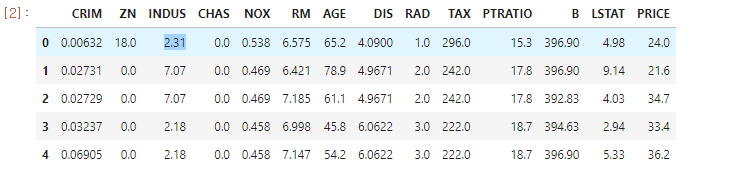
bostonDF.head() #앞의 5개만 가져오기- 처음으로는 보스턴 주택 데이터를 가져오기 위해
sklearn의load_boston을 사용합니다. - 가져온
load_boston을 데이터 프레임으로 만들어주고, 각 열은boston.feature_names로 만들어줍니다.
(1) 가중치 업데이트 함수 만들기 !

- 위와 같이 bias와 가중치 값을 업데이트할 수 있습니다.
(가중치에 대해 편미분하여이전 가중치에편미분한 값 * 학습률을 빼서 업데이트합니다!)
def get_update_weights_value(bias,w1,w2,rm,lstat,target,learning_rate) :
# 데이터 건수
N = len(target)
# 예측값
predicted = bias + w1*rm + w2 *lstat
# 차이값
diff = target - predicted
bias_factors = np.ones((N,)) #N 행만큼 1로 만들어줌 (bias 업데이트를 위해)
#얼마나 update할 지 정하기
w1_update = -(2/N)*learning_rate*(np.dot(rm.T, diff))
w2_update = -(2/N)*learning_rate*(np.dot(lstat.T,diff))
bias_update = -(2/N)*learning_rate*(np.dot(bias_factors.T,diff))
#예측값 MSE 구하기
mse_loss = np.mean(np.square(diff))
return bias_update, w1_update, w2_update, mse_loss
(2) 경사 하강법 함수 만들기 !
# RM, LSTAT feature array와 PRICE target array를 입력 받아서 iter_epochs수만큼 반복적으로 Weight와 Bias를 update적용.
def gradient_descent(features, target, iter_epochs=1000, verbose=True):
w1 = np.zeros((1,))
w2 = np.zeros((1,))
bias = np.zeros((1,))
print('최초 w1, w2, bias : ',w1,w2,bias) #최초 w1,w2,bias 출력
learning_rate = 0.01
rm = features[:, 0]
lstat = features[:, 1]
for i in range(iter_epochs):
bias_update, w1_update, w2_update, loss = get_update_weights_value(bias, w1, w2, rm, lstat, target, learning_rate)
w1 = w1 - w1_update #w1 업데이트
w2 = w2 - w2_update #w2 업데이트
bias = bias - bias_update
#if verbose:
#print('Epoch:', i+1,'/', iter_epochs)
#print('w1:', w1, 'w2:', w2, 'bias:', bias, 'loss:', loss)
return w1, w2, bias
(3) 적용해보기
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler() # 0~1 사이로 정규화
scaled_features = scaler.fit_transform(bostonDF[['RM', 'LSTAT']]) # fit_transform 안에 쓴 df를 0~1로 정규화해줌
w1, w2, bias = gradient_descent(scaled_features, bostonDF['PRICE'].values, iter_epochs=5000, verbose=True)
print('##### 최종 w1, w2, bias #######')
print(w1, w2, bias)- 보스턴 주택의 특징인 'RM', 'LSTAT'이 0~1 사이 값을 갖도록
MinMaxScaler를 통해
정규화 시켜줍니다. - 그 후 w1, w2, bias 최종 업데이트 값을 저장합니다.
(4) 결과 확인
predicted = scaled_features[:, 0]*w1 + scaled_features[:, 1]*w2 + bias
bostonDF['PREDICTED_PRICE'] = predicted
bostonDF.head(10)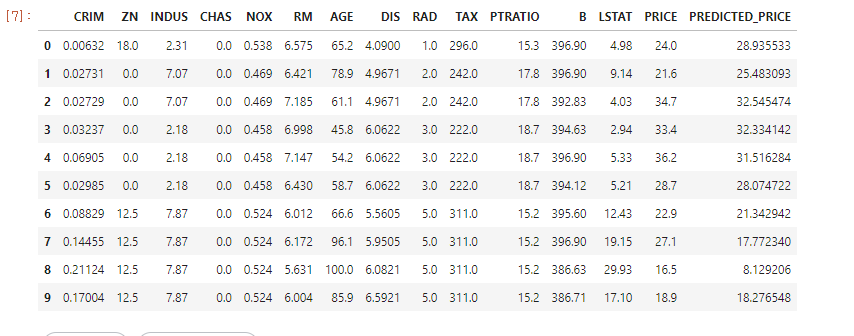
PREDICTED_PRICE: 최종 예측값
실제로 MSE를 계산하여 경사하강법을 적용해보았습니다!
MSE는 오차의 제곱을 구하는 것이어서, 실제 Price와의 오차가 많이 날 수 있는 단점이 있다는 것을 알았네요...!
