[LeetCode] Unique Binary Search Trees II ( 반드시 다시 풀어보기 )

이진트리 개념을 알고 있어도 빠르게 적용을 자꾸 못하는 것 같아서 이번에도 이진탐색 트리 문제를 풀어보기로 했다.

역시 부족하다는 것을 많이 느꼈다

Unique Binary Search Trees II - LeetCode

n이 주어졌을 때 1~n 까지 유니크한 값들로 이루어진 노드들로 만들 수 있는 BST의 모든 경우를 리턴하라.

풀이과정 ( 잘못된 풀이 )

( 딱 봐도 경우의 수가 많을 것 같은데 n이 1이상 8 이하로 제한되어있다. )

BST ( Binary Search Tree ) 는 어떤 규칙이 정해져 있다.

어떤 노드의 left subtree는 그 노드보다 작은 값들로 이루어져 있다.

어떤 노드의 right subtree는 그 노드보다 큰 값들로 이루어져 있다.

이 문제는 각 정답 트리들을, root인 TreeNode를 전달함으로서 완성해야한다.

• 이를 위해서는 deepcopy를 해야 하고
• delete 또한 할 수 있어야 한다.

root에 대해서는 각 경우를 미리 해 보고

for(int i=1; i <=n ;i++){
	root = new TreeNode(i);
	visit[i] = true; 
	recur(2);
	visit[i] = false; 
}

재귀적으로 , 하나의 숫자씩 각 위치를 찾아나가기

n개를 가진 tree가 완성되면, 이 tree를 deecopy하여, 새로운 트리를 생성하여 이를 answer로 덧붙이기

backtrack시, 기존에 붙인 노드를 null로 처리하기

	
public void recur(int cnt){
	if( cnt > sn ) {
		// deepcopy
		ans.add(deepcopy(root);
		return; 
	} 
	for(int i=1; i <=n ;i++ ){
		if(visit[i] == true ) continue;
		visit[i] = true; 
		TreeNode par = findLoc(i,root);
		recur(cnt+1);
		// delete code 
		if( par.val > i ) par.left = null;
		else par.right = null;
		visit[i] = false; 
	}
}

 
public TreeNode deepcopy(TreeNode cur){
	TreeNode cop = new TreeNode(cur.val);
	if(cur.left != null){
		cop.left = deepcopy( cur.left );
	}
	if(cur.right != null){
		cop.right = deepcopy(cur.right);
	}
	return cop; 
}

// Location을 찾는 코드 
// target을 child로 붙이는 parent 노드를 리턴한다. 
TreeNode findLoc(int target, TreeNode par){
	while(true){
		if(par.val < target){
			if(par.right != null){
				return findLoc(target,par.right);
			}else{
				return par; 
			}
		}else{
			if(par.left != null){
				return findLoc(target, par.left);
			}else{
				return par;
			}
		}
}

위의 풀이과정 문제점 : 중복된 답 도출

• 매번 1 ~ n 까지의 숫자를 붙여나가는데, BST 이다 보니, 동일한 Tree가 나오는 경우가 생기게 된다.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
import java.util.*;
class Solution {
    public List<TreeNode> ans = new LinkedList<>();
    public boolean[] visit;
    public int sn;
    public TreeNode root; 
    
    
    public List<TreeNode> generateTrees(int n) {
        visit = new boolean[n+1]; // 1 ~ n integer
        sn = n; 

        for(int i=1; i <=n ;i++){
	        root = new TreeNode(i);
	        visit[i] = true; 
	        recur(2);
	        visit[i] = false; 
        }
        
        
        return ans;
    }
    public void recur(int cnt){
	    if( cnt > sn ) {
	    	// deepcopy
	    	ans.add(deepcopy(root));
	    	return; 
        }
	    for(int i=1; i <=sn ;i++ ){
		    if(visit[i] == true ) continue;
            visit[i]=true;
		    TreeNode par = findLoc(i,root);
		    recur(cnt+1);
		    // delete code 
		    if( par.val > i ) par.left = null;
		    else par.right = null;
		    visit[i] = false; 
	     }
    }
    // Location을 찾는 코드 
    TreeNode findLoc(int target, TreeNode par){
        
	    while(true){
		    if(par.val < target){
			    if(par.right != null){
			    	return findLoc(target,par.right);
			    }else{
                    par.right = new TreeNode(target);
				    return par; 
			    }
		    }else{
			    if(par.left != null){
				    return findLoc(target, par.left);
			    }else{
                    par.left = new TreeNode(target);
				    return par;
			    }
		    }
        }
    }
    public TreeNode deepcopy(TreeNode cur){
	    TreeNode cop = new TreeNode(cur.val);
	    if(cur.left != null){
		    cop.left = deepcopy( cur.left );
	    }
	    if(cur.right != null){
		    cop.right = deepcopy(cur.right);
	    }
	    return cop; 
    }
}

다른사람의 풀이 : 재귀적 풀이

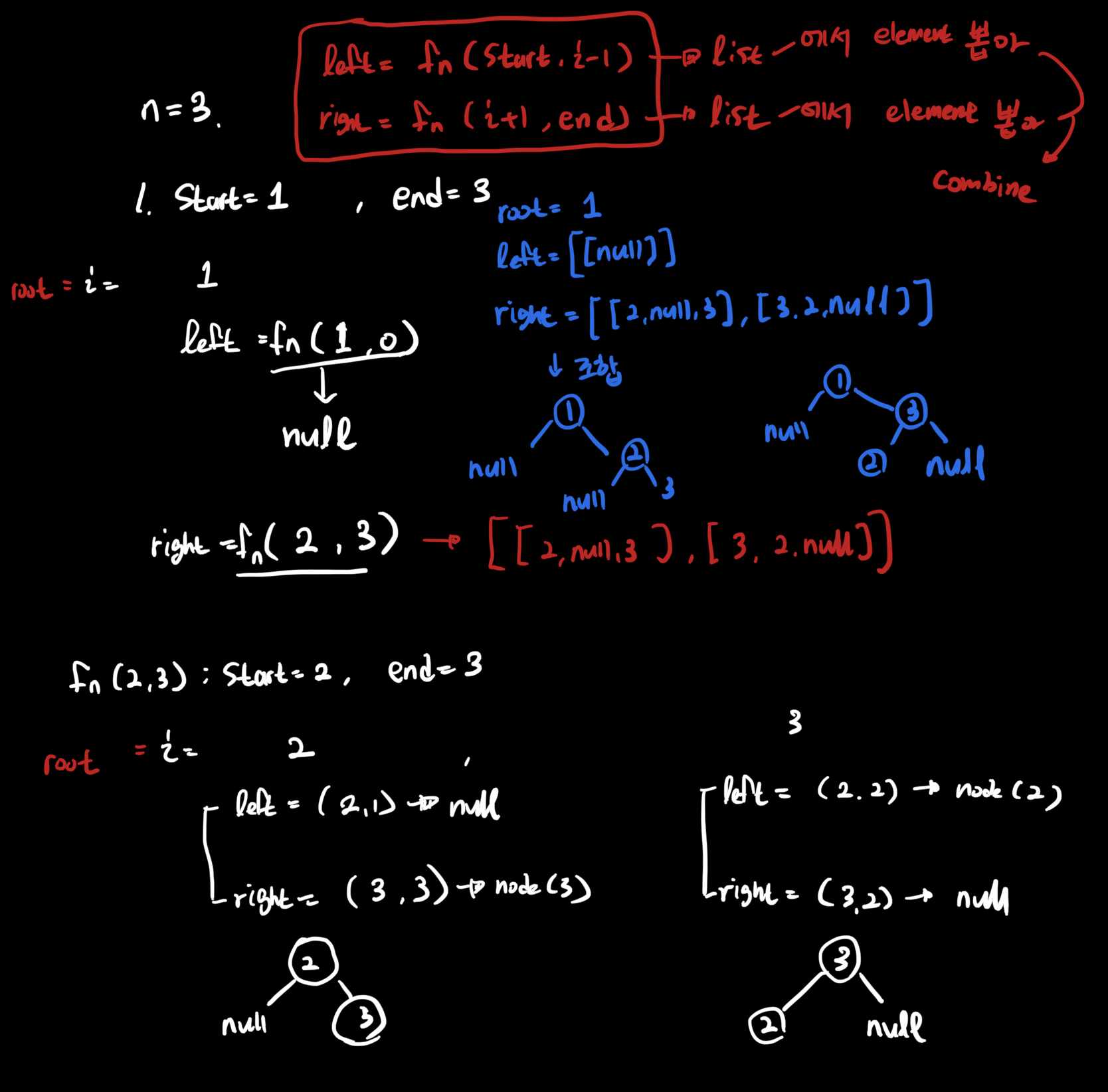
• 일단 정답의 형태는 , 1~n으로 생성되는 BST를 in-order traverse를 한 형태임을 볼 수 있다.
• 따라서 i번째 노드를 root로 선택하게 된다면, left subtree는 1 ~ ( i -1 ) 까지의 원소들을 담을 것이고, right subtree는 ( i + 1 ) ~ n 까지의 원소들을 담을 것이다.
• 따라서 재귀호출을 사용하여, 모든 가능한 left, right subtree들을 생성한 후, root 와 combine하는 방식을 사용할 수 있다.

일종의, divide and conquer로 문제를 푸는 것 같았다.

• 재귀적으로 호출되는 함수에서는 , 정수 start ~ end 를 사용하여 생성 가능한 모든 Tree의 list를 리턴하도록 한다.
  • leaf node인 경우
    • start == end → 값을 contain하는 leaf node
    • start < end → null인 leaf node
  • 리턴되어오는 left, right 각각의 [ 생성 가능한 모든 Tree의 list ] 들로부터, root의 서브트리 조합을 생성할 수 있다.
  • 매 번 root를 생성하는 것에 주의한다 . ( 그렇지 않으면, 기존의 것을 대체하게 되어버린다 )

재귀 호출하는 함수에서는, 현재 노드의 left subtree 또는 right subtree를 생성하여 리턴한다.
아래 그림은, n이 3일 때, 그리고 가장 최상위 root node가 1일 때만을 나타내 보았다.

public List<TreeNode> generateTrees(int n){
	return genTrees(1,n);
}
public List<TreeNode> genTrees(int start, int end){
	List<TreeNode> list = new ArrayList<TreeNode>();
	
	if( start > end ){
		list.add(null);
		return list; 
	} 
	if( start == end ){
		list.add( new TreeNode(start));
		return list; 
	} 
	
	List<TreeNode> left,right;
	
	for(int i = start ; i<= end; i++){
		// left subtree로 올 수 있는 가능한 조합들이 리턴됨
		left = genTrees(start, i-1);
		// right subtree로 올 수 있는 가능한 조합들이 리턴됨 
		right = genTrees(i+1, end);
		// root가 i 일 때 , 가능한 left, right 서브트리 경우들로부터
		// left, right 서브트리 조합을 생성한다. 
		for(TreeNode lnode : left ){
			for(TreeNode rnode : right ){
				TreeNode root = new TreeNode(i);
				root.left = lnode; 
				root.right = rnode;
				list.add(root);
			}
		}
	}
	return list; 
}