[LeetCode]3Sum ( 다시 풀어볼 것 )

• 조합으로 푼다면? → 3000C3 → 4495501000 .. 이건 절대 안된다

i ≠ j ≠k 일 때, 실제 값의 합은 0 이어야 한다.

투 포인터의 연장선처럼 풀 수 있지 않을까???

따라서 a,b,c 라는 포인터를 두고, a를 하나 결정하고, b c 는 투포인터로 사용하는 방식을 떠올렸다.

• index 0 에서부터 시작하여 a를 설정하고, 그 오른쪽 부분에서 투포인터를 돌린다 -> O(n^2)
  

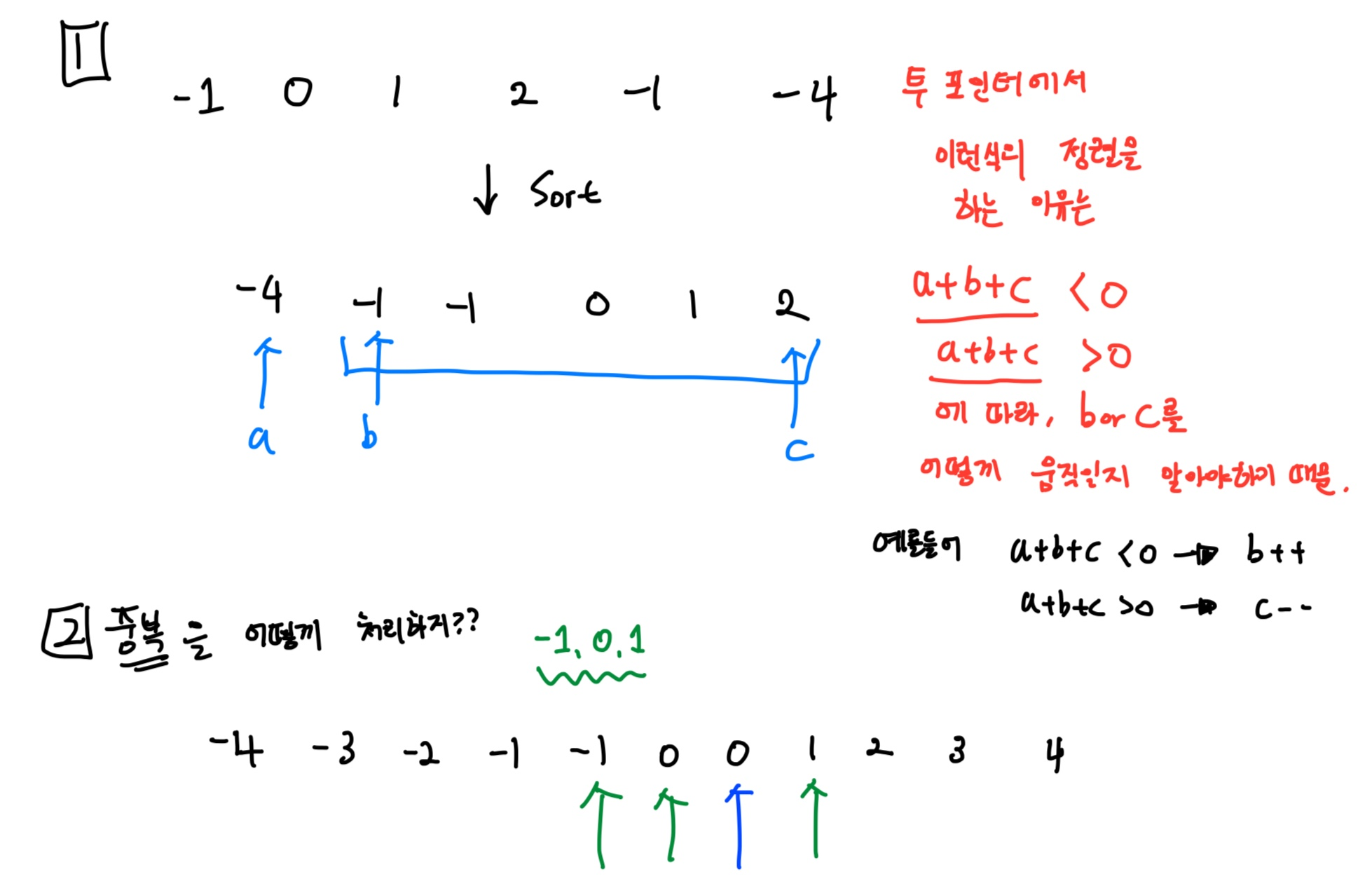
• 이 문제에서 주의할 것은 “duplicated 즉, 중복된 경우” 가 없어야 한다는 것이다.

문제 풀이 ( 풀지 못했다 )

중복을 없애는 것이 관건이었다.

실제로 다른 사람의 코드를 보고 정말 신기했던 부분이다.

for a in range(len(nums)-2):
	if a > 0 and nums[a] == nums[a-1]:
		continue

1. a 를 선택하고 , b,c를 선택해야하기 때문에 nums의 길이 -2 인 range 여야 한다.

   • range(x) 는 0 ~ x -1 인 int list를 반환하기 때문임.

2. if a > 0 and nums[a] == nums[a-1]:

   • 일단 nums[a] == nums[a-1] 이면 지나간다 → 이는, 중복된 a에 대해 수행하지 않기 위함이다.
   • 그렇다면 a > 0 은 왜 오는가?
     • a가 0인 경우에는, 첫 번째로 나오는 것이라, 비교할 이전 게 없음.

   따라서 a >0 이고 nums[a ] == nums[a-1]이면 중복된 경우들을 만들어 내니 pass한다.

그 다음에 중복이 일어날 수 있는 상황은 뭐가 있을까?

• b 랑 c 로 인한 중복이다.
• 특히나 b 또는 c 중 하나라도 중복된다면 무조건 b,c는 같이 중복되는 경우일 수 밖에 없다. ( a+ b+ c = 0 이어야 하기 때문에 , 항상 a = -b-c 로 -b-c는 항상 어떤 상수 값과 같아야하기 때문 )
  • 따라서, 어떤 a에 대해, b,c 는, 다음에 이동했을 때의 b,c와 같지 않을 때 까지 움직여야 한다.

def threeSum(self, nums: List[int]) -> List[List[int]]:
        ans = []
        nums.sort()
        for a in range(len(nums)-2):
            # 중복된 a 인 경우 는 pass 한다  
            # 단, a가 0 일 때는 이전 값이 없기 때문에 제외시켜야함 (0-1)은 Out of Range가 되니까
            if a > 0 and nums[a] == nums[a-1]:
                continue
            # b,c라는 투포인터를 사용한다. 이 때 중복되는 b,c를 제외시켜야한다
            b = a + 1
            c = len(nums) - 1
            while b < c:
                # 먼저, nums[a] + nums[b] + nums[c] 가 0 보다 크다면 오른쪽(더 큰 값) 을 감소시켜줘야한다
                if nums[a] + nums[b] + nums[c] > 0:
                    c -= 1
                # nums[a] + nums[b] + nums[c] 가 0 보다 작다면, 작은 값 을 크게 해 줘야 한다
                elif nums[a] + nums[b] + nums[c] < 0:
                    b += 1
                else:
                    # 정답 리스트에 추가한다
                    ans.append([nums[a] , nums[b] ,nums[c]])
                    # 이 때 이렇게 나온 b 또는 c는 여러개가 존재할 수도 있다. 
                    # 이들을 건너 뛰어서 중복되지 않는 b,c로 update 시켜줘 놓아야  중복되는 경우가 생기지 않는다.
                    while b < c and nums[b] == nums[b+1]:
                        b += 1
                    b += 1
                    while b < c and nums[c] == nums[c-1]:
                        c -= 1
                    c -= 1
        return ans