[백준] 2352번 반도체 설계

2352번: 반도체 설계

문제 해결

전깃줄 문제가 생각나는데, 문제 유형이 뭐였는지도 기억이 또 안 났다ㅋㅋ;

일단 이 문제를 읽고 생각 해 보면, 최장 증가 수열이 생각난다.

왜냐하면, a 번째 포트에 연결된 a’이 있다고 하자. a 포트 아래의 포트를 b라고 하면 b’은 a’보다 같거나 작아서는 안 되기 때문이다.

생각해보면, 이는 “최장 증가 수열”을 구해야 하는 것과 같다.

index i 부터의 최장증가수열을 구하라고 한다면 →

1. 이전의 수가 arr[i] 보다 작고 && i번째 원소를 포함시킨 최장 증가수열
2. i 번째 수를 첫 번째 수로 하는 최장증가수열
3. i 번째 수를 포함시키지 않는 최장 증가수열

그런데 생각해 보니 → 결국 이를 위해서는, pre를 저장하고 있어야하고, 그러면 [ i][ pre ] 이런식으로 cache[i][pre]를 저장해야하며, 모든 경우의 각 (i,pre) pair에 대해 동적 계획법을 통해 단 한 번씩만 연산을 하게 된다고 하더라도 결국 O(n^2)이다.

위의 방식은 중첩된 이중 for문을 통해서도 나타낼 수 있다

단, 위의 방식은 결국 재귀적 동적 계획법으로 top down인 거고 , 이중 for문을 통하는 것은 bottom up 방식이며 반복적 동적 계획법인것이다.

아무튼 둘 다 O(n^2)이 되어버림.

여기서는 n이 40000이기 때문에 이 방식은 사용불가능하다.

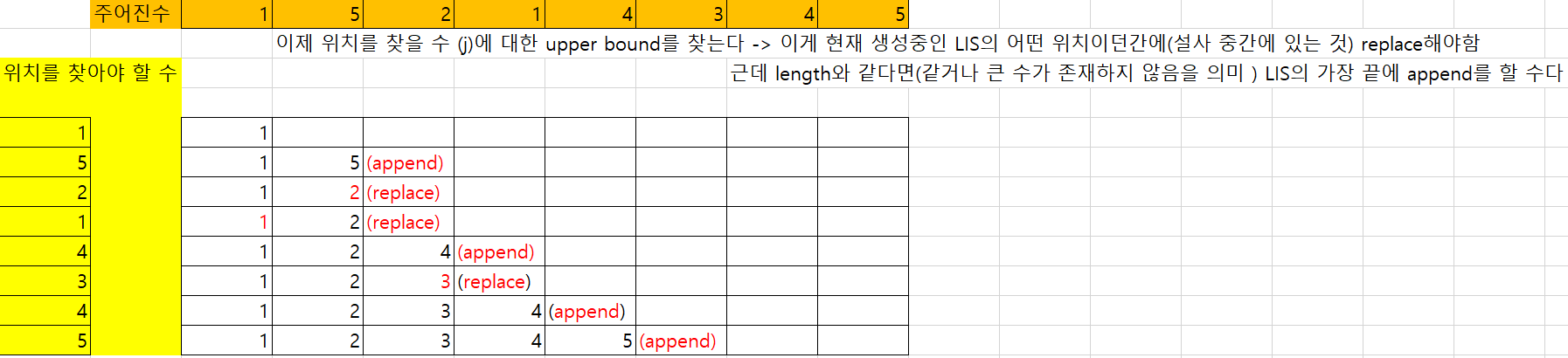
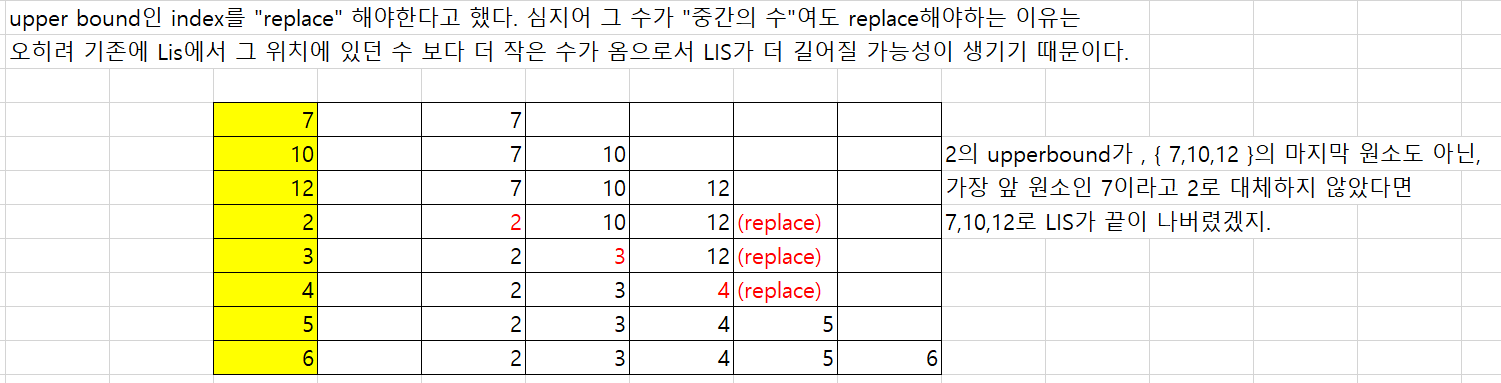
시간복잡도 O(nlogn)을 갖는 방법 : i=0 ~ end 까지의 수에 대해서, 이진탐색을 사용 : LIS를 유지하기 위한 "최적의 위치에다" 수를 삽입

• index 0 부터 시작하여, 다음 수를 LIS라는 비어있는 리스트에 추가해 나가는데
  • 이 때, LIS를 유지하면서, 다음 수를 추가해야함.
  • 따라서, 이분탐색을 이용하여, 다음수 를 추가할 위치를 찾는다 : upper bound를 찾는다

for(int i=0;i<len;i++){
	idx = upper_bound(i); // index i인 애의 upper bound 위치
	if( idx == len ) list.add(arr[i]); // append
	else list.set( idx,arr[i] ); // replace
}

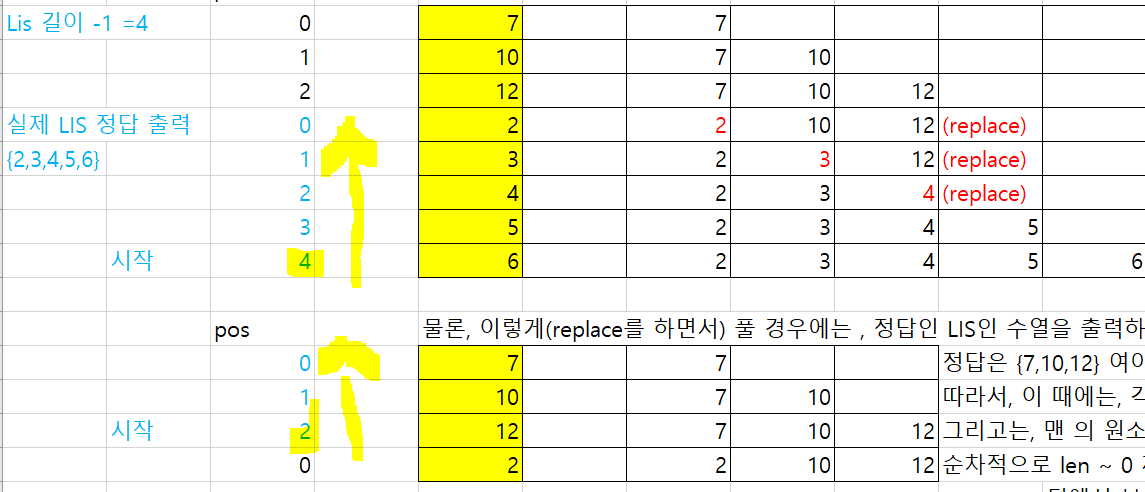
실제 문자열을 구하라는 식의 문제라면

1. pos 위치를 저장하고
2. array의 pos 위치를 저장해 놓은 배열을 돌면서, 실제 LIS를 생성

for(int i=0;i<len;i++){
	idx = upper_bound(i); // index i인 애의 upper bound 위치
	if( idx == len ) {
			list.add(arr[i]); // append
			pos[i] = list.size()-1;
	}
	else {
		list.set( idx, arr[i] ); // replace
		pos[i] = idx; 
	}
}

public static void makeStr(){
		int total = lis.size()-1;
		int p = pos.length -1;
		LinkedList<Integer> ans = new LinkedList<>();
		while( p >= 0){
			if(pos[] == total){
				ans.addFirst(arr[p]);
				total--;
			}
			p--;
		}
		// StringBuilder를 사용해, ans로부터 문자열을 생성하여 출력할 수 있음. 
}