• 삽입과 삭제는 FIFO방식으로 이루어진다 ( First in First Out)
  • 삽입은 rear에서, 삭제는 front에서
• java의 경우 예외처리 두 가지 EmptyQueueException , FullQueueException.

Array based Queue

• size N 의 array를 사용, front, rear변수를 사용해 각각 추적한다.
  • front는 front element의 index. - 즉 , 먼저 push된 element가 들어있다.- 즉, pop 할 장소.
  • rear은 마지막 element의 바로 뒤를 가리킨다. - 즉, push 할 장소이다. 항상 empty element를 가리키고 있다. —> rear에 push한다.
• array는 limited size인데, 이 크기 N의 array를 circular fashion으로 operate한다. Circular array를 구현하는게 좋을 거다.
  • 즉, f 또는 r이 N-1을 초과하면, 0으로 reset시킨다. —> 즉 f % N 값으로 ( r % N 값으로 세팅)
  • full상태와 emtpy상태의 구분?
    • initial 상태 : f = -1, r = 0 . 이라고 해 놓고, push하면 무조건 f++
    • empty 상태 : f = r 일 때 + r이 empty
    • full 상태 : 역시 f = r일 때 + r위치가 full인 경우.
  • circular array를 구현하기 위해서는 modulo % 연산자를 사용해야 한다.
• size구하는 함수 ? N 개에서 비어있는 element 개수를 빼면 된다.
  • Circular한 구현이 되어있는 경우.
    • f < r : r - f —> 이것은 (N - (f-r)) %N과도 같다. .
      • modulo 연산의 특징 : (N%N - (f-r)%N) %N = (r-f)%N = r-f
    • r < f : N - ( f-r)
  • size구하는 함수 최종 : (N - (f-r)) % N ( 따로 size를 count하는 변수를 두지 않고도 괜찮다)

예외처리

• enqueue(o) throw FullQueueException
• dequeue() throw EmptyQueueException

Queue의 Applications

• 직접적으로 사용되는곳
  • Round Robin 스케줄링 (OS)
    • Multi-tasking (CPU time sharing)
    • Packet switching networks(shared physical medium)
    • shared device
  • RR Scheduler에서는, process를 각 queue(run큐, Ready큐, Waiting 큐..)에 넣어놓고 각 queue에서 dequeue해 온 프로세스를 run /ready/wait하게 된다.
• 다른 자료구조나, 알고리즘을 구현하는데 많이 사용

Deque(덱) : Double-Ended queue

• cpp의
• front와 end 양쪽에서 insertion과 removal이 모두 가능.
• dequeue를 구현하기 위해 Array보다는 Node list를 만드는 것이 효과적이다.

JAVA의 Deque operations

Main deque operations

1. addFirst ( object): inserts an element at the front of the deque
2. addLast ( object): inserts an element at the rear of the deque
3. object removeFirst ()(): removes and returns the element at the front of the deque
4. object removeLast ()(): removes and returns the element at the rear of the deque

Auxiliary deque operations

1. object getFirst ()(): returns the element at the front without removing it
2. object getLast ()(): returns the element at the rear without removing it
3. integer size ()(): returns the number of elements stored
4. boolean isEmpty ()(): indicates whether no elements are stored

cpp의 dequeue operation

• push_back /pop_back

• push_front / pop_front

• at() : random access —→ O(1)

• 초기값과 함께 construct 예시

  #include <deque>
  int main()
  {
  	std::deque<int> d = {7,5,16,8};
  	//Add elements
  	d.push_front(13);
  	d.push_back(25);
  	// Iterate and print values of deque
  	for(int n : d){
  		std::cout<<n<<'\n';
  	}
  }

• front, back에서 매우 빠른 insertion과 deletion이 가능하다 :

• std::vector와 다르게, deque의 elements는 contiguosly하게 stored되지 않는다.

  • 구현되어 있는 방식 : a sequence of individually allocated fixed-size arrays, with additional bookkeeping.
  • 즉, deque에 대한 indexed access는 two pointer dereferences를 수행해야만 한다는 것임.
  • vector의 indexed access는 오직 한 번 만 perform되는 것과 달리.

• deque의 storage는 자동으로 확장, 축소 가능하다.

  • std::vector에 대한 확장보다 비용이 적게 든다. 왜냐하면, std::deque의 확장은 "기존에 존재하던 elements를 new memory location으로 복사"하는 것은 하지 않기 때문이다.
  • 그런 반면, deque는 주로, 최소 memory cost자체는 큰 편이다.
    • 왜냐하면 just one element만을 가진 deque 역시 full internal array를 allocate해줘야만 하기 때문 (e.g. 8 times the object size on 64-bit libstdc++; 16 times the object size or 4096 bytes, whichever is larger, on 64-bit libc++).

• Front, Back에서의 insertion이나 beggining은 O(1) / 다른 elements는 선형 탐색하기 때문에 O(n)

• 역시 pop은 return void이기 때문에 , front(), back()을 통해 element를 return 받고 나서 pop 해야한다.

• front에 Firstly input한 element가 있고/ Back에 Last Input이 존재

백준 1021번

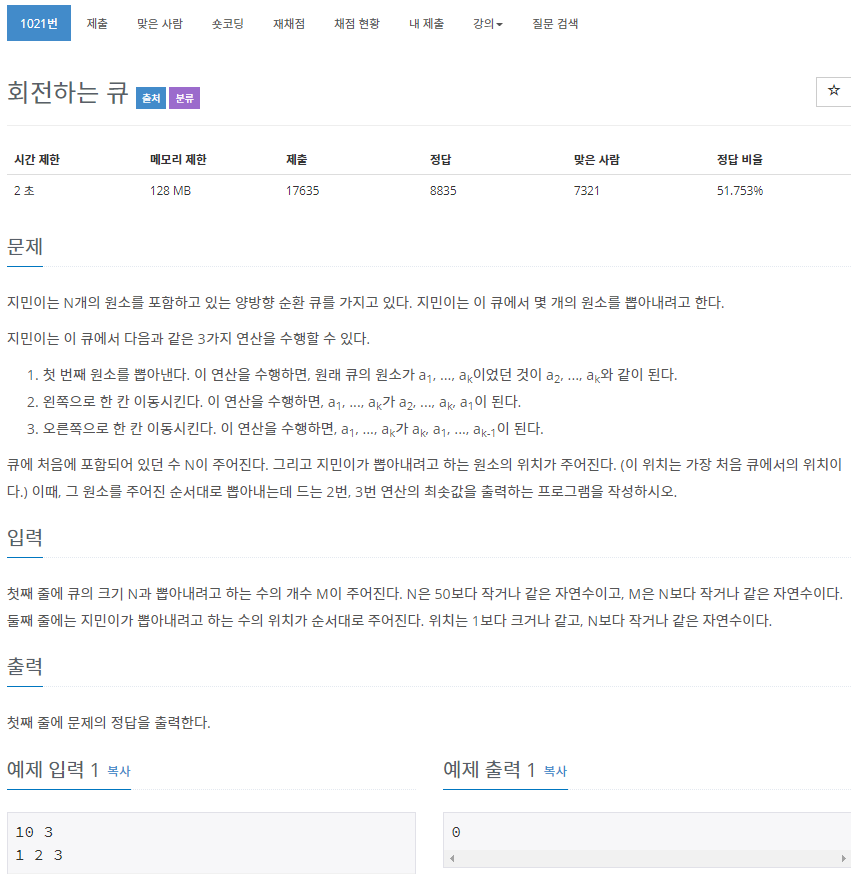
• 단순한 알고리즘 고민
  • greedy하게 풀어야 하는 걸까? 그니까.. 다음 순서를 위한 최소 연산을 택하면 되는 걸까???
    • 각 state마다 2번,3번의 연산자가 존재한다.
    • 만약 2 9 5 순서로 뽑아내려고 한다면, 2번 연산(2,3,4,5,6,7,8,9,10,1) → 1번연산 (3,4,5,6,7,8,9,10,1) → 3번연산(1,3,4,5,6,7,8,9,10)→3번연산(10,1,3,4,5,6,7,8,9)→ 3번연산(9,10,1,3,4,5,6,7,8)→1번연산(10,1,3,4,5,6,7,8) → 2번 or 3번연산을 4번 해서 2번or3번연산을 총 8번 하는 것이 최솟값.
    • 위의 방식을 할 때, 나는 각 state에서 다음 order를 위한 가장 최소의 방법을 택했음.
      • 이 문제는 이렇게 해도 될 거 같기 때문이다. Circular하게 돌아가고 있기 때문임.
    • 각 state에서 판단하기 : 두 가지 경우를 모두 해 보기 위해, q.at()을 사용하여 값을 확인한다.
• 구현 고민
  • cpp에는 deque STL이 존재함. 이를 이용

10 3
1 2 3
//0

10 3
2 9 5
//8

32 6
27 16 30 11 6 23
//59

10 10
1 6 3 2 7 9 8 4 10 5
//14
( 6 7 8 9 10 2 3 4 5) : 4 
(  7 8 9 10 2 3 4 5)
(3 4 5 7 8 9 10 1 2 ) : 3
(4 5 7 8 9 10 1 2 )
(2 4 5 7 8 9 10 1) : 1
(4 5 7 8 9 10 1)
(7 8 9 10 1 4 5 ) : 2 

#include<iostream>
#include <deque>

using namespace std; 
std::deque < int> q;
int n, m,my_c=0; // n : size of this queue . M : the number of elements which is intended to be extracted(operation 1) 
int order[50];

void operateTwo()
{
	// front에 있는 것을 Back으로 보낸다. 
	int front = q.front();
	q.push_back(front);
	q.pop_front();
	
}

void operateThree()
{
	// Back에 있는 것을 front로 보낸다. 
	int back = q.back();
	q.push_front(back);
	q.pop_back();
}

int solve(int target)
{
	int left_cnt = 0, right_cnt = 0;
	int i, j;
	// index는 항상 0에서부터 start. 
	// operation Two : 2번연산
	// operation three : 3번 연산 

	if (q.at(0) == target) {
		q.pop_front();
		return 0;
	}
	else {
		for (i = 1; i < q.size(); i++) {
			right_cnt++;
			if (q.at(i) == target) break;
		}
		for (j = q.size() - 1; j > 0; j--) {
			left_cnt++;
			if (q.at(j) == target) break; 
		}
	}
	// 현재 state에서 3번 연산으로 하는 경우, 연산의 횟수가 더 적은 경우 
	if (right_cnt > left_cnt) {
		for (i = 0; i < left_cnt; i++)
			operateThree();
		q.pop_front();
		return left_cnt;
	}
	else { // 2번 연산으로 하는 경우가 연산의 횟수가 더 적은 경우.
		for (i = 0; i < right_cnt; i++)
			operateTwo();
		q.pop_front();
		return right_cnt;
	}

}

int main()
{
	int i;
	cin >> n >> m; 
	for ( i = 1; i <= n; i++) {
		q.push_back(i);
	}
	// Target 집어 넣기. 
	for ( i = 0; i < m; i++)
		cin >> order[i];

	// Front element : 1,  Back : n 
	for (i = 0; i < m; i++) {
		int temp = solve(order[i]);
		my_c += temp;
	}

	cout << my_c << endl;

	

}