[백준]9184번

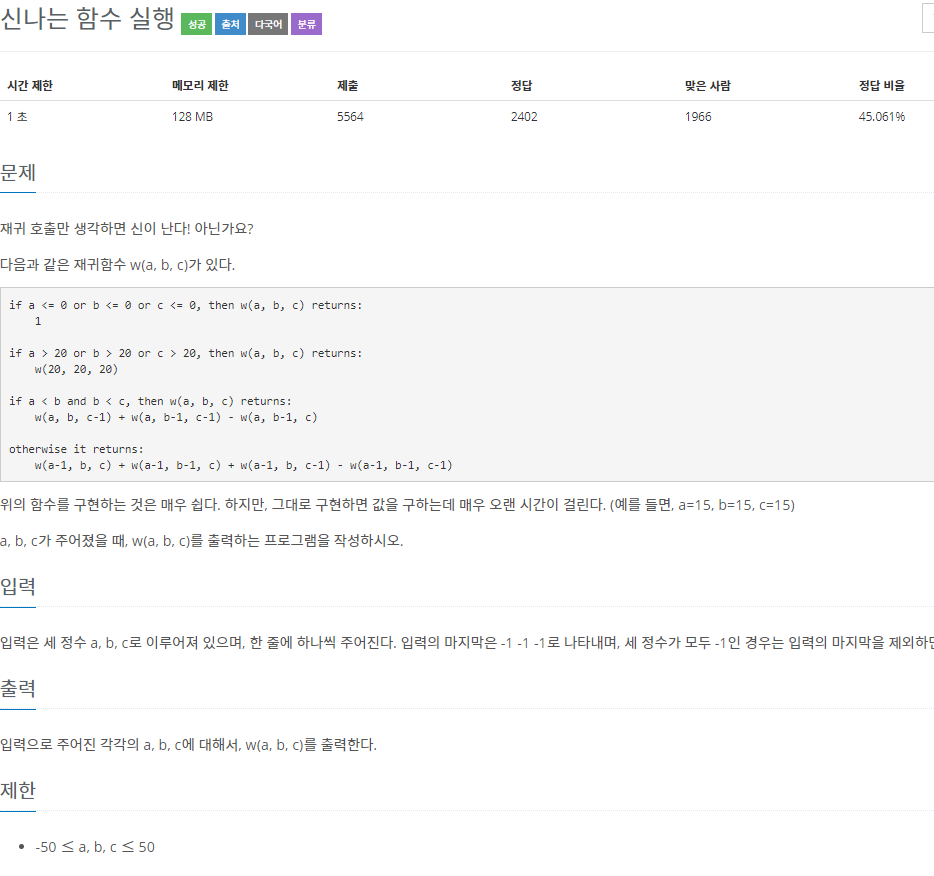
• 저런 식으로 정해진 규칙을 가진 재귀함수 형태가 나오는 문제의 경우, 다이나믹 프로그래밍 방식이 먼저 떠오르게 된다.
• 이제까지 풀어본 동적계획법 문제는 n 에 대한 식이었다. 이번에는 a,b,c라는 세개의 변수에 대한 것이었지만, 워낙 주어진 문제가 직관적이었어서 바로 동적계획법으로 풀었다.
• -50 <= a,b,c <= 50 이기에 입력으로 주어지는 (a,b,c) 전체 경우의 수는 약 1000000 이지만, 현재 재귀함수의 형태 상, 중복해서 호출하게 되는 (a,b,c)가 매우 많아지는 문제. (그래서 보통 이런 문제에서는 동적 계획법을 사용)
• (a,b,c,)
• 1. a or b or c가 0 이하 --> 무조건 return 1;
• 2. a or b or c가 20 초과 --> (20,20,20)
• 3. a<b<c 인 경우 w(a, b, c-1) + w(a, b-1, c-1) - w(a, b-1, c) 를 return
• 4. 나머지 경우 : w(a-1, b, c) + w(a-1, b-1, c) + w(a-1, b, c-1) - w(a-1, b-1, c-1)
• 재귀 호출을 하더라도 1을 return 하며 재귀호출에서 return 되오기 위해 , 재귀호출하는 파라미터는 '-' 만을 하고 있다.
• 보통 동적 계획법은 n 에 대한 dp 배열을 만들었다. 이 문제도 dp문제일까?
• a or b or c가 0이하인 경우는 항상 1을 return 하기 때문에 , 실질적으로 입력으로 주어지는 a,b,c 모두가 양수인 경우에 대해서만 고려하면 된다. AND . a or b or c가 20초과인 경우는 항상 a=b=c=20 일 때와 같기 때문에, 실질적으로 20 x 20 x 20 크기의 배열을 관리하는 것을 생각 해 볼 수 있다. 즉 8000가지의 경우를 for문을 돌려 먼저 채워 사용한다면 (bottom up방식의 ) 동적계획법 을 사용하는 것이 된다.
• dp가 갖는 값은 0보다 크다. 식 w(a, b, c-1) + w(a, b-1, c-1) - w(a, b-1, c) 와 w(a-1, b, c) + w(a-1, b-1, c) + w(a-1, b, c-1) - w(a-1, b-1, c-1)를 보니. 그리고 혹시나 하는 마음에 for문으로 출력 시 확인 가능.

#include <iostream>
#include <vector>

int a, b, c;
int dp[21][21][21]; // 각 row의 0번째 column은 사용 x  (a,b,c가 0보다크고 20이하인 경우만을 다룰 것이기에)
					// [a][b][c]


int w(int a, int b, int c)
{
	// 문제 상, dp가 갖는 값은 0이 아닌 값.(확인해봐야함) 
	if (a <= 0 | b <= 0 | c <= 0) return 1;
	else if (a > 20 | b > 20 | c > 20) return w(20,20,20);
	else if (dp[a][b][c]) return dp[a][b][c]; // 이곳에 위치하지 않으면 런타임 에러. dp배열은 0<a,b,c<=20 까지만을 다루고 있기 때문.
	else if (a < b & b < c) return (w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c));
	else return (w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1) - w(a - 1, b - 1, c - 1));
}

int main()
{
	int i, j, k,cnt=1;
	
	for (int i = 1; i < 21; i++) {
		for (j = 1; j < 21; j++) {
			for (k = 1; k < 21; k++) {
				dp[i][j][k] = w(i, j, k);
				
			}
		}
	}
	//a = 50, b = 50, c = 50;
	//printf("w(%d, %d, %d) = %d\n", a, b, c, w(a,b,c));
	///*
	std::cin >> a >> b >> c;
	while (!(a == -1 & b == -1 & c == -1))
	{
		printf("w(%d, %d, %d) = %d\n", a, b, c, w(a,b,c));
		std::cin >> a >> b >> c;
	}
	//*/
	
}

• 시간을 줄이기 위한 방법??