2024-05-28

안녕하세요 ~!
오늘은 팀편성이 시작돼서 새로운 팀원분들과 함께 지내봤습니다 !
그리고 학습주차이기 때문에
프로젝트 주차 때 이해하지 못했던 거나 까먹었던 것들
또또 복습해볼게요 😇
♾️ 상관관계
피어슨 상관계수 : 원래 값들 간의 직선적인 관계 측정
스피어만 상관계수 : 값들을 순위로 변환하여, 순위 간의 단조적인 관계 측정
켄달 상관계수 : 값들을 순위로 변환하여, 순위 간의 일치도를 더 세밀하게 측정
피어슨의 상관계수
두 변수 간의 선형적인 관계를 측정하기 위한 통계적인 방법
주로 연속형 변수(숫자)들 간의 상관관계를 평가하는 데 사용
- 범위 : -1에서 1 사이의 값
- 양의 상관관계 : 1에 가까울수록 강한 양의 선형관계
- 음의 상관관계 : -1에 가까울수록 강한 음의 선형관계
- 무상관 관계 : 0에 가까울수록 선형관계가 거의 없거나 약한 관계
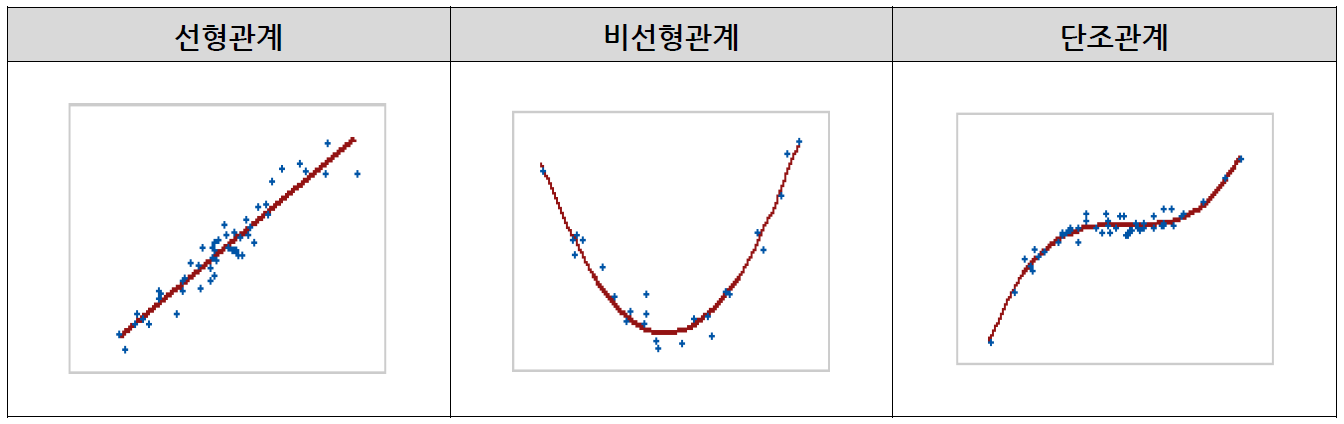
선형관계는 스캐터로 시각화하였을 때 올곧은 선 형태가 나타난다는 걸로만 참고해주시면 될 것 같네요 !
저번 프로젝트 주차 때 알았던 건데
치킨과 맥주의 상관관계는 0.8이라고 하네요 ,,
말했던 거라면 유감 ㅋ
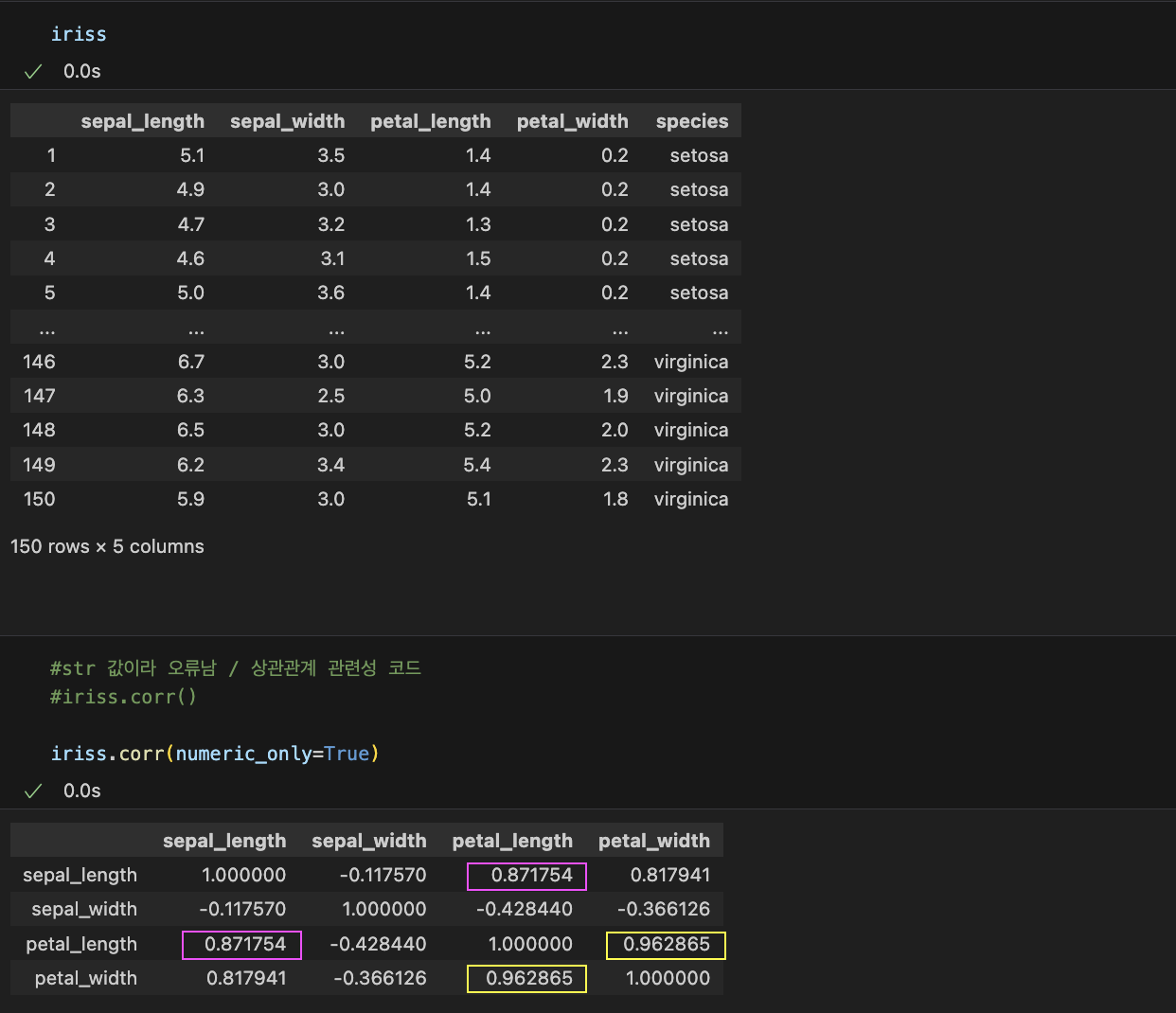
시본의 아이리스 데이터로 비교해보자면
iriss.corr(numeric_only=True)
숫자형 열들 간의 상관관계를 계산하는 명령어
피어슨 상관계수상관관계 행렬을 반환
numeric_only=True
숫자형 열들만 선택하여 상관관계가 계산되기 때문에 숫자형이 아닌 열들은 무시되고
오직 숫자형 열들 간의 상관관계만 계산
꽃받침 길이 | 꽃받침 폭 | 꽃잎 길이 | 꽃잎 폭
꽃잎 길이와 꽃잎의 폭 : 0.962865로 1에 가까운 숫자 - 강한 양적 선형관계
꽃받침 길이와 꽃잎 길이 : 0.871754로 1에 가까운 숫자 - 강한 양적 선형관계이렇게 상관계수를 알아보았는데요
이걸 시각화 해보자면 !!
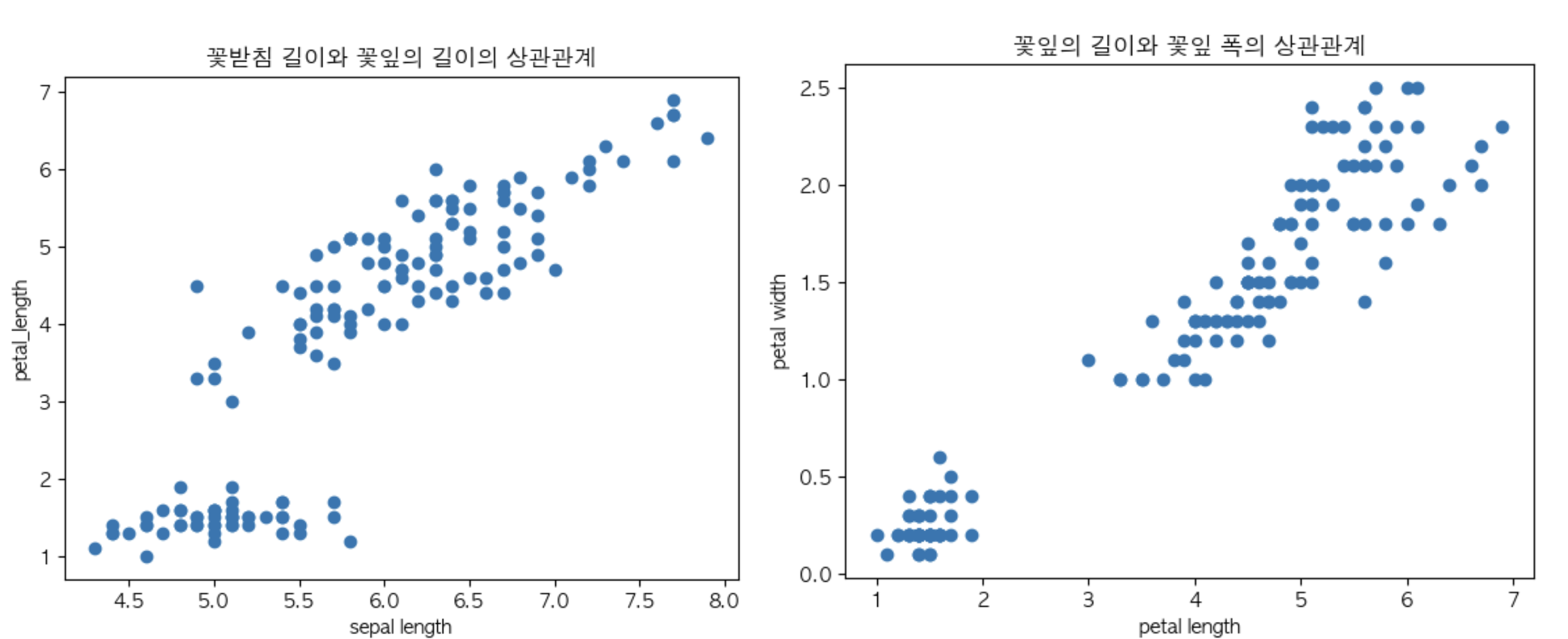
실제 두 변수 간의 상관관계가 1에 가깝기 때문에
맨 위에서 보았던 선형관계처럼 올곧은 형태인 걸 알 수 있습니다
그렇다면 반면에 가장 큰 음의 상관관계를 보였던(Sepal Width와 Petal Length의 상관계수: -0.428440)
꽃받침의 폭과 꽃잎의 길이는 그래프가 어떻게 나오는지 보여드릴게요 !
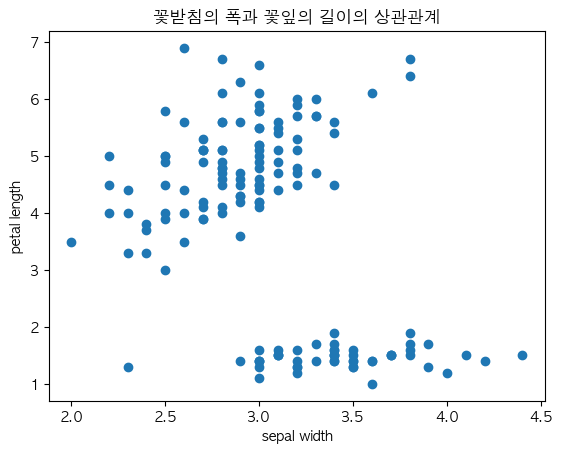
위 양의 상관관계를 띄는 그래프와 전혀다르게
올곧지 않고 오히려 정반대에 가까운 수준인 걸 알 수 있죠 !!
🔥 이쯤에서 내가 이해 안돼서 다시 쓰는 말
'상관관계'와 '상관계수'의 차이는 ,,,?
상관계수는 선형 관계의 강도와 방향을 측정하는 수치
상관관계는 상관계수를 시각적으로 표현
이를 통해 두 변수 간의 패턴이나 트렌드를 시각적으로 이해할 수 있다.
상관관계는 개념적인 측면에서 이해할 수 있는 변수 간의 관계를 나타내고,
상관계수는 이러한 관계를 수치적으로 측정하여 분석할 수 있도록 도와줍니다.
어렵다고 생각되신 다면 아주아주 쉽게 말해볼게요
'상관관계'는 그냥 개념일 뿐인데 이걸 시각화할 때 '상관계수'를 사용한 것임.
그렇기 때문에 '상관관계'가 개념이지만서도 시각화(시각화를 할 수 있게 수치로 사용된 게 '상관계수')된 자료가 포함된 것임.
이해가 될진 모르겠지만,, 그냥 저 이해하려고 쓴 말 입니다 ^~^
♾️ 사분위수
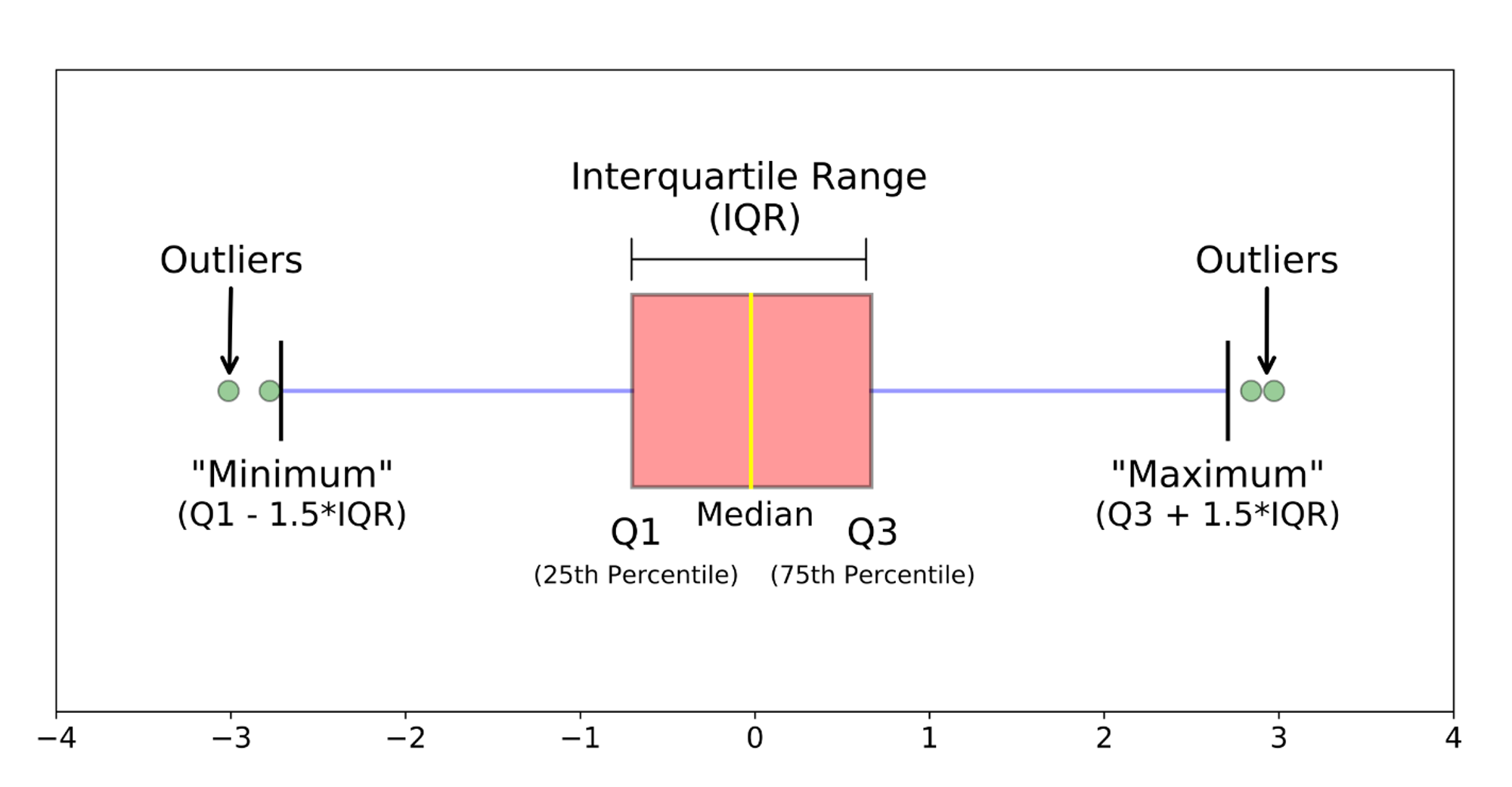
Q1 (0% - 25%): 하위 25%의 데이터
Q2 (25% - 50%): 25%에서 50% 사이의 데이터 (여기서 Q2는 중앙값, 즉 전체 데이터의 중간)
Q3 (50% - 75%): 50%에서 75% 사이의 데이터
Q4 (75% - 100%): 상위 25%의 데이터
중앙값 (Q2)
|
|
v
|---------------------|
Q1 | Q2 | Q3
25% | 50% | 75%
<------>|<------------------>|<------->
구간 표시:
Q1: 0% - 25% (하위 25%)
Q2: 25% - 50% (중간 하위 25%)
Q3: 50% - 75% (중간 상위 25%)
Q4: 75% - 100% (상위 25%)
각 사분위수의 위치를 포함한 상자 그림:
중앙값 (Q2)
|
|
v
Q1 |---------------------------------| Q3
25% | Q2 | 75%
(데이터의 하위 25%) |------------------------------------| (데이터의 상위 25%)
-3 -2 -1 0 1 2 3
설명:
- Q1 (제1사분위수): 데이터의 하위 25%를 구분하는 값
- Q2 (중앙값, 제2사분위수): 데이터의 중앙값
데이터의 50%가 이 값보다 작고, 나머지 50%가 이 값보다 크다
- Q3 (제3사분위수): 데이터의 상위 25%를 구분하는 값
Q4(Q3보다 큰 데이터로, 이는 상위 25%를 차지)는
사분위수라기보다는 데이터의 전체 범위를 네 구간으로 나눈 마지막 구간을 의미합니다 !!
이렇게 오늘은
이해가 안됐던 용어들을 위주로 다시 복습해봤습니다 ㅎㅎ
코알못이라 설명이 상당히 허접한 점 양해드리고요 ,,
아니? 사실 내가 기억하려고 허접하게 적음
내일은 통계학 강의로 돌아오겠습니다 !!
오늘도 고생하셨어요 🍀
