이 논문은 수학 문제 풀이 과정 채점해주는 PRM(progress reward model)모델 MATH-SHEPARD 제작기를 다루고 있다.
특히, human-annotated 데이터셋 없이 LLM을 이용해 PRM을 훈련시킬 데이터를 만든 과정을 설명한다.
이전 연구
복잡한 수학문제를 푸는 것은 LLM의 오래된 과제이다. Pre-training, fine-tuning, 그리고 verification이 사용되어 왔다. 그중에 verification을 연구하게 된 동기는, top-1 결과가 언제나 제일 좋은 결과는 아니라는 것이다. Verification 모델은 후보 답변들을 재랭킹하면서, LLM 결과의 정확도와 일관성을 올릴 수 있다.
Verification model들을 outcome reward model(ORM)과 progress reward model(PRM)으로 나눌 수 있는데, ORM은 최종 답변을 갖고 답변을 예측하는 반면 PRM은 step-by-step 추론 과정을 evaluate한다.
PRM이 여러모로 더 선호되는데, 첫번째 이유는 오류의 정확한 위치를 알려주므로써 섬세한 피드백이 가능하다는 것이다. 이는 강화학습과 자동 correction에 중요하다. 또한, 만약 풀이 과정에서 오류가 났다면, 답변에도 오류가 날 확률이 높다.
그러나 PRM을 학습할 데이터를 모으는 것은 아주 힘든 과정이다. Human annotator들이 단계별로 annotate를 하는 방식으로 모아왔지만, 실력있는 annotator들을 모아 데이터를 생성하는 것은 꽤나 비싸다.
그러므로 이 논문에서는 자동적인 annotation framework를 제작하였다.
Methodology
Reward model의 성능을 두가지 시나리오를 통해 검증하였다.
- Verification: 문제 p가 주어졌을 때, 후보 답변 N개를 생성하고 reward model을 통해 답변들을 랭킹하도록 한다. 최종적으로 가장 높은 점수를 가진 답변이 최종 답변으로 선택된다.
- Reinforcement Learning: PRM을 사용하여 단계별 PPO를 통해 LLM을 지도한다.
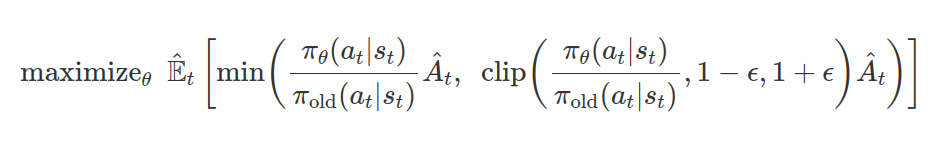
이때 PPO란 주어진 데이터를 갖고 현재 policy를 향상시키면서, 이전 policy와 너무 크게 업데이트되어 발산해버리는 것을 막는 것이다. KL divergence를 사용하여 계산했던 TRPO와 달리 clipping 방식으로 일차미분법을 사용하는 메서드로 변경하여 계산량을 줄였다.
reward model는 ORM과 PRM으로 나뉜다.
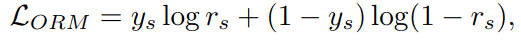
만약 s(답변)가 정답이면 y_s는 1이고, 아니라면 y_s는 0이다. r_s는 ORM으로부터 설정된 s의 sigmoid이다. 즉 0~1 사이에서 s가 정답일 가능성이다.
이를 통해 모델은 더 나은 솔루션을 선택하도록 학습한다.
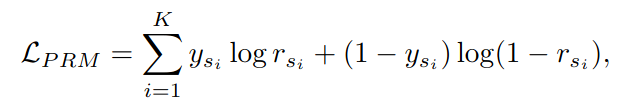
PRM은 답변의 각 단계 evaluation을 학습한다. y_si는 s_i(답변의 i번째 단계)의 정답유무 레이블이다. Good, neutral, bad 총 세가지로 나누어서 학습할 수도 있는데 별 차이가 없어서 그냥 binary로 했다고 한다.
각 추론 단계의 퀄리티는 올바른 답을 도출할 가능성으로 계산했다. 이는 ORM과 비슷하게 noise가 있을 수 있지만, PRM을 잘 학습시킨다고 한다.

즉 추론 과정과 답변까지 만든 다음, 각 추론 과정을 답변의 정답률로 점수를 계산한다.
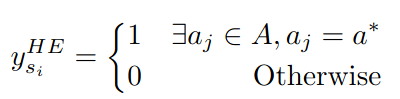
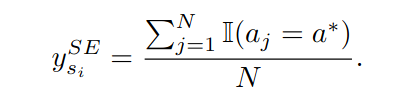
이때 점수는 hard estimation과 soft estimation으로 나뉘어 전자는 답변의 정답 유무, 즉 0과 1로 계산하고 후자는 맞는 답변으로 향하는 frequency로 계산한다.

또한, 이전에 말했던 verification을 위한 랭킹은 후보 답변이 N개의 후보군에서 얼마나 자주 등장했는지(self-consistency)와 해단 솔루션이 reward model에게서 받은 점수를 결합하여 최종 점수를 계산한다.
