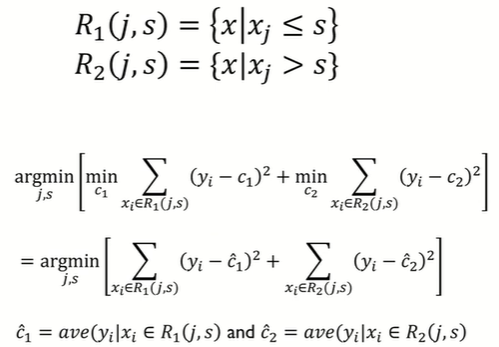[의사결정나무]

의사결정나무 모델

• 데이터에 내재되어 있는 패턴을 변수의 조합으로 나타내는 예측/분류 모델을 나무의 형태로 만드는 것

Algorithm

• 데이터를 2개 혹은 그 이상의 부분집합으로 분할
  -> 데이터가 균일해지도록 분할
• 균일의 정의
  • 분류: 비슷한 번주를 갖고 있는 관측치끼리 모음
  • 예측: 비슷한 수치를 갖고 있는 관측치끼리 모음

Model

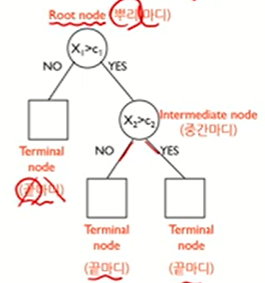
이진분할

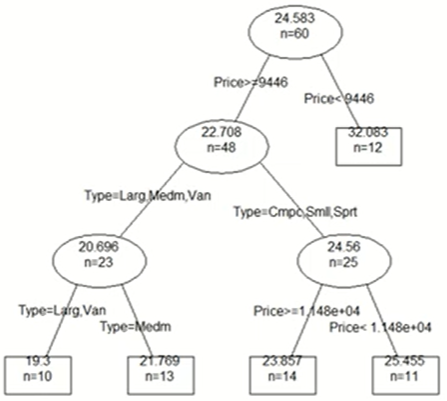
• 끝마디에 있는 n을 합치면 뿌리 개수가 된다
  
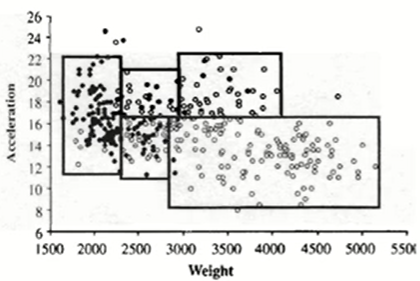
• 나눔으로써 균일해짐
  
• 부분 집합과 끝마디 개수가 같다.
• 트리에서 D, E, C 3개의 끝마디가 있는데 그래프에서 3부분으로 나뉘어 있다.

예측나무 모델(Regression Tree)

• 예측나무 모델에서 Y는 숫자이다.
  
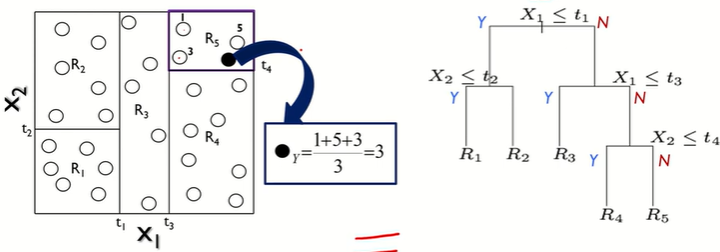
• 점들은 하나하나 Y값을 가지고 있다.
• 같은 부분집합의 다른 점 Y값의 평균으로 예측하겠다.
• 두 그림은 형태는 다르지만 같은 내용이다. 트리의 끝마디개수와 부분집합 개수가 같다. 왼쪽 그림의 R2에 6개의 점이 있으므로 R2에는 6개 데이터가 있음을 알 수 있다.
  
• $I{(x_{1},x_2)\in R}: x_1, x_2가 R_m지역에 있나?$
• $R_m은 끝마디$
• $R_3에 있으면: C_1 \times 0+C_2 \times 0+C_3 \times 1+C_4 \times 0+C_5 \times 0 = C_3$
  
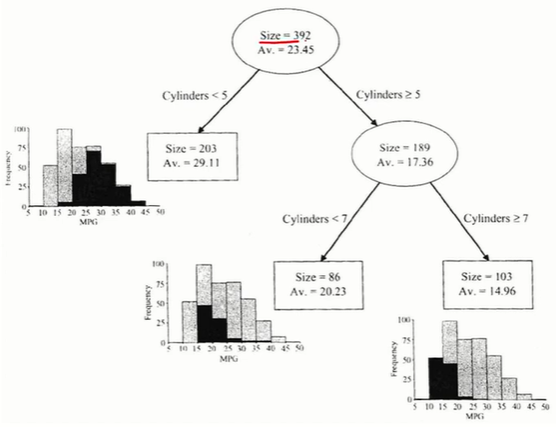
• size: 관측치 개수
• AV: Y out의 평균

예측나무 모델링 프로세스

• 데이터를 m개로 분할(끝마디가 m개): $R_1, R_2,...,R_m$
  $\displaystyle\sum_{m=1}^{M}{C_{m}I(x)\in R_m}$
• 최상의 분할은 cost function을 최소로 할 때 얻어진다.
  $\min_{C_m}\displaystyle\sum_{i=1}^{N}{\{y_i-f(x_i)^2\}}$
• 각 분할에 속해 있는 y값들의 평균으로 예측했을 때 오류가 최소
  

분할변수(i)와 분할점(s)은 어떻게 결정할까?

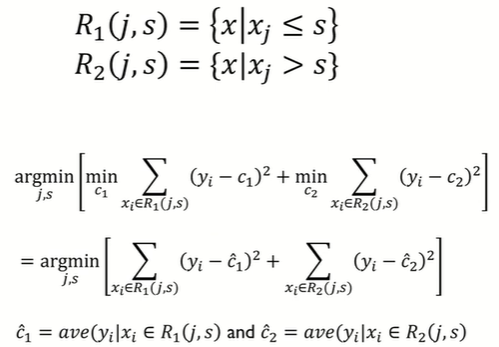
• 모든 고려사항을 다해보고 가장 최소화 되는것을 i,s로 정한다.

분류나무 모델

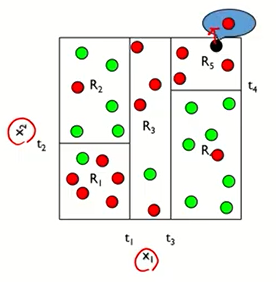
• 빨강색과 초록색을 균일하게 나눔
• 빨강색 범주인지 초록색 범주인지 분류해야함
  ex) R5에 새로운 점이 들어왔다면 주변 점들의 평균을 통해 빨강색이라고 예측가능하다.
  ex) R2에 새로운 점이 들어왔다면 주변 점들의 평균을 통해 초록색이라고 예측가능하다.
  
• $R_m$: 끝노드, $N_m$ 끝노드에 있는 관측치 개수
• 해당 끝 노드에 있는 모든 관측치 중에 첫번째 클래스에 해당하는것이 몇개 있는지 비율을 보는것
• 끝노드에 1 1 1 0 0 이 있다면: $P_{11}=3/5, P_{12}=2/5$
• 끝노드 m으로 분류된 관측치는 k(m) 클래스로 분류
  3개 class $P_{11}=0.6, P_{12}=0.3, P_{13}=0.1$
  = argmax(0.6, 0.3, 0.1)
  = 1: 0.6의 class명
  
  ex) $x_1, x_2 -> R_3 이면 f(x)=k(3)가 된다.$
  k(3)가 의미하는 것은 R3에 가장 많은 클래스 비율을 차지하고 있는 k (=k(3))로 output 할것이다.

분류나무 모델링 프로세스

• 비용함수가 3개 있다.

분할변수(j)와 분할점(s)은 어떻게 결정할까?

• 비용함수를 최소화하는 j와 s

분할법칙

• 불순도의 감소가 최대가 되도록

분류나무 모델링 프로세스

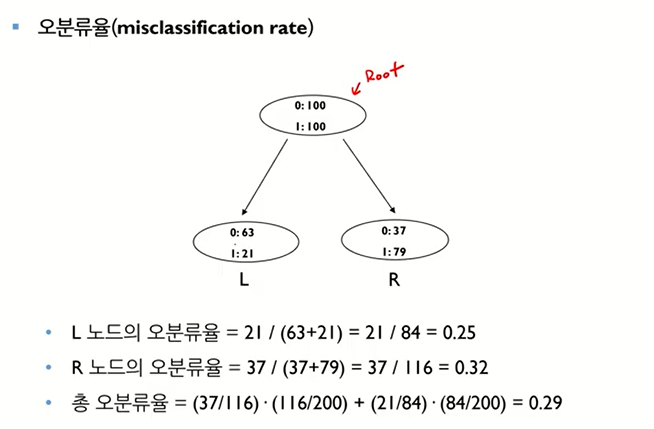
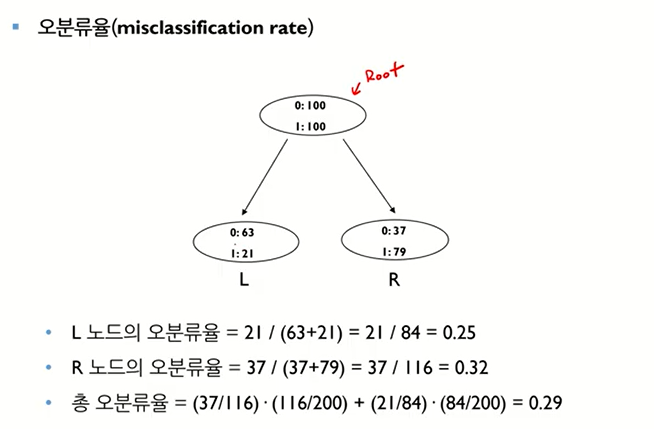
• L은 대다수가 0이기 때문에 0으로 분류, R은 대다수가 1이기 때문에 1로 분류

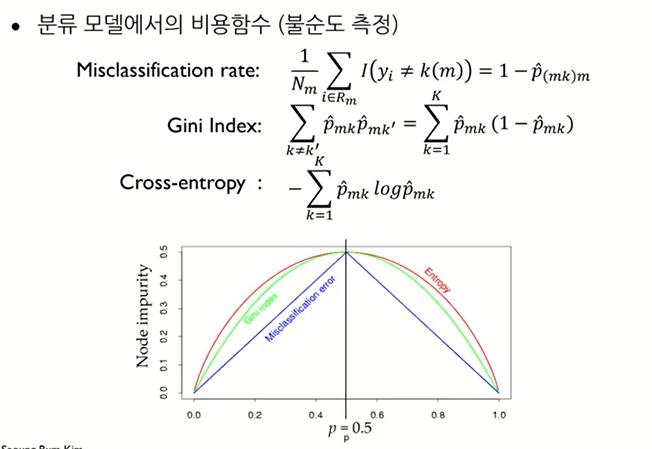
Gini와 entropy

• 얼룩말 6마리, 코뿔소 1마리일 때
• p1 = 얼룩말일 확률 = $6/7$
• p2 = 코뿔소일 확률 = $1/7$

개별 트리 모델의 장점

• 계층적 구조로 인해 중간에 에러가 발생하면 다음 단계로 에러가 계속 전파
• 학습 데이터의 미세한 변동에도 최종 결과 크게 영향
• 적은 개수의 노이즈에도 크게 영향
• 나무의 최종 노드 개수를 늘리면 과적합 위험(low bias, large variance)
• 해결방안 -> Random forest