1. 베이즈의 정리

조건부 확률을 구할 수 있는 대상으로 조건부 확률 구조를 변환

ex)

결론)

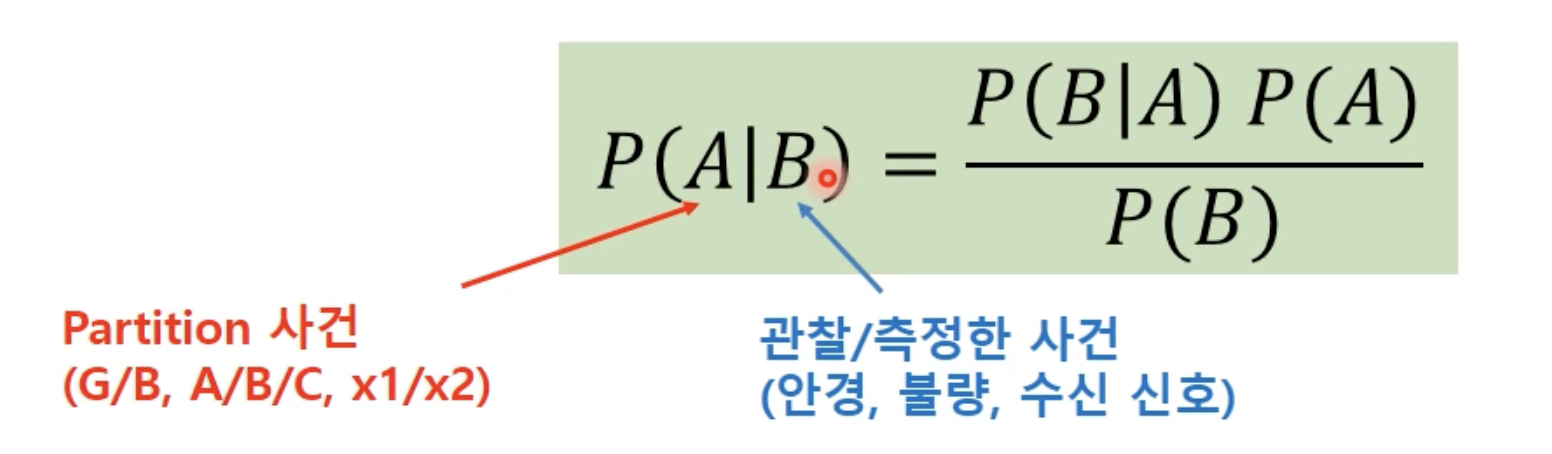
🏷️ 파티션에 해당하는 사건이 조건으로 주어지면 조건부 확률을 쉽게 구할 수 있다.
하지만 반대로 조건이 파티션이 아닌 경우, 직접 계산이 어려워 베이즈 정리를 사용하는 것이 일반적입이다.
❗️이때 조건이 파티션이 아닌 경우 = 관찰/측정한 사건(안경/불량/수신 신호)이 조건인 경우

2. 베이즈 추정

추정 (Inference - 추론)

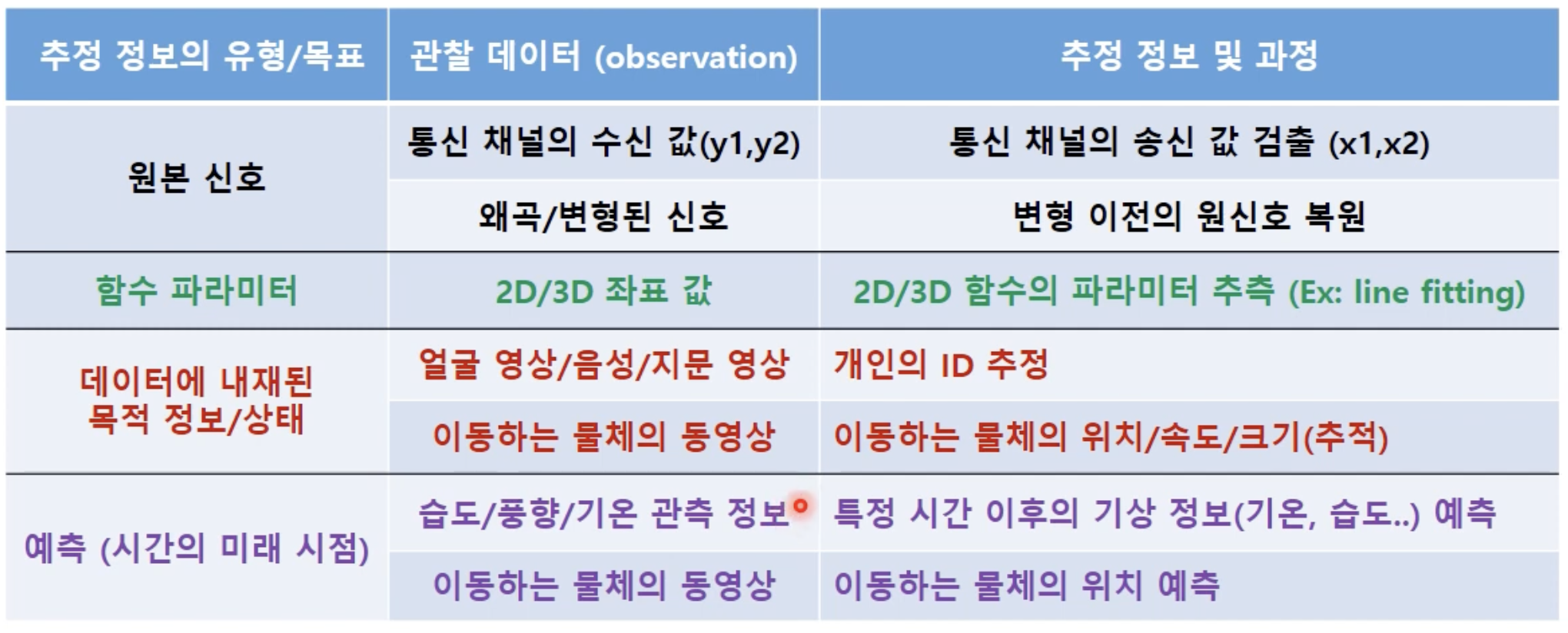
주어진 관찰 데이터(observation)로부터 어떤 정보를 구하는

확률적 접근 방법

1. 정보 신호를 확률변수로 설정하여 확률 분포를 분석 or 확률분포함수로 모델링
2. 일반적으로 최대 확률을 갖는 정보 값을 추정의 결과로 선택

확률적 estimation 방법

Likelihood (=조건부 확률)

• 사전 학습과 관찰을 통해 얻은 데이터 - 정보 간의 특징, 또는 (조건부)확률분포
• 주어진 데이터와 정보 값 간에 유사한 정도를 비교하는 기준
  ex) 머신러닝/인공지능 딥러닝 학습에 의한 출력

Prior

• 추정 대상인 정보 신호 자체의 사전정보, 확률분포
• 추정할 때 바람직하게 적용하는 정보의 특징 또는 (제한)조건
• observation에 대한 정보가 아님!
• prior 값을 선정하는데 절대적인 규칙은 없음
  

1. Maximum Likelihood estimation (MLE)

• Liklihood가 최대화하는 값을 찾는 방법
  

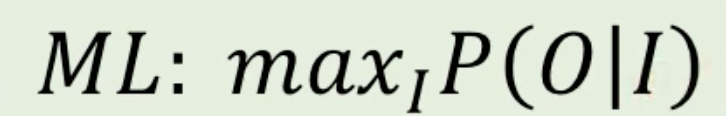
2. Maximum A Posterior (MAP) estimation -> Baysian estimation

• 베이즈 추정은 likelihood와 prior의 product로 확률을 계산해서 사용
  
  

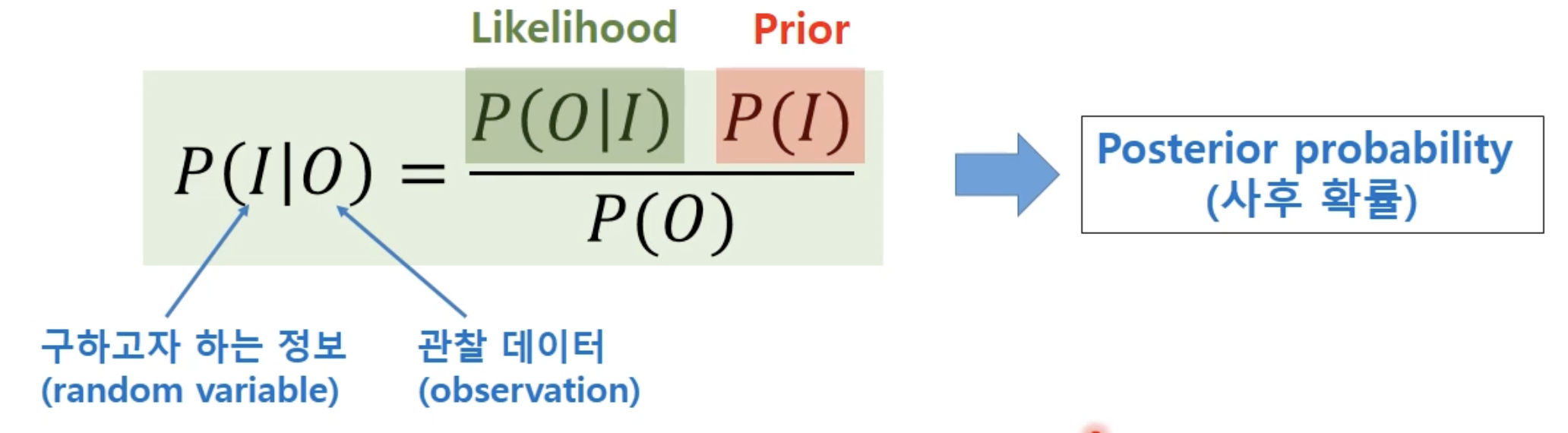
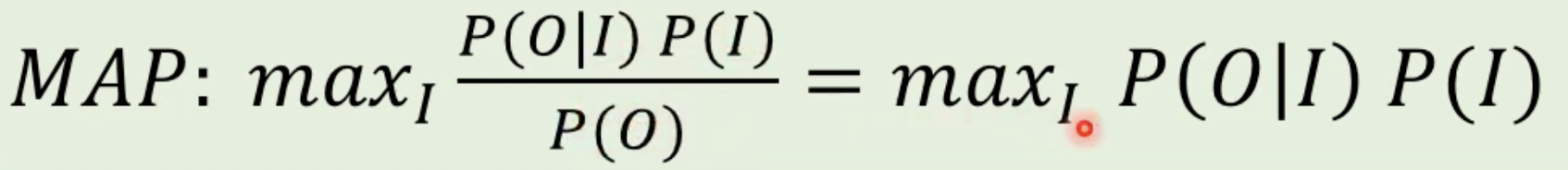
ex)

❗️일반적으로 map estimation을 사용하는 것이 성능이 개선됨, 적절한 prior 설정이 중요!