누적분포함수 - Cumulative Distribution Function(CDF)

• 확률 변수가 특정 값 이하일 확률을 나타내는 함수, 특정 값까지의 확률을 누적해서 더한 값
• 특정 값은 sample space에 없는 값도 가능
• non-decreasing function (x1 < x2, then F(x1) <= F(x2))
• 
• 

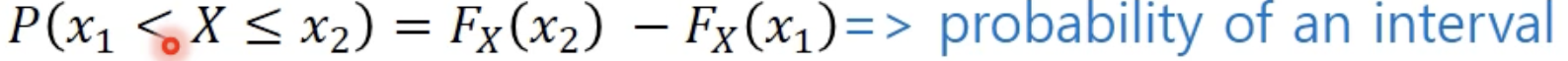
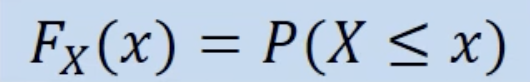
1. 이산확률변수

확률질량함수(PMF)

이산확률변수 = x가 특정한 값을 가질 때, 해당 값들에 대한 확률이 존재
이를 확률분포로 나타내면 = 확률질량함수

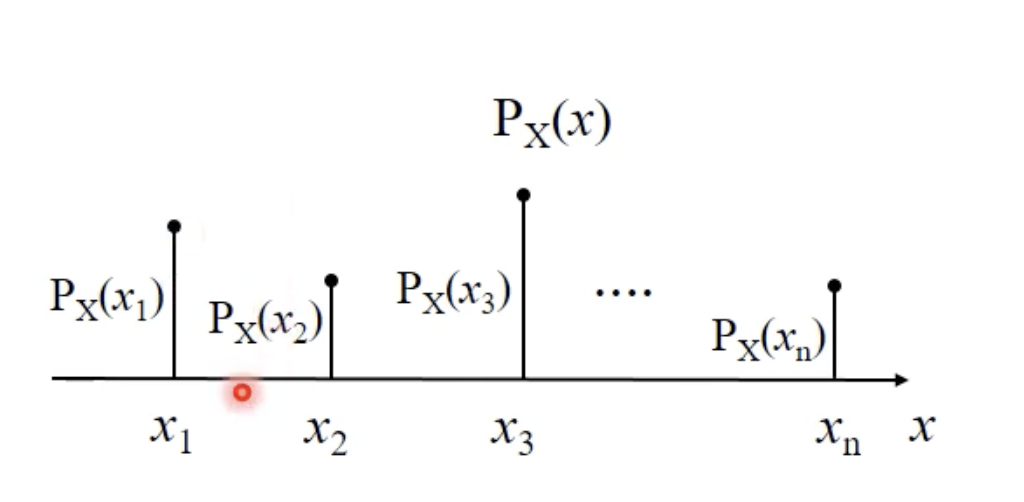
특징

• discontinuius, 연속적이지 않고 특정한 점에서만 값을 가짐
• 델타 함수(특정한 점에서만 값을 가지는 함수)들의 합으로 나타냄

CDF of 이산확률변수

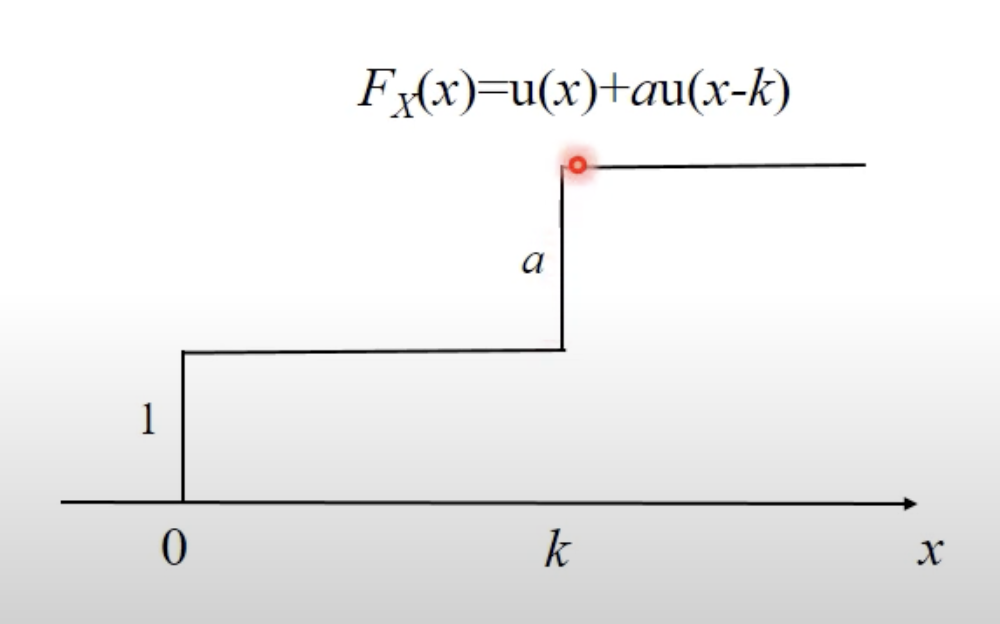
특징

• step 함수들의 합으로 나타냄
• 이산확률변수나 연속확률변수에 상관없이 연속 함수로 정의

2. 연속확률변수

확률밀도함수(PDF)

연속확률변수 = x가 특정 구간 내에서 셀 수 없이 많은(uncountably infinite) 값이 존재
이를 확률분포로 나타내면 = 확률밀도함수

특징

• 연속확률변수에서 특정한 하나의 값에 대한 확률은 항상 0에 수렴
  (무한한 값을 가질 수 있으므로, 특정 하나의 값이 나올 확률이 0임)
• 특정한 하나의 값에 대해 확률이 아니라,구간을 기반으로(밀도) 나타냄
• CDF를 이용하여 연속확률변수의 확률분포 = 확률밀도함수를 나타냄
• 
• 
• 

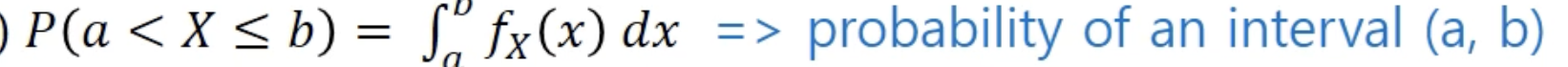
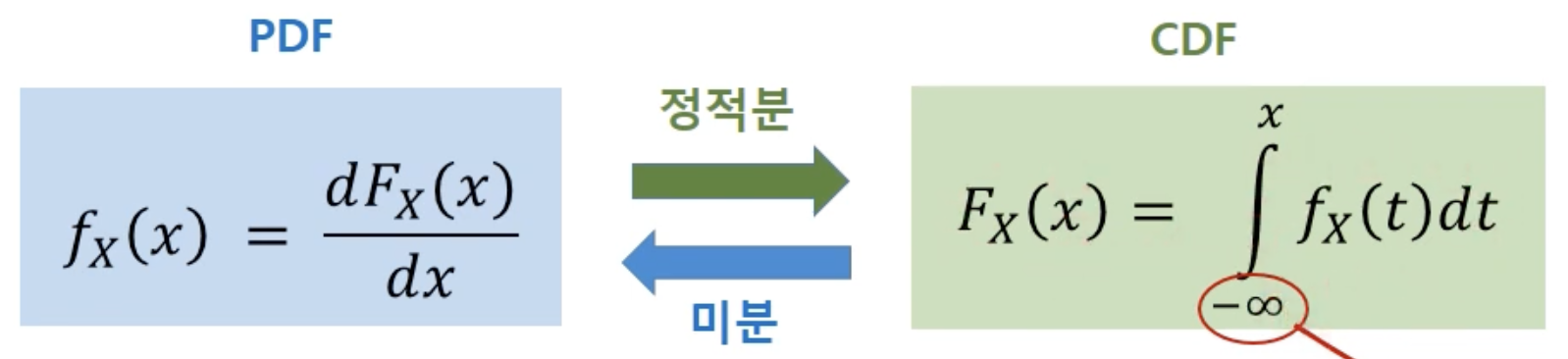
🏷️ 연속확률변수라 하더라도 이산확률변수로 양자화하여 적용
(양자화: 일정한 작은 간격 단위로 구간 설정 -> 히스토그램)