반갑습니다.
Activation function에 대해 얘기해보겠습니다.
Activation function(활성화 함수)가 뭐에요?
Activation fuction(활성화 함수)는 모델에 비선형성을 추가하여 복잡한 패턴이나 표현을 학습하고 표현할 수 있도록 돕는 함수입니다. 모델이 비선형성을 갖지 못한다면 단순한 패턴만 표현할 수 있기에 아주 중요한 부분입니다.
활성화함수의 설명에 대해 읽어보면 살짝 와닿지 않을 수도 있습니다.
비선형성을 어떻게 추가한다는 것일까요?
만약 선형 함수만을 사용하여 모델을 제작하였다고 생각해봅시다.
모델의 출력은
와 같이 하나의 선에 대입하는 방법으로 표현되겠죠.
그렇다면, 결국 input의 증가에 따라 output도 증가하고, input의 감소에 따라 output도 감소를 하는 하나의 선으로서 표현됩니다.
하지만 우리가 기대하는 출력값이 곡선의 형태를 띄고 있다면, 우리의 모델은 직선만 표현하므로 비슷한 형태를 출력할 수 없습니다.
이를 막기위해 으로 나온 출력값에 선형성을 띄지 않는 함수를 넣는 것입니다.
다음은 비선형 함수의 종류들입니다.
Sigmoid
고전적인 활성화 함수입니다. 뒤에 설명할 문제(Vanishing Gradient) 때문에 요즘에는 자주 사용되지 않습니다.
Tanh ( Hyperbolic Tangent )
Sigmoid의 업그레이드(?) 버전입니다.
기울기가 더 가파르기 때문에 학습이 빨리 되고, Sigmoid 함수와 다르게 음수의 값을 가질 수 있어 기울기 편향을 막습니다.
ReLU
Vanishing Gradient를 거의 해결할 수 있는 활성화 함수입니다. 대부분의 학습을 잘 이루어지게 하며, 요즘의 활성화함수는 대부분 ReLU함수의 개선버전이라고 생각합니다.
Softmax
Softmax 함수는 모델의 출력값들을 0과1사이의 확률값으로 변환해주는 역할을 합니다.
주로 MLP의 끝단에서 output이 어떤 label을 가지고 있을지에 대한 확률을 얻고 싶거나 transformer의 구조에서 사용됩니다.
Leaky ReLU
는 0.01과 같은 작은 값을 사용 )
ReLU 함수가 0보다 작은 값에서는 0을 반환하기에, 음수값을 조금은 살리고자 0이하의 값에서 살짝의 값을 반환하도록 조정한 함수입니다.
ELU
Leaky ReLU나 ReLU들은 기울기가 고정되어 있기 때문에 누가봐도 뭔가 잘못된 값이 입력됐을 때 기울기를 반환합니다.
이를 막기 위해 곡선 형태로 이상치의 입력을 깔끔하게 커버할 수 있는 함수가 ELU입니다.
이 외에도 Swish, GELU와 같은 다양한 활성화함수들이 존재합니다.
모두 목적은 비선형성을 추가하는 것인데, 왜 이리 종류가 많을까요
그 이유는 Vanishing Gradient problems에 있습니다.
Vanishing Gradient가 뭐에요?
기울기 소실 문제라고도 불리는 Vanishing Gradient는 기울기가 MLP의 층이 깊어질수록 소멸(아주 작은 값에 수렴)하는 문제입니다.
MLP는 오차 역전파 방법으로 로스와 예측값의 차이를 앞단의 파라미터까지 전달합니다. 그 과정에서 활성화 함수의 미분값 또한 곱하는 과정이 생기는데, 이 때 활성화 함수가 적절한 형태를 가지고 있지 않으면 제일 앞단에는 기울기값이 거의 0에 수렴하여 학습을 제대로 하지 못하게 됩니다.
이해를 돕기 위해 그림을 보겠습니다.
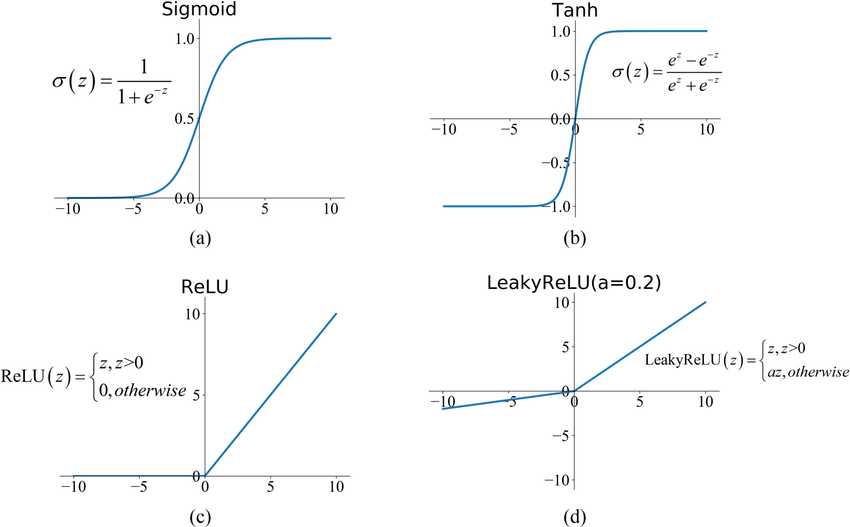
여기서 sigmoid와 Tanh의 그림을 보면, 양 끝단으로 갈 수록 접선의 기울기(미분값, grad)가 거의 0입니다.
우리의 모델이 층이 아주 깊고, 학습을 하던 중 어떤 값 하나라도 두 활성화함수 양 끝단의 grad가 곱해지면 거의 0에 가까운 값이 나오겠죠.
학습이 불안정하다는 의미입니다.
그 뒤로부터 나오는 ReLU, LeakyReLU, GELU 등은 전부 비선형성을 추가하면서 학습을 안정적이면서 잘되게 하기 위해 등장한 함수들입니다.
혹시나 모델을 구현하면서 뭔가 렐루의 발음인데 살짝 다르다 싶으시면 ReLU의 아들이구나 생각하시고, 구글에 그래프 한번 보시고 사용하시면 되겠습니다.
