반갑습니다.
Tensor의 norm에 대해 얘기하고자 합니다.
고딩시절 배웠던 기하와벡터가 떠오르네요. ㅎㅎ
노름(norm)이 뭔가요?
노름(norm)이란, 벡터에 크기를 부여하는 함수입니다.
저는 이번 글에서 L1 norm, L2 norm, L∞ norm 세가지에 대해 설명해보겠습니다.
norm의 식은 다음과 같습니다. 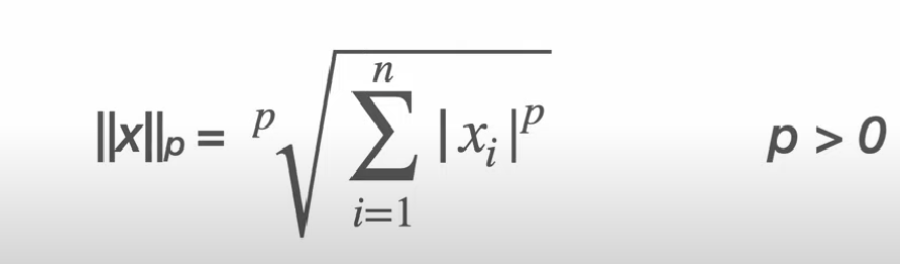
p 에 1을 넣으면 L1 norm, 2를 넣으면 L2 norm, 무한대를 넣으면 L∞ norm이 됩니다.
예를 들어서, vector([1,2,3,4])가 있다고 치면 ,,
p = 1 일 때는 10
p = 2 일 때는 루트 30
p = ∞ 일 때는 4가 나옵니다. 극한으로 보시면 돼요.
그럼 이 노름을 어따 쓰느냐
그건 저도 유사도에 쓰인다는 거 말고는 잘 모릅니다. 감사합니다.
L1, L2 정규화에 쓰이는 것도 알고는 있는데 설명할 정도로 알지는 못합니다. 나중에 더 보강해서 설명해보겠습니다.
유사도는 멘헤튼 유사도, 유클리드 유사도가 있는데, p 가 뭐냐에 따라 이름이 달라집니다.
p = 1 일 때는 멘헤튼 유사도이고, p = 2 일 때는 유클리드 유사도라 부릅니다.
유사도란 두 벡터가 얼마나 비슷하냐를 의미하는 수치라고 보시면 됩니다.
공식은 간단합니다.
shape이 같은 두 벡터를 빼고 역수를 취하면 됩니다.
이 때 두 벡터가 똑같으면 norm이 0이 나오는데, 이러면 분모에 0이 드가니까 1을 더해줍니다. 그러면 최대값이 1이 나오는거죵
토치에서는 감사하게도 norm을 구하는 코드가 있으니, 한번 예제를 살펴보겠습니다.
제가 공부할 때는 찾아볼 때 설명은 대충 읽고 항상 예제부터 봤었기에 저같은 사람이 또 있을수도 있음을 염두하여 예제를 자주 넣고 싶습니다.
import torch
a = torch.tensor([1,2,3,4,5], dtype = torch.float32)
b = torch.tensor([5,4,3,2,1], dtype = torch.float32)
print(torch.norm(a, p = 1))
print(torch.norm(a, p = 2))
print(torch.norm(b - a, p = 1))
print(torch.norm(a - b, p = 2))
def save_similarity(d, p):
d = torch.norm(d, p = p)
simil = 1 / (d+1)
return simil
print(save_similarity(a-b, 1))
print(save_similarity(a+b, 1))
>>tensor(15.)
tensor(7.4162)
tensor(12.)
tensor(6.3246)
tensor(0.0769)
tensor(0.0323)뭐 이런식으로 수학 공식을 고대로 넣어서 구해보시면 될 거 같습니다.
a,b의 유사도는 유클리드 유사도냐 멘헤튼 유사도냐에 따라 값이 달라지는군요.
유클리드 유사도는 점과 점 사이의 직선을 쭉 이어서의 거리이고, 멘헤튼 유사도는 약간 골목길 가듯이 상하좌우 이리저리 이어서 가는 거리를 의미합니다.
유사도는 이 외에도 많습니다.
그중 코사인 유사도에 대해서 설명해보겠습니다.
고딩시절 기하와 벡터에서 내적을 배우는데요.
공식을 보시면 ABcos(Θ)입니다.
이거를 좀 더 살펴보면
직선 A와 직선 B가 있고, 그중 한 선을 나머지 선에 사영하는겁니다.
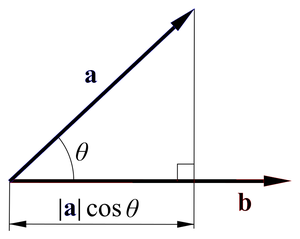
(출처 : 위키독스 )
다들 아시겠지만 아는척좀 해봤습니다.
아무튼 한 선에 맞춰서 사영을 해보면 각에 따라 절대적인 크기보다 작게 나오겠죠
이것을 활용한 유사도입니다.
import torch
a = torch.tensor([1,2,3,4], dtype = torch.float32)
b = torch.tensor([-1,-4,-12,0], dtype = torch.float32)
c = torch.tensor([1,2,3,4], dtype = torch.float32)
print(torch.dot(a,b) / (torch.norm(a, p = 2) * torch.norm(b, p = 2)))
print(torch.dot(a,c) / (torch.norm(a, p = 2) * torch.norm(c, p = 2)))
>>tensor(-0.6475)
tensor(1.0000)보시면 a와 b의 유사도는 마이너스가 나왔고, a와 c는 1이네요.
1이 나왔다는건, 두 벡터간에 이루는 각도가 0이라서 두 길이가 손실 없이 같은 방향으로 이어졌다는 의미겠군요.
마이너스가 나왔다는건 방향이 다르다는 겁니다. 만약 -1이라면 두 벡터는 같은 길을 가는방향만 반대로 가고 있다는 의미겠지요.
벡터의 유사도는 AI에서 아주 중요하게 쓰이는 걸로 알고 있습니다.
가령 NLP를 한다고 하면 단어를 벡터로 나타내야 하는데,
엄마랑 비슷한 단어를 알려달라 라고 했는데 뜬금없이 용가리가 나오면 안되겠죠.
그래서 엄마라는 단어의 벡터와 어머니 라는 단어의 벡터는 비슷하게 생겨야 합니다.
엄마 벡터와 어머니 벡터의 유사도가 1에 수렴해야 잘 만든 임베딩 모델이라고 설명할 수 있을 것 같습니다.
