Achievement Goals
- 자료구조가 무엇인지 설명할 수 있다.
- Stack, Queue, Tree, Graph 자료구조에 대해 이해할 수 있다.
- 알고리즘 문제에서 Stack, Queue 자료구조를 배열로 대체하여 흉내낼 수 있다.
- 각 자료구조의 개념과 구조를 파악하고 목적을 이해할 수 있다.
- 알고리즘 문제의 각 상황에 맞는 자료구조를 떠올릴 수 있다.
- 트리 및 그래프의 탐색 기법에 대해 이해할 수 있다.
- Binary Search Tree를 이해할 수 있다.
- BFS와 DFS의 개념을 이해하고 알고리즘 문제에서 사용할 수 있다.
- 자료구조를 활용하여 알고리즘 문제에 접근할 수 있다.
Stack
- 데이터를 순서대로 쌓는 자료구조
- 먼저 들어온 자료는 가장 나중에 나올 수 있다.
- ex)브라우저 뒤로가기,앞으로 가기
coplit 브라우저 뒤로 가기 앞으로 가기
function browserStack(actions, start) {
let prev=[]
let next=[]
let page=start
for(let i of actions){
if(i===-1&&prev.length!==0){
next.push(page)
page=prev.pop()
}else if(i===1&&next.length!==0){
prev.push(page)
page=next.pop()
}else{
prev.push(page)
next=[]
page=i
}
}return([prev,page,next])
}
Queue
- 데이터를 줄 세우는 자료구조
- 먼저 들어온 자료부터 처리
- ex)프린트 인쇄 작업 , Buffer
coplit 프린터
function queuePrinter(bufferSize, capacities, documents) {
let count=0
let queue=[]
let total = 0
for(let i=0;i<bufferSize;i++){
queue.push(0)
}
let curDocument=documents.shift()
queue.unshift(curDocument)
queue.pop()
total=curDocument
count++
while(total>0){
total-=queue.pop()
curDocument=documents.shift()
if(total+curDocument<=capacities){
queue.unshift(curDocument)
total+=curDocument
}else{
documents.unshift(curDocument)
queue.unshift(0)
}
count++
}
return count
}
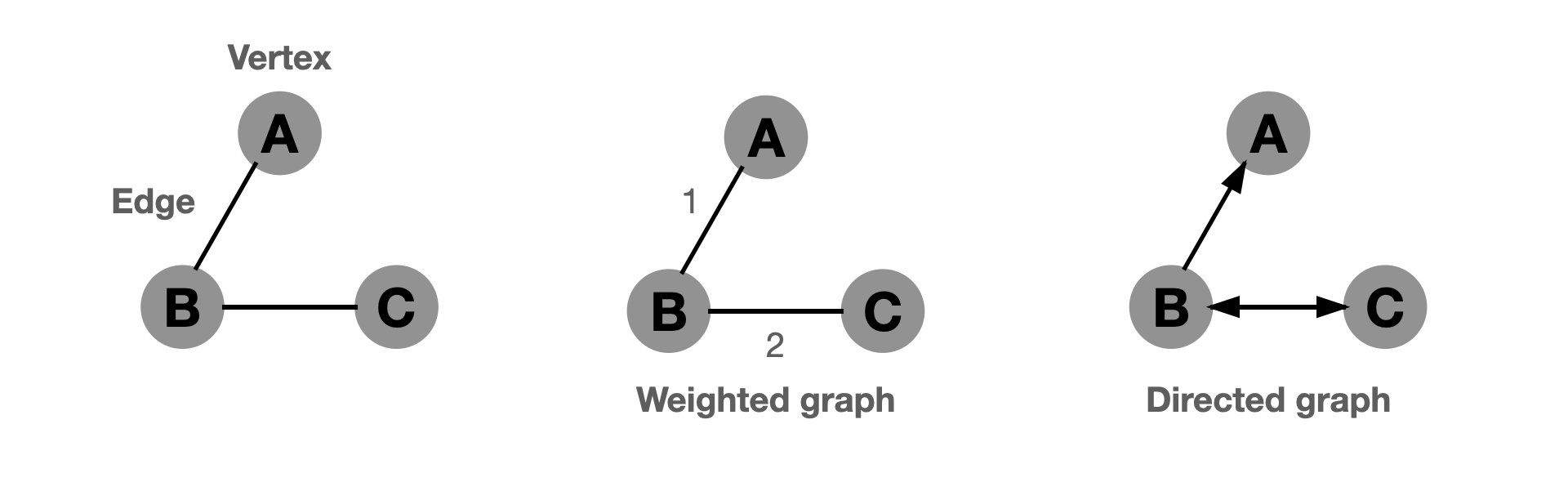
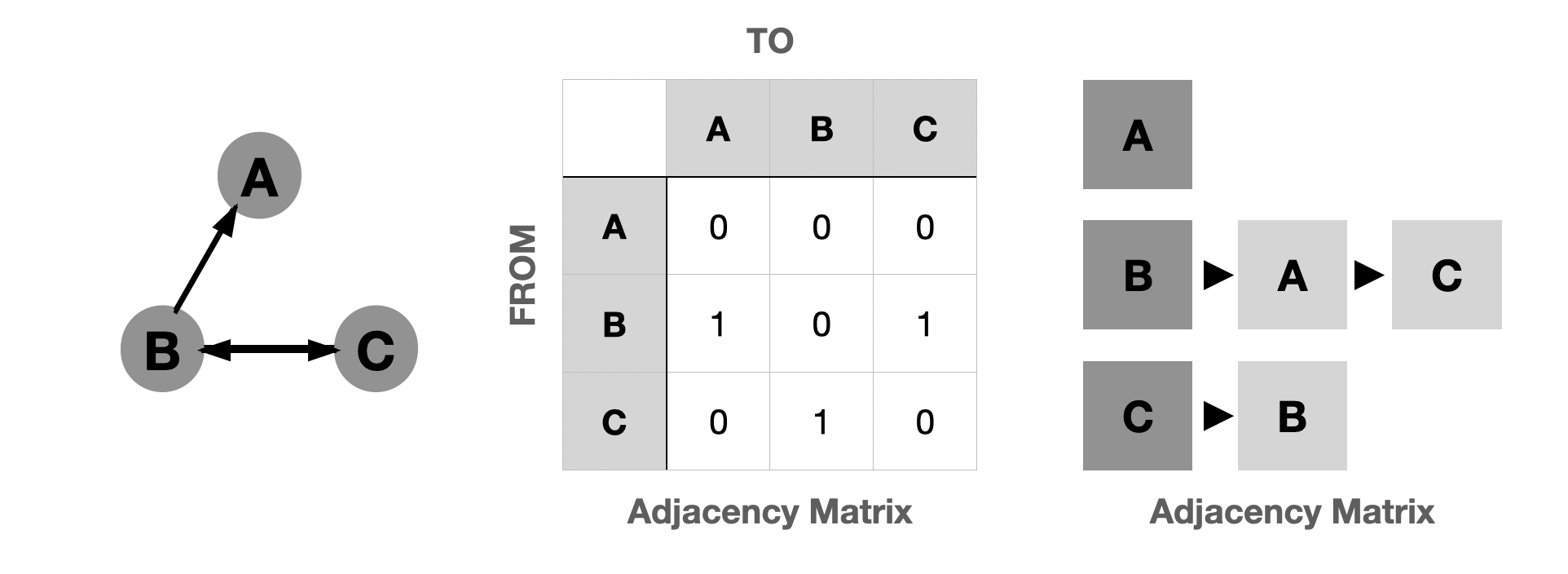
Graph
- 여러개의 점들이 서로 복잡하게 연결되어 있는 자료구조
- ex)포털 사이트 검색 엔진, SNS사람관걔, 네비게이션
Tree
- 단방향 그래프 구조로 뿌리로부터 가지가 사방으로 뻗은 형태
- ex)월드컵 토너먼트 대진표, 가계도 조직도



