logistic regression은 머신러닝 엔지니어 기술면접에서 자주 등장하는 질문이다. 비교적 간단하면서도 늘 머신러닝 교재의 앞쪽 챕터에 등장하는 알고리즘 때문이 아닐까?
그런데 기술면접에서 이 질문은 늘 나를 헷갈리게 한다.
내가 배운 Logistic Regression은 통계학에서의 일반선형회귀(Generalized Linear Model)의 하나의 특수한 형태였고 분포를 기반으로 하는 모델이다. 그래서 GLM에 관한 중요한 특징인 link function에 대해 대답하면 상대방은 고개를 갸웃하며 Gradient Decent는요? Sigmoid는요? 하고 물어보는 식이었다. 나는 재차 Regression을 추정하는 방법을 이야기하고 상대방은 weight는 어떻게 되나요? 라고 다시 묻는다.
나와 상대방은 전혀 접접이 없는 듯 하다!
정말로 나는 엉뚱한 대답을 한 것일까?
아마 통계학과를 졸업한 사람이라면 이런 일을 겪은 사람이 있을지도 모르겠다. 머신러닝의 세계와 통계학의 세계가 다른 것인가? 그리고 나도 머신러닝 교재를 읽을 때마다 이 부분에 대해서 명확하게 하지 못하고 넘어가고 있었다.
ChatGPT에 물어보니 뭔가 다른 점이 있는 것 같기도 하다. 많은 내용 중에서 이 부분이 눈에 들어왔다.
통계적인 방법의 Logistic Regression(MLE 추정)은 현상을 해석하는데 중점을 두고 있고 머신러닝 도메인에서의 Logistic Regression은 예측(이 경우에는 분류예측)에 더 적합하다는 것이다.
Applicability in Different Contexts:
MLE: Preferred in traditional statistical analysis and smaller datasets where the focus is on the interpretability of the model parameters and where computational resources are not a constraint.
SGD: More commonly used in machine learning, especially with large datasets or in situations requiring online learning, where new data comes in a stream, and the model needs to adapt continuously.
통계학에서의 Logistic Regression
앞에서 말했듯이 통계학에서의 Logistic Regression은 특수한 형태의 선형모델이다. 선형모델이라고 하면 일반적으로 아래 그림의 왼쪽과 같은 회기선을 그어야 겠지만 분류 모델의 경우에 아래 그림의 왼쪽 그림 처럼 그림을 그려버리면 어떤 예측은 0 이하가 되버리고 어떤 예측은 1 이상이 되어버린다. 그리고 가운데 위치한 예측들도 현실성이 떨어진다. 따라서 다른 방법이 필요하고 결과적으로 아래 그림의 오른쪽 처럼 되는 것이 Logistic Regression이다.
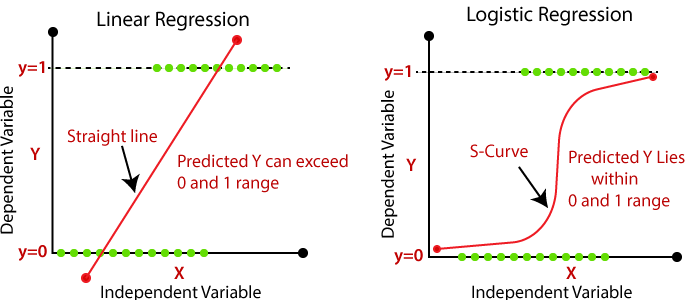
여기에는 link function이라는 개념이 매우 중요하다. 앞에서 Logistic Regression은 Generalized Linear Model이라는 언급을 했는데, 선형 모델에 대한 일반화를 시켜주었다는 뜻이다. 이 일반화 과정에 필요한 것이 link function이다.
먼저 Simple Linear Regression Form 이 이라는 걸 생각해보자. 위 그림의 왼쪽에 해당하는 단순 선형 관계이다. 그런데 단순 선형 모델에서 예측 target이 원래는 선형이었다면 이제는 예측 target을 0 과 1 사이에 놓이도록 odds(통계학에서 odds는 0과 1사이 어딘가에 놓인 어떤 비율 같은 개념으로 주로 사용 한다)로 변경하는 것이다. 이때 이 odds를 만드는 방식에 바로 log odds를 사용하는데 이 형태가 아래 수식에서 log를 포함한 좌변이다.
log odds라고 표현하기도 하고 logit link function 이라고 표현하기도 한다. 여기서 사용된 의 정의는 로써 0과 1을 시행의 실패 또는 성공(0 또는 1) 으로 분류했을 때 성공(1)이 될 수 있는 확률을 의미한다. 그러니깐 log odds라는 것은 을 의미하는 것이다. 이러한 형태의 regression 모델을 만드는 것이 전부이다.
우리가 익숙하게 보는 과 같은 형태가 있는데 이것은 결국 위 logistic regression을 깔끔하게 정리한 것에 지나지 않는다. ()
그리고 남은 과정은 결국 단순 선형 회기와 마찬가지로 coefficient를 추정하는 과정이 남는데, 데이터에 대한 분포의 가정이 정규 분포가 아닌 경우OLS로 추정할 수 없기 때문에 MLE로 추정을 하게 된다. 특히 binary classification의 경우 이 분포는 Bernoulli Distiribution으로써 likelihood 함수가 와 같이 정의 된다. MLE(maximum likelhook estimation) 에 대한 추정은 이번 글에서의 범위를 넘어서므로 이 추정이 때로는 미분을 사용한 closed form으로 풀릴 수 있으며 컴퓨터는 그 일을 하지 못하므로 몇 가지 알려진 방법을 사용해서 수치적으로 풀어낸다는 점으로 간략하게 언급하기로 한다.
머신러닝에서의 Logistic Regression
사실 아직 머신러닝에서의 Logistic Regression을 명확히 분리해서 생각하긴 어렵다. 하지만 Gradient Decent와 Weight의 변화는 이해가 되었다. 내 생각에는 머신러닝에서의 Logistic Regresion의 가장 큰 차이점은 역시 likelihood(머신러닝에서는 Cross Entrophy) 함수를 최대화 할 때 사용하는 방식에 있다. 그러니까 앞에서 통계적인 방법론으로는 미분을 한 후에 closed form으로 analytic solution(수학으로 해를 푸는 것의 다른 표현)을 구하는 것인데, 컴퓨터는 그런 일을 할 수 없으니 여러 데이터를 넣어보면서 coefficient(머신러닝에서는 weight) 들을 조정해나가면서 찾는 것이다. 그 과정에서 최소 지점을 찾기 위해 Gradient Decent를 사용한다(이제부터는 머신러닝 용어로만 사용하겠다). 그리고 logic function을 Sigmoid Function으로 부른다. Sigmoid Function의 장점은 미분의 형태가 아래와 같이 단순하다는 것이다.
위와 같은 형태를 이용하면 컴퓨터가 미분을 하지 않아도 이미 계산할 수 있는 형태의 form이 나오게 된다. 그리고 이 형태는 곧 delta룰과 비슷하게 target과 예측치의 차이에 learning rate을 곱하는 것과 유사한 형태가 나온다. 그리고 데이터가 들어오면 하나 하나씩 이 Gradient를 업데이트 해나가는 것이다. Bishop 책을 보면 이 과정이 좀 더 상세하게 설명되어있다.
최종 형태는 아래와 같다.
결국 이 에러의 크기를 최소화할 수 있는 Validation을 지속적으로 하게 되고 최적 weight를 찾는 것으로 마무리를 하게 될 것이다. 언뜻 보면 통계적인 방식과 무엇이 다른지 직관적으로 이해하기는 어렵다. 하지만 좀 더 공부를 해봐야 할 것 같다. 아직까지는 검색이나 책을 통해서 이해하는데 한계가 있었다. 좀 더 시간이 지나면 이해가 되면 좋겠다.
Reference
[1] An Introduction to Statistical Learning (T.Hastie 외)
[2] Pattern Recognition and Machine Learning (C.Bishop)
[3] Speech and Language Processing. Daniel Jurafsky & James H. Martin. Copyright © 2023. All
rights reserved. Draft of February 3, 2024. https://web.stanford.edu/~jurafsky/slp3/5.pdf
