기존 공부했던 자료구조인 순차적 자료구조(배열, 연결리스트) 외에 다른 자료구조인 트리 구조에 대해 공부해봤다.
트리구조
부모노드와 자식노드들이 하나씩 연결되어 있는 구조를 트리 구조라고 한다.
연결리스트는 부모 노드와 자식 노드가 하나씩만 존재하는 일종의 트리 구조이다.
이진트리는 부모 노드가 자식을 최대 2개 까지 가질 수 있는 트리를 이진 트리라고 부르며 가장 흔하게 사용된다.
단어 정리
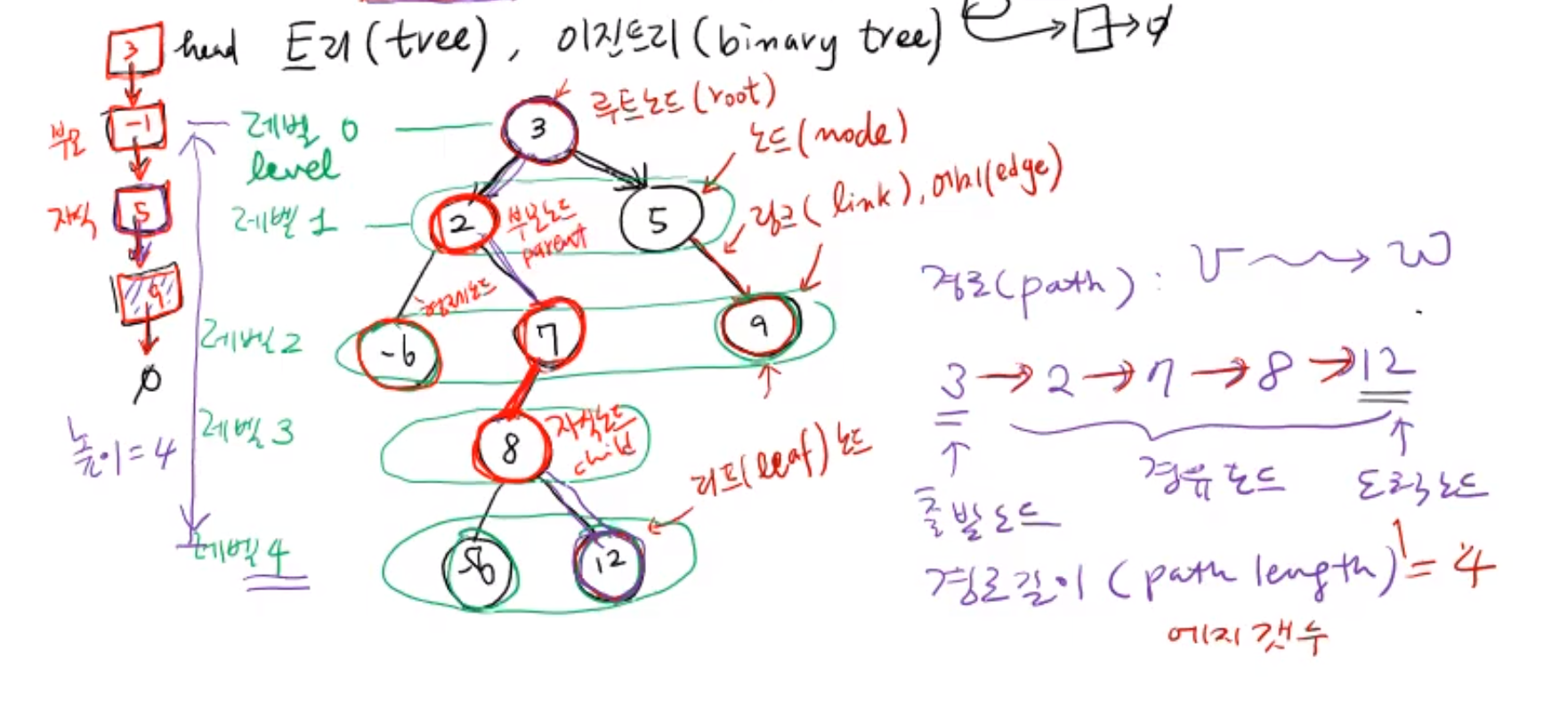
노드와 관련된 단어
부모 노드 : 어떤 노드의 바로 위에 있는 노드이며 루트 노드를 제외한 모든 노드는 부모 노드를 갖는다.
자식 노드 : 어떤 노드의 바로 아래에 있는 노드를 자식 노드라고 한다. 이진 트리에서 각 노드는 최대 두 개의 자식 노드를 가질 수 있음
형제 노드 : 같은 부모 노드를 가진 노드를 형제 노드라고 한다. 부모 노드를 기준으로 서로 다른 자식을 가진 노드들이 형제 관계에 있다.
루트 노드 : 이진 트리 구조에서 최상위에 있는 노드를 가리킨다. 트리의 시작점이며 모든 다른 노드들은 루트 노드에서 어떤 경로든 연결되어 있다. 루트 노드는 부몬 노드를 가지지 않는다.
리프 노드 : 이진 트리 구조에서 자식 노드를 가지지 않는 노드를 가리킨다.
경로와 관련된 단어
링크 혹은 엣지 : 부모노드와 자식 노드를 연결한 선이나 화살표
경로 : 두 노드간 이어진 링크들의 순차적 모습을 나타낸다. 루트 노드에서 시작해 어떤 리프노드로 가는 경우는 다운 경로, 반대로 리프 노드에서 루트 노드를 향해 가는 경우는 업 경로라고 한다.
경로의 길이 : 해당 경로를 이루는 링크의 수
깊이와 관련된 단어
- 레벨 : 트리의 각 층을 레벨이라고 한다. 루트노드는 레벨1
- 높이 : 트리의 높이는 가장 깊은 레벨의 높이를 나타낸다.
이진 트리의 다양한 구현법
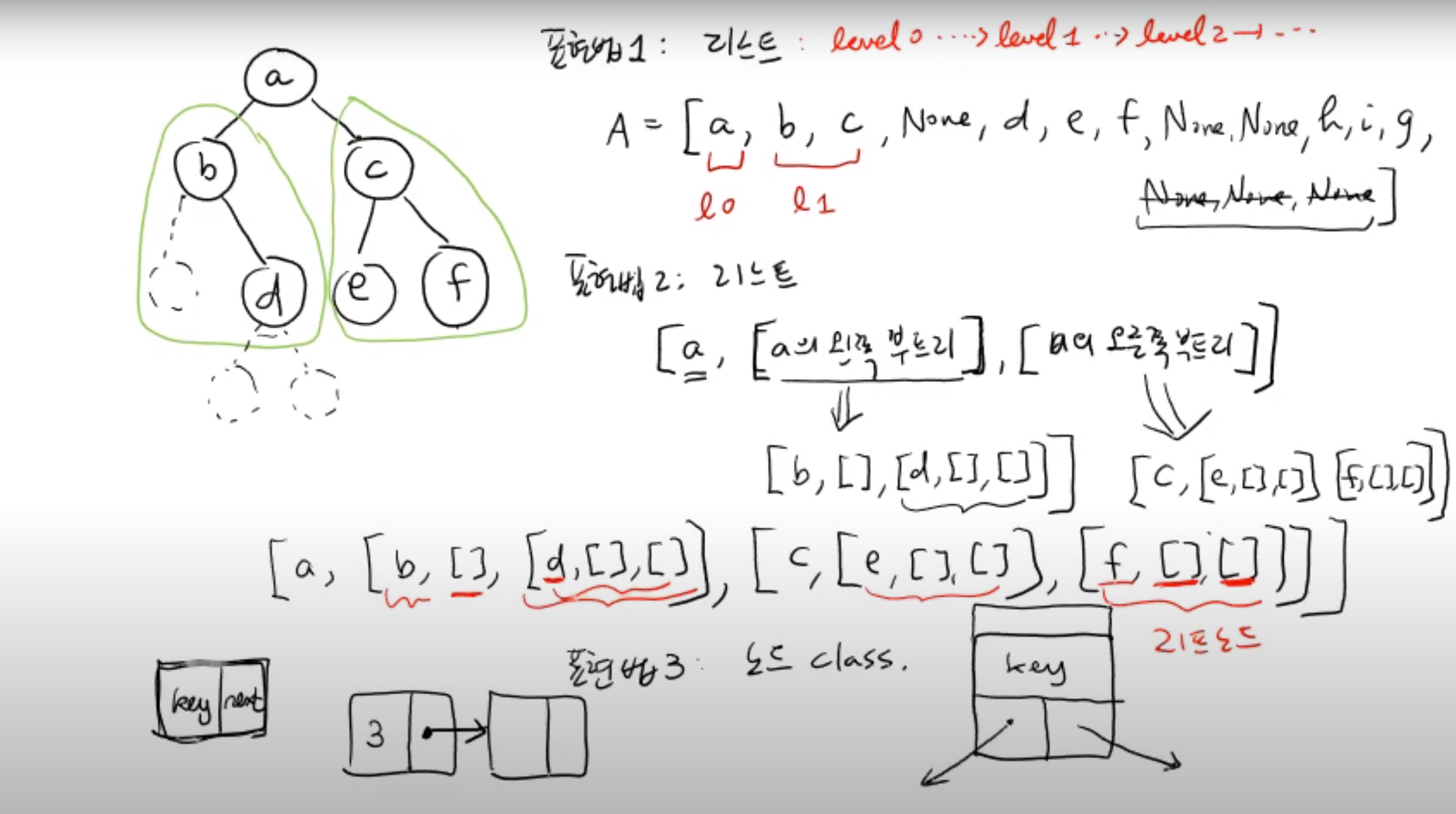
표현법 1 : 리스트로 표현하기
루트 노드부터 왼쪽 자식 노드, 오른쪽 자식 노드 순으로 배열에 담는다.
루트 노드의 자식 노드를 모두 담았으면 자식 노드가 담긴 순서대로 부모 노드가 되어 다시 왼쪽 자식 노드 , 오른쪽 자식 노드 순으로 담는다.
이 때 자식 노드가 없는 경우엔 None 으로 하여 담는다.
표현법 2 : 재귀적으로 표현하기
배열에 3가지 원소가 들어가는데
첫 번째 원소는 노드값 , 두 번째 원소는 첫 번째 원소의 좌측 부트리, 세 번째 원소는 첫 번쨰 원소의 우측 부트리가 들어가게 된다.
이 때 특정 부트리의 값이 존재 하지 않는다면 빈 리스트로 표현한다.
표현법 3: 노드 class 를 이용하여 직접 구현하기
class Node:
def __init__(key,parent,left,right):
self.key = key
self.parent = parent
self.left = left
self.right = right힙 (heap)
정의
힙 성질을 만족하는 이진 트리

기본적으로 배열에는 모든 노드들이 들어가며 배열의 길이는 (루트 노드는 하나이기 때문)이다.
배열에 노드를 담는 순서는 부모 노드와 왼쪽 자식 노드, 오른쪽 자식 노드가 들어가며 자식 노드가 없는 경우엔 값을 담는다.
만약 배열의 k 번째 노드의 왼쪽 자식 노드가 알고 싶을 때는 , 오른쪽 자식 노드가 알고 싶을 때는 를 하면 된다.
왜 ?
깊이가 한 단계씩 내려갈 때 마다 원소의 개수는 배씩 증가하기 때문에 번째 노드의 다음 레벨에서의 위치는
배열을 적어 나갈 때 [부모 노드 , 왼쪽 자식 노드 , 오른쪽 자식 노드] 순으로 적어나간다고 하였기 때문에 이후 왼쪽 자식 노드일 땐 + 1 , 오른쪽 자식 노드일 땐 + 2 를 해준다.
반대로 k 번째 노드의 부모 노드를 알고 싶다면 자식 노드를 구했던 식의 연산으로 을 통해 구할 수 있다.
장점
인덱스를 통해서 배열을 조회할 수 있기 때문에 만에 자식 노드를 구하고, 부모 노드를 구할 수 있다.
단점
자식 노드가 없는 경우엔 값으로 저장하기 때문에 불필요한 메모리 소모가 존재한다.
힙성질
힙은 힙성질을 만족하는 이진 트리라고 하였다.
힙성질은 두 가지가 존재한다.
- 모양 성질
- 모양 성질은 위처럼 배열에서 레벨 순으로 패턴을 가지고 적은 형태를 말한다.
- 힙 성질
- 모든 부모 노드에 key 값은 자식 노드의 key 값보다 작지 않다.
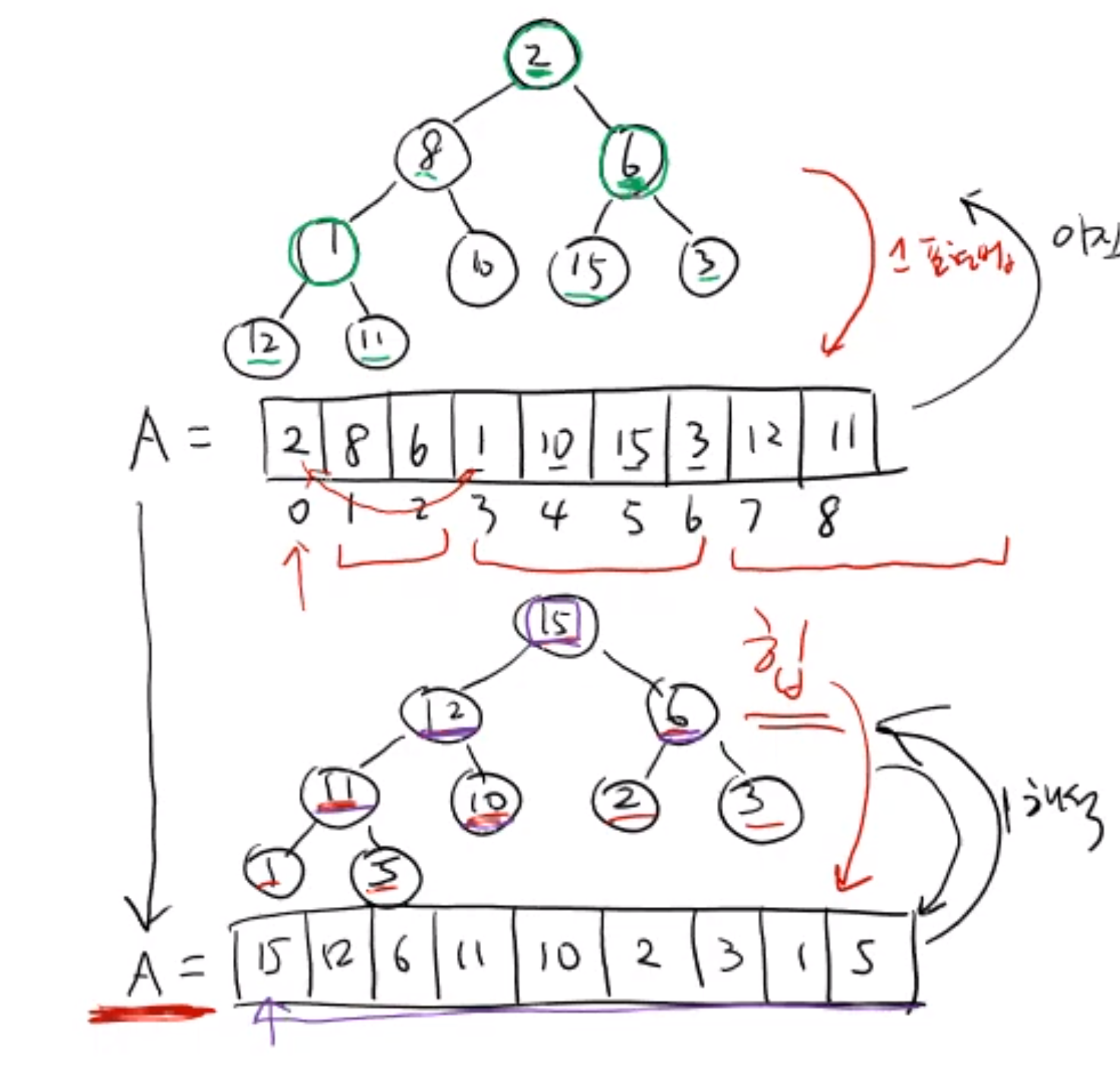
예를 들어 첫 번째 이진 트리는 모양 성질은 만족하지만 힙 성질을 만족하지 못하니 힙 성질은 아니다.
두 번째 이진 트리는 모양 성질과 힙 성질을 모두 알고 있기 때문에 힙이라고 볼 수 있다.
힙을 사용하게 될 때의 가장 큰 특징은 루트 노드가 가장 큰 값으로 이뤄져있기 때문에 트리의 최대 값을 0번째 인덱스만 조회하면 되기 때문에 상수 시간 내에 조회 할 수 있다.
