재귀함수는 무엇이고 장점과 단점이 무엇일까 ?

ChoiYongHyeun·2023년 11월 13일

알고리즘 이론

목록 보기

1/9

스택 프레임

메모리의 스택 (stack) 영역은 함수의 호출과 관계되는 지역변수와 매개변수가 저장되는 영역이다.

스택 영역은 함수의 호출과 함께 할당되며, 함수의 호출이 완료되면 소멸한다.

def my_function(parameter):  # 매개변수(parameter)
    my_variable = 10  # 지역 변수
    
    print("매개변수(parameter):", parameter)
    print("지역 변수(my_variable):", my_variable)

argument = 5  # 전역 범위에서 정의된 변수 

my_function(argument)  # my_function 호출, argument를 parameter로 전달

# my_function이 실행을 마치고 돌아온 후, 여기에서는 my_variable과 parameter는 더는 유효하지 않음
# 따라서, 이 시점에서 해당 변수들은 메모리에서 해제됨

함수가 호출되면 스택에서는 함수의 매개변수 , 호출이 끝난 뒤 돌아갈 반환 주소값, 함수에서 선언된 지역 변수 등이 저장된다.

반환 주소 값 : 함수 호출 이전에 실행되던 코드의 위치

이렇게 스택 영역에 차례대로 저장되는 함수의 호출 정보를 스택프레임 (stack frame) 이라고 한다.

이러한 스택 프레임 덕분에 함수의 호출이 모두 끝난 뒤에, 해당 함수가 호출되기 이전 상태로 되돌아 갈 수 있다.

스택 프레임의 동작 방식

main() -> func1() -> func2() 로 연결되는 함수들을 통해 스택 프레임을 이해해보자

def func2():
    pass  # 아무 동작도 하지 않는 func2 함수

def func1():
    func2()  # func2 호출

def main():
    func1()  # func1 호출
    return 0

# main 함수 호출
print(main())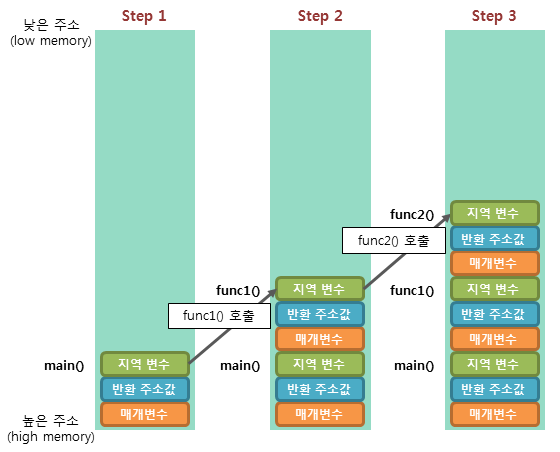

step1 : 프로그램이 실행되면 가장 먼저 main 함수가 호출되어 main 함수의 스택 프레임이 스택에 저장된다.
step2 : func1() 함수를 호출하면 해당 함수의 매개 변수, 반환 주소값, 지역 변수 등의 스택 프레임이 스택에 저장된다.
step3 : func2() 함수를 호출하면 해당 함수의 매개 변수, 반환 주소값, 지역 변수 등의 스택 프레임이 스택에 저장된다.

호출이 끝난 이후

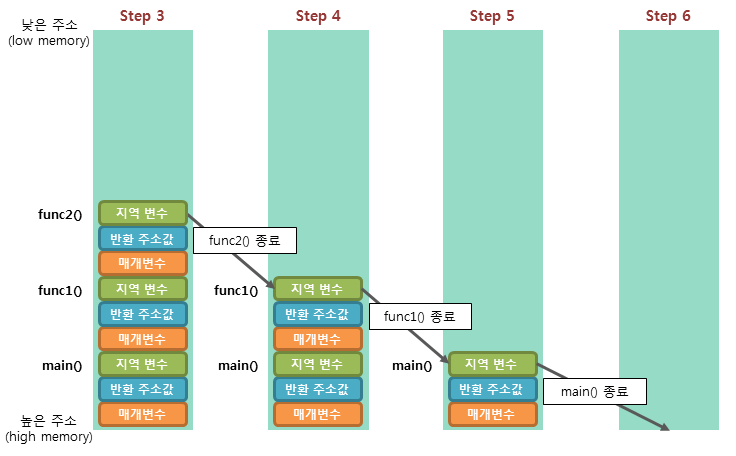
step4: func2() 함수의 모든 작업이 완료되면 func2() 함수의 스택 프레임이 스택에서 제거된다.
step5 : func1() 함수의 모든 작업이 완료되면 func1() 함수의 스택 프레임이 스택에서 제거된다.
step6 : main() 함수의 모든 작업이 완료되면, main() 함수의 스택 프레임이 스택에서 제거된다.
step7: main() 함수의 반환 주소값인 함수가 호출되기 이전의 위치로 돌아감

자료구조 중 하나인 stack 을 통해 동작한다. stack 은 후입선출 (Last-in First Out) 방식으로 동작한다.

스택 오버플로우 (stack overflow)

개발자 커뮤니티이름으로 유명한 스택 오버플로우는 해당 현상의 이름을 딴 것으로

함수의 재귀 호출이 무한히 반복되면 해당 프로그램은 스택 오버플로우에 의해 종료된다.

재귀함수 중 가장 대표적인 팩토리얼 (factorial) 을 통해 알아보자

def factorial(n):

  if n <= 1:
    return 1

  return n * factorial(n-1)

print(factorial(5))

해당 재귀 함수를 실행하게 되면

5 x factorial(4)
5 x 4 x factorial(3)
5 x 4 x 3 x factorial(2)
5 x 4 x 3 x 2 x factorial(1)
5 x 4 x 3 x 2 x 1 종료

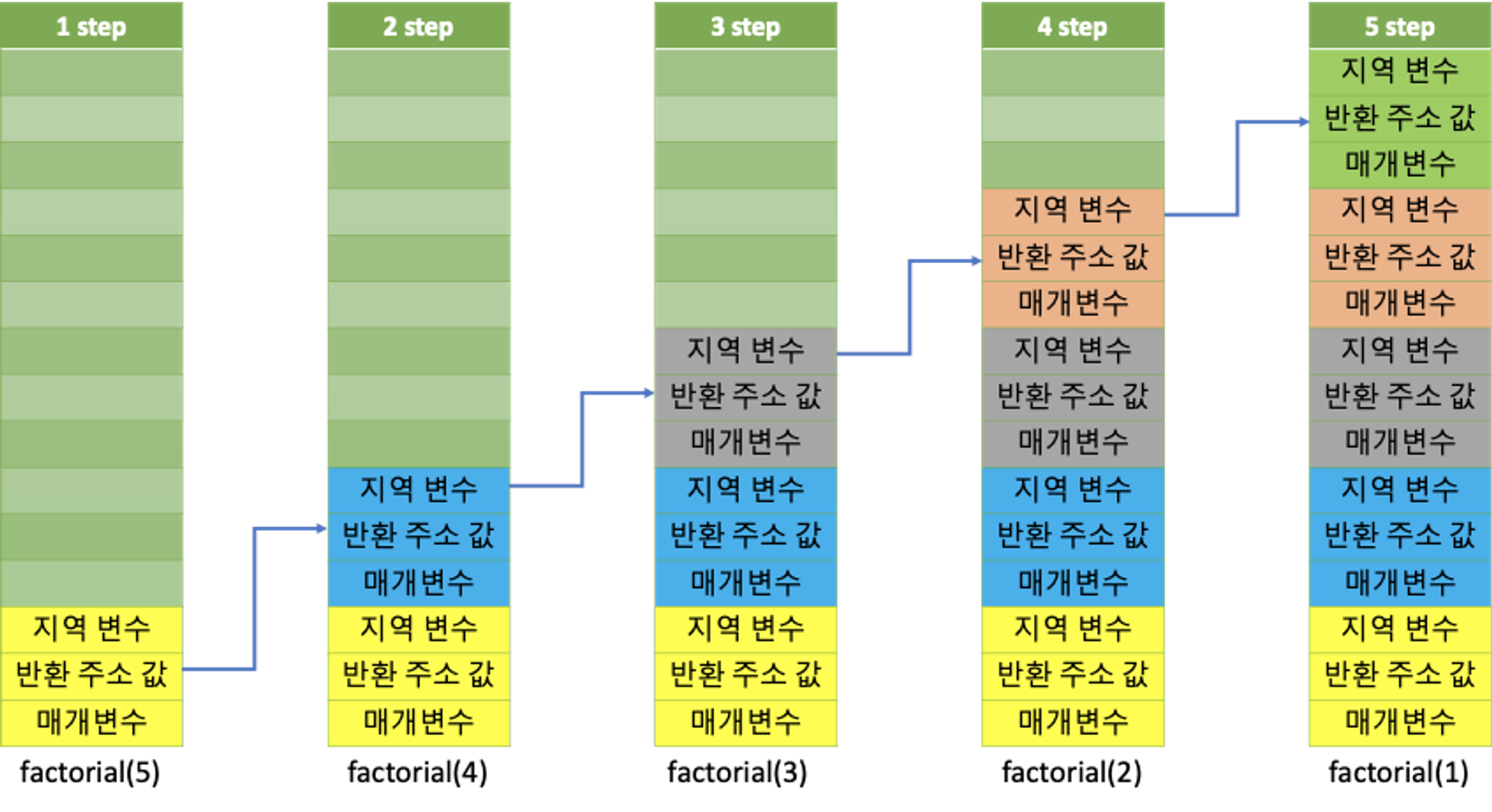
n 값이 1 이하가 될 때 까지 지속적으로 콜스택 에 함수들의 지역변수, 매개변수, 반환 주소 값 등이 저장 되면서 반복적으로 factorial(n)이 호출되다가 n 값이 1이 되는 순간 콜스택 에서 함수 호출이 종료되면서 차례대로 콜스택에서 pop 해가며 수행되며 사라지게 될 것이다.

이 때 만약 n 이 1이하일 때 1 을 return 하라는 구문을 제거하고 사용하게 되면 다음과 같은 오류가 발생한다.

def factorial(n):
  # if n <= 1:
  #   return 1
  return n * factorial(n-1)

print(factorial(5))

RecursionError: maximum recursion depth exceeded

n이 1일경우 멈추지 않으니 -1 , -2 , -3 .... $-\infty$ 까지 실행이 계속 될 것이다.

이 때 컴퓨터의 메모리는 한계가 있기 때문에 콜스택 의 용량보다 많은 정보들이 저장되는 순간

스택 오버플로우 가 발생하게 된다.

기본적인 콜스택의 용량은 언어에 따라 할당된 크기가 존재하며 일반적으로 몇 메가 바이트 정도의 크기이다. 파이썬에서는 1 ~ 3MB 사이다.

import sys

# 현재 재귀 한도 확인
print(sys.getrecursionlimit())  # 기본값

# 재귀 한도를 늘릴 값 설정 (예: 5000)
sys.setrecursionlimit(5000)

다음과 같은 방식으로 메모리를 늘릴 수 있지만 재귀 하수의 호출 한도를 증가시키면 메모리 사용량도 증가하므로 적절한 한도로 설정하는 것이 중요하며, 재귀 호출이 길어진다면, 코드를 반복문 등 다른 방법으로 변경하는 것이 더 바람직 할 수 있다.

재귀함수의 장단점

장점

변수를 여럿 만들 필요가 없다. 현재 상태를 저장해야 할 경우 임시 변수를 만들기보다 함수를 재귀적으로 호출하면서 변경된 상태를 전달함으로서 변수의 수를 줄일 수 있다.
반복문을 사용하지 않아도 되기 때문에 코드가 간결해진다.

단점

지속적으로 함수를 호출하게 되면서 지역변수, 매개변수, 반환주소값 모두 콜스택 에 저장해ㅑ 한다. 이러한 과정은 임시 변수를 사용하는 반복문에 비해서 메모리를 더 많이 사용하게 되고 속도 저하로 이어진다.
함수 호출 -> 복귀를 위한 컨텍스트 스위칭에 비용이 발생하게 된다.

컨텍스트 스위칭

함수 호출 및 복귀 과정에서의 문맥 스위칭은 현재 실행 중인 함수의 상태를 저장하고 다른 함수로 이동하는 과정을 말합니다. 이것은 컴퓨터가 코드를 실행하는 동안 함수 간의 전환과 실행 위치를 추적하는 데 사용됩니다.

이러한 문맥 스위칭은 함수가 호출되면 호출된 함수에 필요한 정보를 스택에 저장하고, 호출된 함수가 종료되면 그 함수의 정보를 스택에서 제거하여 이전 함수로 돌아가는 과정을 의미합니다. 이때, 현재 실행 위치, 지역 변수, 매개변수, 반환 주소 등이 스택 프레임에 저장되어 컨텍스트 스위칭이 이루어집니다.

이 작업은 프로그램의 흐름을 유지하고 함수 호출 및 복귀를 관리하는 데 필요하지만, 이 과정에서 오버헤드가 발생할 수 있습니다. 특히, 많은 함수 호출이 발생할 때 이러한 스위칭은 시스템 자원을 사용하며, 이로 인해 성능 저하가 발생할 수 있습니다.

따라서, 재귀 함수 또는 많은 수의 중첩된 함수 호출을 사용하는 경우에는 이러한 문맥 스위칭에 따른 오버헤드를 고려해야 합니다. 종종 반복문이나 다른 방식으로 문제를 해결하는 것이 더 효율적일 수 있습니다.

그니까 재귀 함수는 코드가 간결해지는 장점이 있지만 많은 메모리 소모와 그로 인한 속도 저하 라는 치명적인 단점이 존재한다.