자료구조 힙 (heap) - insert와 delete_max 연산

이전 포스트에서 이진 트리를 힙성질 을 만족하도록 만드는 makeheap 함수를 이용해서 정렬하였다고 해보자

이 후 새로운 값이 들어왔을 때 여전히 힙성질을 만족하도록 값을 배열안에 새로운 값을 추가하는 insert 와 가장 높은 값을 제거하는 delete_max 함수를 이해해보자

insert 와 heapify_up

이론

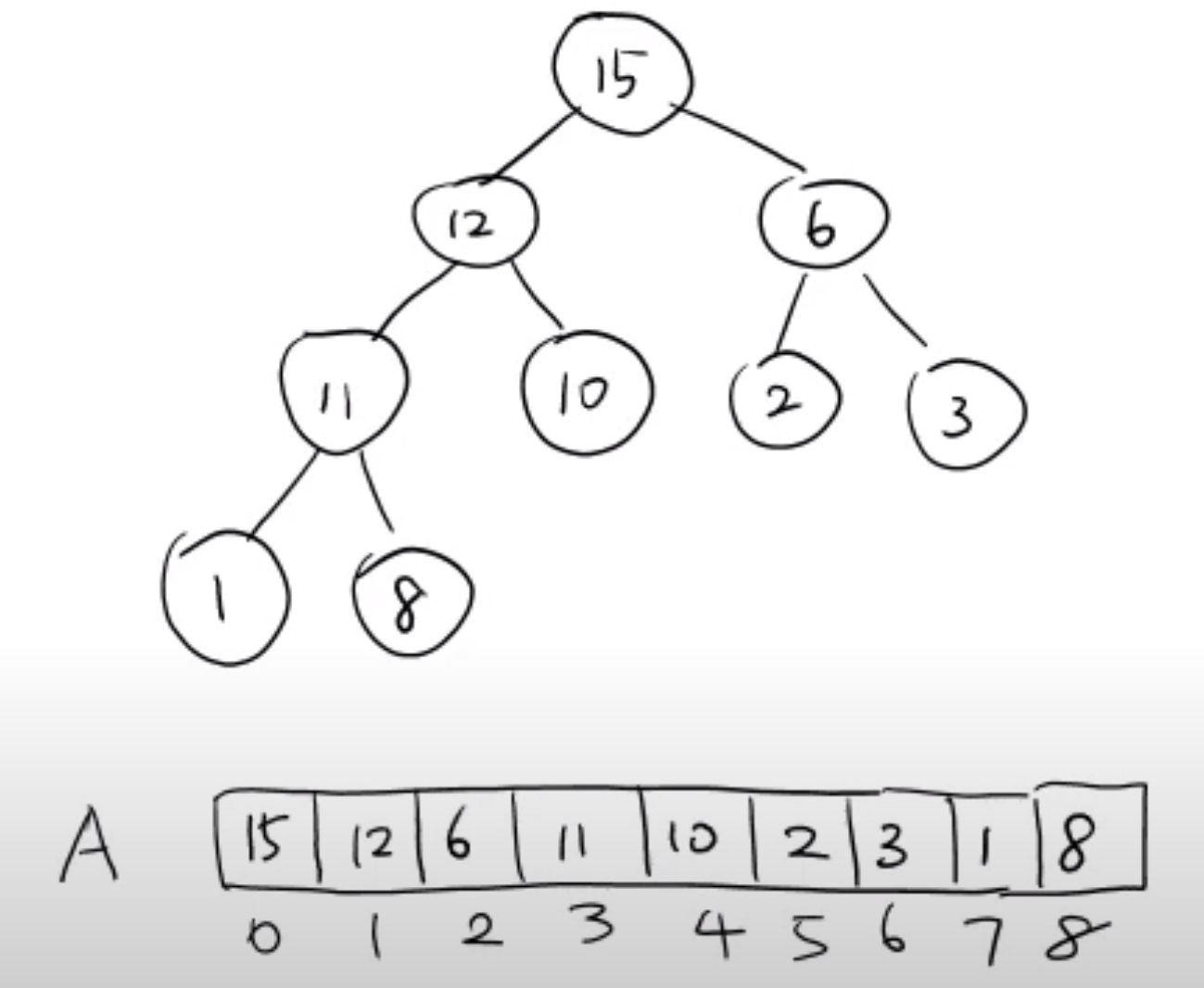
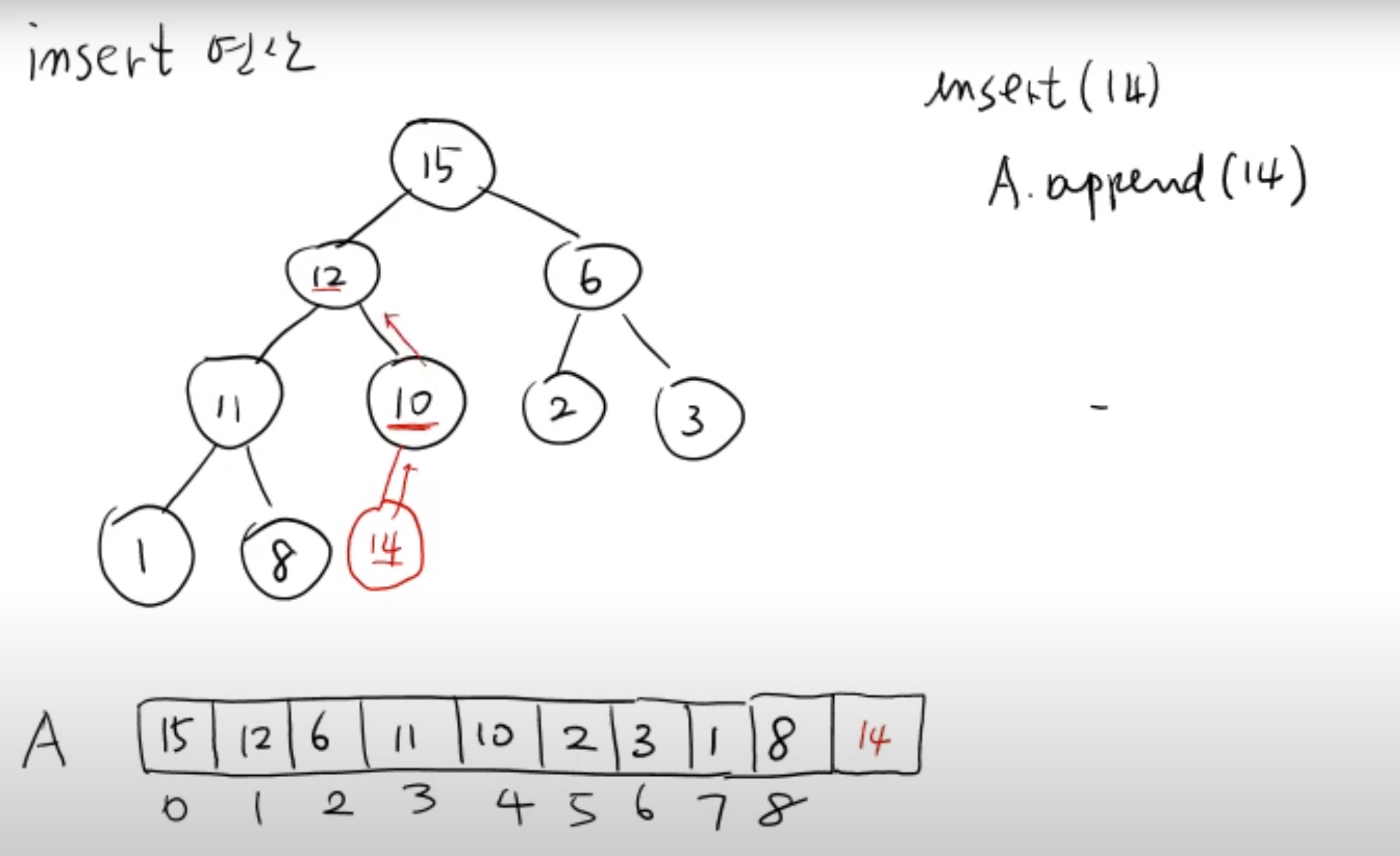
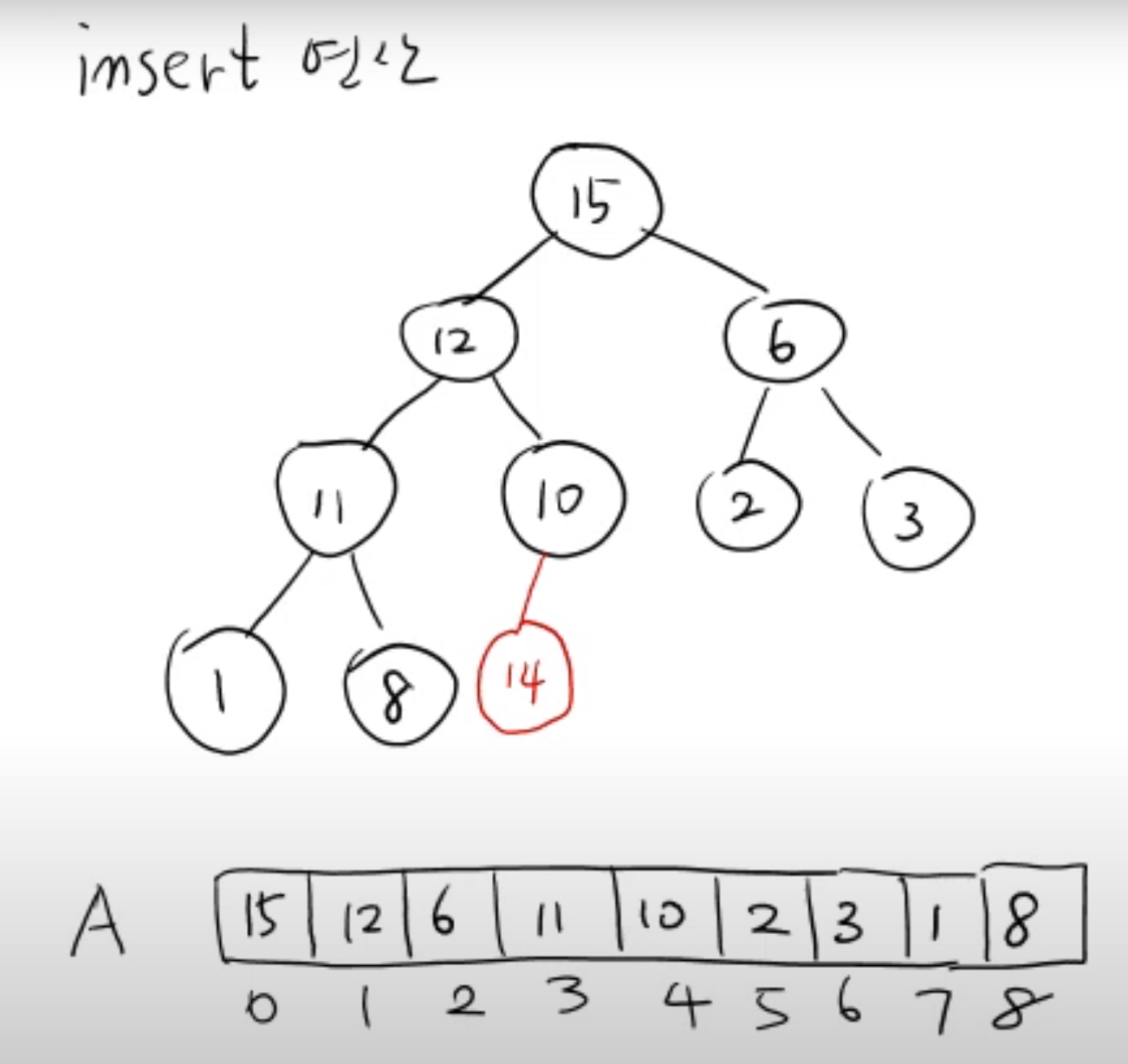
힙성질 을 만족하는 이진 트리에서 14 라는 값을 배열에 추가하였다고 하면 가장 마지막 leaf node 자리에 14 라는 값을 넣기 때문에 그저 배열에 append 하는 것과 같다.

값을 append 한 이후에도 이진 트리가 힙성질 을 만족하는가를 봐야 하며 만약 만족하지 않는다면 힙성질 을 만족하도록 다시 재배치 해야 한다.

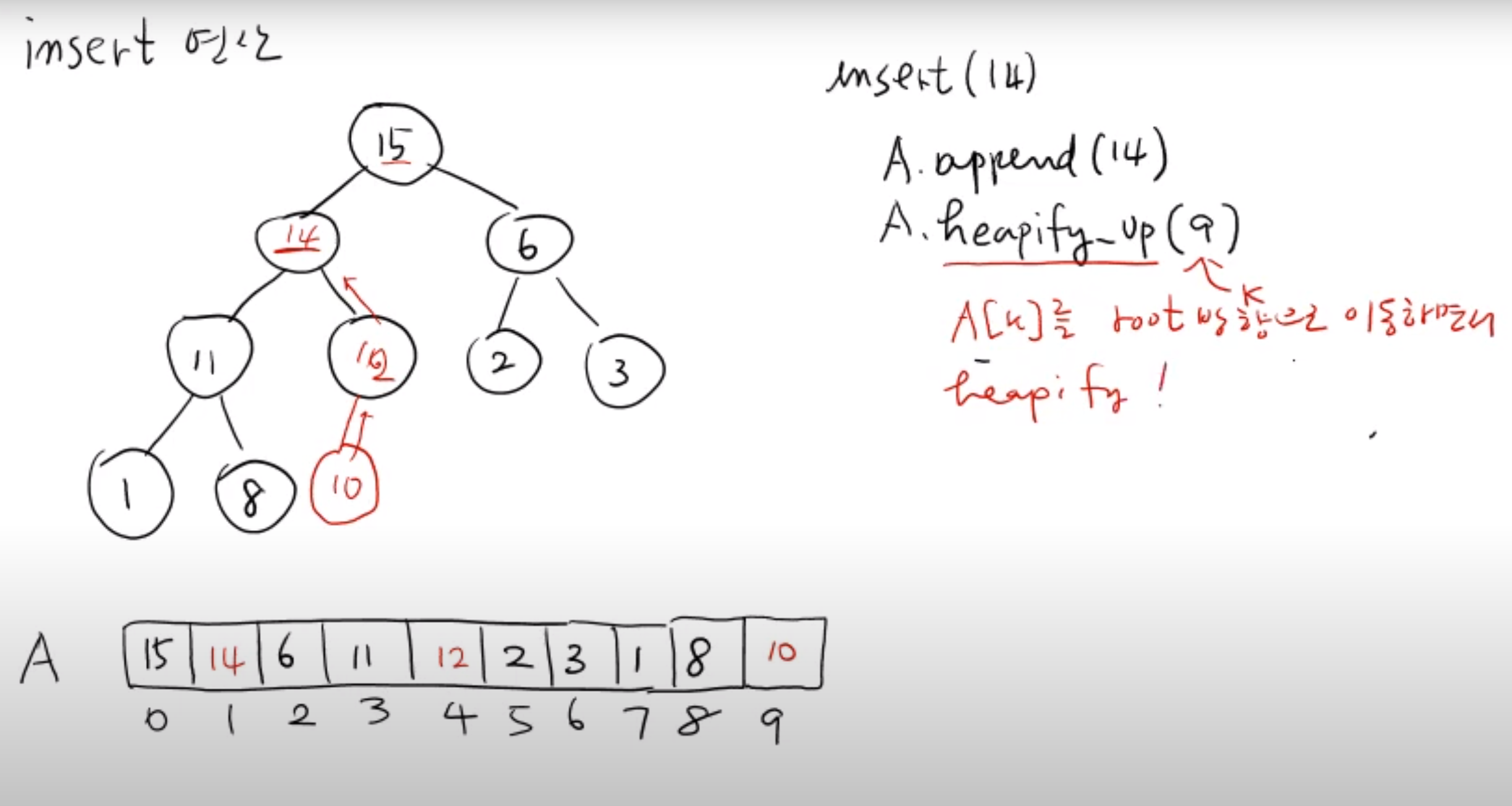
마지막 인덱스에 14 라는 값이 들어왔다면 여전히 힙성질 을 만족하도록 해야 하기 때문에 부모 노드들과 비교하며 root node 방향으로 힙성질 을 만족하도록 값을 변경해줘야 한다.

이 전에 makeheap 할 때는 leaf node 방향으로 부모노드와 자식노드 를 바꿔 나갔다면 heapfi_up의 경우에는 새로운 값이 leaf node로 배치되기 때문에 leaf node 에서 root node 방향으로 값을 변경해나가야 한다.

즉 새로운 값이 k 번째 index 에 추가되었다면 k 번째 index 부터 root node (0번째 인덱스) 방향으로 부모노드 와 비교해나가면서 힙성질 을 만족하도록 비교하고 변경해나가야 한다.

코드

class Heap:
  def __init__(self , L = []):
    self.A = L
    self.length = len(self.A)
    self.make_heap()

  def __str__(self):
    return str(self.A)
    
    ...
    
  def heapify_up(self):
    k = self.length - 1 # insert 된 값의 인덱스 
    # 배열의 마지막이기 때문에 insert 된 값의 인덱스는 len - 1 

    while k > 0 and self.A[(k-1) // 2] < self.A[k]: 
      '''
      반복문은 root node가 아니면서 자식 노드가 부모 노드보다 클 때 까지 반복 
      '''
      self.A[k] , self.A[(k-1) // 2] = self.A[(k-1) // 2]  , self.A[k]
      # while 문이 작동 되었다는 것은 insert 된 값이 부모노드보다 값이 크단 것이니
      # 부모노드와 자식 노드의 값을 변경 
      k = (k-1) // 2  # 자리가 바뀐 후 그 위 부모노드와의 값을 비교 

  def insert(self,value):
    self.A.append(value)
    self.length += 1
    self.heapify_up()

heapify_up 의 while 문을 살펴보면 부모노드 가 아니면서 insert 된 값 이 부모노드 보다 값이 클 때 반복적으로 수행된다.

부모노드 보다 insert 된 값 이 클 경우 부모노드 와 자식노드 의 자리를 바꾼 후 값이 바뀐 이후의 위치 에서 값이 바뀐 위치에서의 부모노드와 비교를 반복적으로 수행해나간다.

부모노드와 자식노드의 자리가 바뀌었을 때 바뀐 자식 노드는 힙성질을 만족하는가 ?

만족한다. 그 이유는 오른쪽 자식노드가 부모노드보다 값이 클 경우 오른쪽 자식 노드는 자동으로 왼쪽 자식 노드보다는 값이 클 수 밖에 없다. (이미 힙성질을 만족하도록 값이 있기 때문에)

변수 스왑

self.A[k] , self.A[(k-1) // 2] = self.A[(k-1) // 2] , self.A[k] 와 같이 한 줄로 배열의 값을 변경하는 것을 변수 스왑 이라고 한다.

다음처럼 한 줄로 값을 스왑 할 경우 임시 변수로 지정한 후 변경해줄 필요 없기 때문의 코드의 간결성이 더 좋아진다.

heapify_up 의 시간 복잡도

배열에서 인덱스로 값을 조회하거나 비교하는 것은 모두 $O(1)$ 만에 해결이 가능하고 최악의 경우는 root node 까지 올라가면서 값을 변경해야 하기 때문에 시간 복잡도는 이진 트리의 높이인 $h$ 만큼 걸린다.

이진 트리의 높이인 $h$ 는 아무리 커봐야 $log_2^n$ 이기 때문에 heapfiy_up 의 시간 복잡도는 $log_2^n$ 이다.

insert 또한 heapify_up 의 시간복잡도와 같다.

새로운 값이 들어왔을 때 모든 값을 meakheap 을 이용해서 정렬 할 필요 없이 새로 들어온 값에 대해서만 정렬해주면 되기 때문에 효율적이다.

find_max 와 delete_max

이론

힙성질을 만족하는 이진트리 의 대표적인 특징은 가장 높은 값은 root node 에 존재한다는 것이다.

find_max 는 root node 에 들어가있는 값을 return 하면 된다.

delete_max 는 root node 의 값을 leaf node 로 변경한 후 변경된 root node 부터 heapify_down 을 시행하면 된다.

class Heap:
  def __init__(self , L = []):
    self.A = L
    self.length = len(self.A)
    self.make_heap()

  def __str__(self):
    return str(self.A)
  
  def heapify_down(self,k):
    n = self.length
    '''
    n = 힙의 전체 노드수 
    A[k] 를 힙 성질을 만족하는 위치로 내려가면서 재배치
    '''
    
    while 2 * k + 1 < n:
      L,R = 2 * k + 1 , 2 * k + 2
      if self.A[L] > self.A[k]:
        m = L 
      else:
        m = k 
      
      if R < n and self.A[R] > self.A[m]:
        m = R 

      if m != k:
        self.A[k] , self.A[m] = self.A[m] , self.A[k]
        k = m 

      else:
        break
        
        ...
   def find_max(self):
    if self.length == 0:
      return None
    else:
      return self.A[0]
  
  def delete_max(self):
    if self.length == 0:
      return None
    else:
      self.A[0] = self.A.pop() # 마지막 leaf node를 root node 로 보냄
      self.length -= 1  
      self.heapify_down(0) # root node 부터 heapfipy_down 시행 

print('==' * 20)
print('MaxHeap')
arr = [2,6,5,1,3,0,7]
print('정렬 안된 이진 트리 : ', arr)
a = MaxHeap(L = arr)
print('현재 힙 성질을 만족하는 이진 트리 : ',a.A)
a.insert(7)
print('7 insert 이후 이진 트리 :', a.A)
print('find_max : ',a.find_max())
a.delete_max()
print('delete max 이후 값 : ',a.A)

========================================
MaxHeap
정렬 안된 이진 트리 :  [2, 6, 5, 1, 3, 0, 7]
현재 힙 성질을 만족하는 이진 트리 :  [7, 6, 5, 1, 3, 0, 2]
7 insert 이후 이진 트리 : [7, 7, 5, 6, 3, 0, 2, 1]
find_max :  7
delete max 이후 값 :  [7, 6, 5, 1, 3, 0, 2]

시간 복잡도

find_max 의 시간 복잡도는 $O(1)$
delete_max 의 시간 복잡도는 heapify_down 의 시간 복잡도는 $O(log_2^n)$ 만큼 걸린다.

전체 코드

class MaxHeap:
  def __init__(self , L = []):
    self.A = L
    self.length = len(self.A)
    self.make_heap()

  def __str__(self):
    return str(self.A)
  
  def heapify_down(self,k):
    n = self.length
    '''
    n = 힙의 전체 노드수 
    A[k] 를 힙 성질을 만족하는 위치로 내려가면서 재배치
    '''
    
    while 2 * k + 1 < n:
      L,R = 2 * k + 1 , 2 * k + 2
      if self.A[L] > self.A[k]:
        m = L 
      else:
        m = k 
      
      if R < n and self.A[R] > self.A[m]:
        m = R 

      if m != k:
        self.A[k] , self.A[m] = self.A[m] , self.A[k]
        k = m 

      else:
        break
  
  def make_heap(self):
    n = self.length
    for k in range(n-1 , -1, -1):
      self.heapify_down(k)

  def heapify_up(self):
    k = self.length - 1 # insert 된 값의 인덱스 
    # 배열의 마지막이기 때문에 insert 된 값의 인덱스는 len - 1 

    while k > 0 and self.A[(k-1) // 2] < self.A[k]: 
      '''
      반복문은 root node가 아니면서 자식 노드가 부모 노드보다 클 때 까지 반복 
      '''
      self.A[k] , self.A[(k-1) // 2] = self.A[(k-1) // 2]  , self.A[k]
      # while 문이 작동 되었다는 것은 insert 된 값이 부모노드보다 값이 크단 것이니
      # 부모노드와 자식 노드의 값을 변경 
      k = (k-1) // 2  # 자리가 바뀐 후 그 위 부모노드와의 값을 비교 

  def insert(self,value):
    self.A.append(value)
    self.length += 1
    self.heapify_up()

  def find_max(self):
    if self.length == 0:
      return None
    else:
      return self.A[0]
  
  def delete_max(self):
    if self.length == 0:
      return None
    else:
      self.A[0] = self.A.pop() # 마지막 leaf node를 root node 로 보냄
      self.length -= 1  
      self.heapify_down(0) # root node 부터 heapfipy_down 시행 
  

print('==' * 20)
print('MaxHeap')
arr = [2,6,5,1,3,0,7]
print('정렬 안된 이진 트리 : ', arr)
a = MaxHeap(L = arr)
print('현재 힙 성질을 만족하는 이진 트리 : ',a.A)
a.insert(7)
print('7 insert 이후 이진 트리 :', a.A)
print('find_max : ',a.find_max())
a.delete_max()
print('delete max 이후 값 : ',a.A)

추가

search 기능은 왜 없나요 ?

배열 과 연결리스트 등과 달리 heap 은 정렬 되어 있지 않기 때문에 따로 search 기능은 불가능하다 .

find_max 기능은 있는데 find_min 기능은 없나요 ?

이번에 실습한 heap 의 힙 성질은 부모노드가 자식노드보다 값이 크는 힙 성질을 만족하는 max_heap을 만들었기 때문에 root node 가 가장 큰 값이 되어 find_max 기능을 존재하게 했다.

만약 find_min 기능을 만족하게 만들고 싶다면 힙성질 을 변경 시켜 부모노드가 자식노드보다 값이 작도록 만드는 min_heap 을 만들면 된다.

MinHeap

class MinHeap:

  def __init__(self, L = []):
    self.A = L 
    self.length = len(self.A)
    self.make_heap()

  def heapify_down(self, k):

    n = self.length
    while 2 * k + 1 < n: # leaf node가 존재하지 않는 경우까지 반복
      L,R = 2 * k + 1 , 2 * k + 2
      # K,L,R 비교하기
      if self.A[k] > self.A[L]:
        m = L 
      if self.A[L] > self.A[R]:
        m = R
      # 만약 값을 MinHeap 성질을 만족하지 못해 swap 해야 한다면
      if m != k:
        self.A[m] , self.A[k] = self.A[k] , self.A[m]
        # swap 후 swap 한 값에 대해서 내려가며 반복문 수행 
        k = m 
      else:
        break

  def make_heap(self):
    n = self.length

    for k in range((n + 1 // 2), -1 , -1):
      self.heapify_down(k)

  def heapify_up(self):
    k = self.length  - 1 

    # leaf node 에 대한 heapify_up 할 것이니까 leaf_node의 인덱스는 
    # self.legnth - 1

    while k > 0 and self.A[(k - 1) // 2] > self.A[k]:
      # root node 가 아니면서 자식노드가 부모노드보다 값이 작을 때 시행
      self.A[k] , self.A[(k-1) // 2] = self.A[(k-1) //2] , self.A[k]
      k = (k-1) // 2

  def insert(self,value):
    self.A.append(value)
    self.length += 1 
    self.heapify_up()

  def find_min(self):
    if self.length == 0:
      return None
    else:
      return self.A[0]

  def delete_min(self):
    if self.length != 0: # heap 이 비어있지 않다면
      self.A[0] = self.A.pop()
      self.length -= 1
      self.heapify_down(0)

print('==' * 20)
print('MinHeap')
arr = [2,6,5,1,3,0,7]
print('정렬 안된 이진 트리 :' , arr)
b = MinHeap(L = arr )
print('현재 힙 성질을 만족하는 이진 트리 : ',b.A)
b.insert(-1)
print('-1 insert 이후 이진 트리 :', b.A)
print('find_min : ',b.find_min())
b.delete_min()
print('delete min 이후 값 : ',b.A)

========================================
MinHeap
정렬 안된 이진 트리 : [2, 6, 5, 1, 3, 0, 7]
현재 힙 성질을 만족하는 이진 트리 :  [0, 1, 2, 6, 3, 5, 7]
-1 insert 이후 이진 트리 : [-1, 0, 2, 1, 3, 5, 7, 6]
find_min :  -1
delete min 이후 값 :  [0, 1, 2, 6, 3, 5, 7]