def fibo(n : int) -> int:
  if n <= 1:
    return n 
  else:
    return fibo(n-1) + fibo(n-2)

일반적으로 재귀함수로 피보나치 수열을 구현하면 다음과 같다.

하지만 이는 n 이 어느정도 작을 때에는 시간이 오래 걸리지 않지만 n이 50만 넘어가도

매우 느리게 작동하는 모습을 볼 수 있다.

그 이유는 재귀 함수 특성상

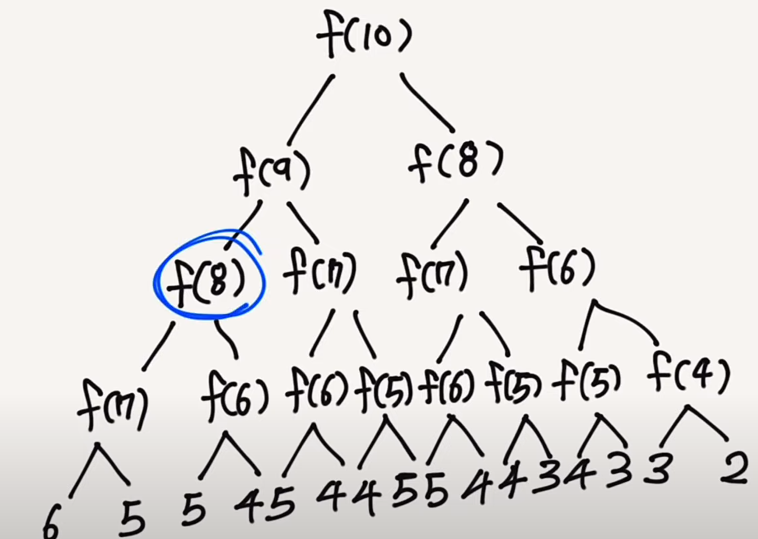
fibo(10) 을 구하기 위해서 반복적으로 수 들을 탐색해나가는 특성으로 인해서 발생한다.

어떤 노드에서 fibo(1) , fibo(2) 를 구해서 위로 올라가면 될 것 같지만

가장 맨 왼쪽에 위치한 fibo(9) -> fibo(8) -> fibo(7) -> fibo(6) .. 노드 들이 fibo(1) , fibo(2) 를 만날 때 까지 쭉 내려간 후에 끝까지 내려 간 후부터 위로 올라가며 연산이 될 것이다.

이런 느낌이라고 해야 할까 ..

이는 불필요한 재귀 함수가 마지막 레벨에 도달 할 때 까지 지속적으로 반복된다는 것이다.

메모리제이션 재귀함수

def memo_fibo(n : int) -> int:
  if n in memo:
    return memo[n]
  else:
    temp = memo_fibo(n-1) + memo_fibo(n-2)
    memo[n] = temp
    return memo[n]

재귀함수의 메모리제이션 은 중복되는 계산을 피하기 위해 이 전에 계산한 값을 저장하고 재활용 하는 기술이다.

특히 동일한 입력에 대한 함수 호출이 여러번 발생 할 때 유용하다.

에서 보면 이미 레벨 5단계 까지만 가도 f(0) , f(1) , f(2) , f(3) , f(4) , f(5) 는 구해놨기 때문에

레벨 6단계만 가도 이미 f(0) ~ f(5) 까지 알고 있기 때문에 불필요하게 깊어질 필요 없이 연산을 종료 할 수 있다.

$N$ 이 있을 때 예전엔 깊이가 $N$ 이 될 때 까지 재귀 함수를 반복했어야 했다면

메모리제이션 을 사용하게 되면 $N // 2 + 1$ 단계 까지만 확인하고도 반복을 끝낼 수 있다.