Introduction

---

목표

---

• 이 논문에서의 목표는 TKG를 다루는 CyGNet(Temporal Copy Generation Network) 모델을 만드는 것이다.
• CyGNet은 link prediction을 위한 모델이며 우리가 일반적으로 알고있는 과거에 기반한 미래예측을 넘어 과거에 일어나지는 않았지만 일어날 수도 있는 사건까지 포착하는 역할을 한다는 점에서 큰 이점이 있다

TKGE 모델의 한계

---

• 기존의 TKGE모델들은 시간 벡터를 학습하기 때문에 장기간의 시간을 학습하는데에는 한계가 있다.
• 조금 더 들여다 보면 이 모델들은 일반적으로 선형 모델로 비선형적인 변화들을 예측하는 데에는 무리가 있고 대부분의 TKGE모델들은 각 시점을 독립적으로 학습하기 때문에 연속적인 내용을 담아내는데에는 무리가 있다.
• 또한 여러 시간 벡터를 하나의 고정된 차원의 공간에 표현해야하기에 시간이 늘어날 수록 시간 벡터의 고유성이 줄어들 수도 있다.
• 실제로 실제 세계의 사건들은 과거의 사실에 기반하여 재발하거나 주기성을 가지며 발생하는데 이러한 내용을 다루기 위해서는 새로운 모델이 필요하다.

배경

---

Static KGE

• 시간적 정보가 없는 KGE는 분명한 한계가 있었다

TKGE

• TTransE를 필두로 기본적인 시간 정보를 포함한다는 점에서 TKGE는 좋은 아이디어였으나 장기간의 그리고 반복적인 패턴을 학습하는데에는 분명한 한계가 존재하였음
• 또한 이를 보완하기위해 GCN, RNN을 결합한 모델들이 등장하였지만 이는 계산량이 매우 크다라는 단점을 가지고 있음

Copy Mechanism

• 이때 NLG에 사용되는 Copy Mechanism이라는 기술이 있고 이 기법을 그래프에 적용하는 방식을 제안한 최초의 모델이 CyGNet임

CyGNet

---

Notation

---

• relation : $p \in \mathcal{R}$
• subject : $s \in \mathcal{E}$
• object : $o \in \mathcal{E}$
• time : $t \in \mathcal{T}$
• graph : $\mathcal{G} = \{ {\mathcal{G}_1,\mathcal{G}_2,...,\mathcal{G}_T} \}$ - 전체 그래프는 각 시간대 별의 그래프를 모두 포함한다.
  • $\mathcal{G_{(t_1,t_{k-1})}} = \{ {\mathcal{G}_1,\mathcal{G}_2,...,\mathcal{G}_{k-1}} \}$ : 다음과 같은 표현하여 특정시간 사이의 모든 그래프를 표현
• $g = (s,p,o,t)$ : 각 quadruple은 다음과 같이 표현된다.
• $H_{t_k}^{(s,p)}$ : $t_k$시점 이전에 나온 $(s,p)$쌍에 대한 object들이 나왔는지를 N차원 multi-ont-hot vector로 표현한 것이고 이 때 N은 $\mathcal{E}$의 cardinality가 된다. 이전에 나왔던 값은 1 한 번도 나온적 없는 값은 0이 될 것이다.

Main Idea

---

• 기본적으로 Copy mode와 Generation mode를 결합한 방식의 모델이다
• Copy mode는 이전에 나왔던 값들을 기반으로하여 미래에 나올 값을 예측하는 것이고 Generation mode는 이전에는 나오지 않았지만 나올 수도 있기 때문에 나올 것으로 기대되는 값들을 예측하는 모델이다.

example

• $H_{t_K}^{(s_1,p_3)} = \{s_3,s_9,...\}$ 라면 Copy mode에서는 이 값들에 확률을 주고 Generation mode는 모든 가능한 entity들에게 확률을 준다 그 후 이를 결합하여 최종 예측을 하게된다.
• 이때 학습과정에서 $(s_1,p_3)$쌍이 시간에 따라 Copy하는 특성을 많이 보였다면 Copy mode 값에 가중치를 더 줄 것이고 반대로 무작위적으로 발생하는 경향이 크다면 Generation mode에 더 많은 가중치를 주게 될 것이다.

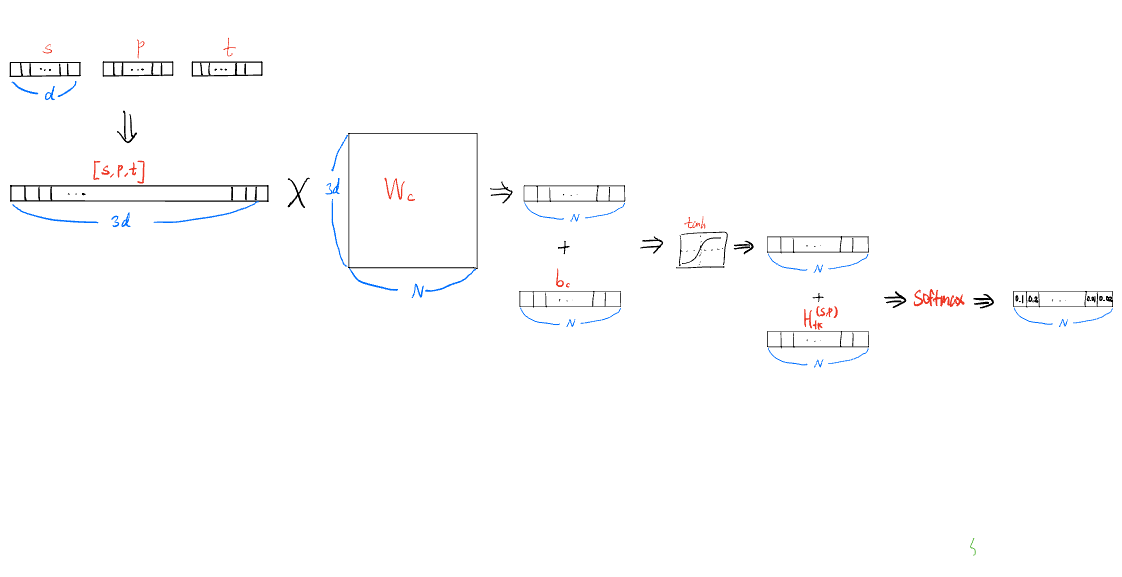
Copy Mode

---

1. $s,p,t_k$는 각각 d차원의 벡터로 임베딩 된다
2. 이를 $W_c$의 가중치행렬과 연산을 한 후 $b_c$의 편향을 추가하고
3. 이를 tanh를 이용하여 비선형 변환을 한다.

1. 위에서 구한 $v_q$와 이전에 우리가 가지고 있는 $H_{t_k}^{(s,p)}$를 이용하여 새롭게 값을 업데이트 한다.

   1. 이때 $H_{t_k}^{(s,p)}$는 원핫 벡터가 아니라 조금 수정하여 copy mode에서는 이전에 나오지 않은 값들에 대해서는 큰 관심이 없기 때문에 0인 값들은 특정한 음수값으로 바꾸어준다.

   💡이 특정한 값에 대해서는 논문에서는 자세히 기록하지 않았음

2. 그 후 이 값들을 softmax를 통해 정규화하여 각 entity가 나올 확률을 구할 수 있다.

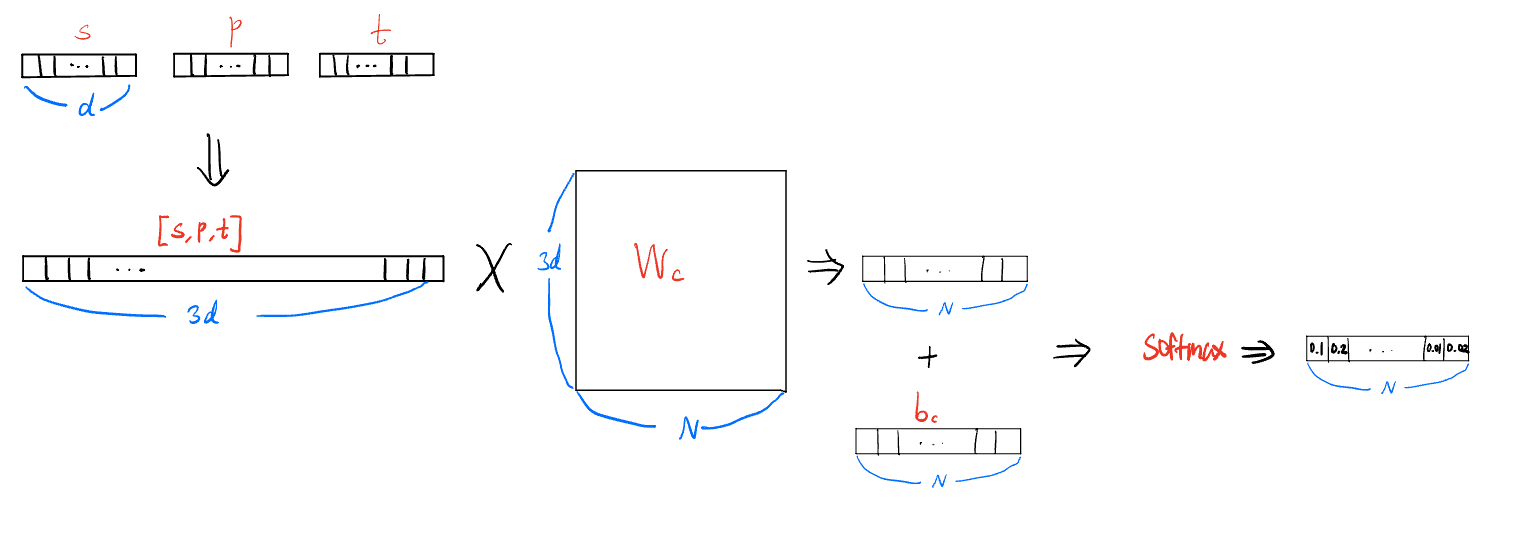
Generation mode

---

• 이전에 본 copy mode와 작동방식은 동일하나 히스토리벡터가 없는 형태라고 볼 수 있다.

Inference

---

• 두 mode를 통합하여 사용하는데 이 때 $\alpha$값을 통해 copy mode와 generation mode에 각각 가중치를 부여할 수 있다.
• 그리고 통합한 값 중 가장 큰 값을 예측 값으로 사용 가능하다.

Loss Function

---

• vocabulary에 존재하는 특정 s,p에 대해 loss function을 구하는 것이다.
  • 이 때 s,p,t 쌍으로 따로 학습하게되면 학습과정에서 순차적인 t의 흐름을 포착하지 못할 가능성이 있기에 함께 학습 시켜준다
• cross entropy를 이용하여 실제 정답레이블의 확률을 높이는 방향으로 학습한다.

Experiment

---

• 실제 여러 데이터 셋들로 기존의 Static, Dynamic한 model들과 테스트해본 결과 거의 모든 부분에서 CyGNet이 좋은 성능을 보였다.
• 특히나 temporal 속성이 없는 static model에 비했을 때는 굉장히 높은 성능을 보여주었다.

Conclusion

---

• 이 연구에서 가장 중요한 점은 과거 사실을 기반으로 미래를 예측한다라는 것이고 그 다음은 새로운 사실에 대해서도 예측이 가능하다는 것이다.
• 후속 연구로는 copy mechanism을 넘어서 중요한 사건들을 추출하여 그것을 주된 예측으로 삼는 것에 대해 열어 놓았고 자연어 처리에서 발생하는 동적인 사건들을 이해하고 분석하는 방법에 대한 연구도 열어 놓았다.