Temporal Knowledge Graph Completion: A Survey

YongUk·2025년 3월 12일
GraphTKG논문분석

논문 분석

목록 보기
5/5

Introduction

  • KGC(Knowledge Graph Completion)을 이용하여 다양한 연구가 진행되고있고 실제로 유의미한 결과를 보여주고 있다.
  • 그럼에도 불구하고 가장 큰 문제는 실제 상황에서 그래프는 정적이기보다 동적인 모습을 보여주는데 KGC는 동적인 부분을 해결해주지는 못한다.
  • 하지만 이러한 시간적 개념없이는 더 정확한 fact를 예측하기에는 한계가 분명히 존재한다.
  • 실제로 2018년 TKGC의 개념이 처음 등장한 이후 KGC보다 성능 좋은 모습을 보여주고 있고 이러한 TKGC의 방법론과 현재의 한계 및 후속 연구에 대해서 논한다.

Background

  • 기본적으로 TKGC에서는 G=(E,R,T,F)\mathcal{G} = (\mathcal{E},\mathcal{R},\mathcal{T}, \mathcal{F})를 사용하여 표현한다.
  • q(s)는 정확성을 평가하는 지표로 이것이 낮아지는 방향으로 optimize하게된다.

Loss function

  • 아래는 대표적으로 많이 사용하는 loss function들이다.
  • 기본적으로 다들 negative sampling을 기반으로 한다

  1. margin ranking loss

    l=∑s∈D[q(s)−1∣Ds−∣∑s′∈Ds−q(s′)+γ]+\mathcal{l} = \sum_{s\in \mathcal{D}}\left[ q(s) - \frac{1}{|D^-_s|}\sum_{s^\prime \in D^-_s}q(s^\prime)+\gamma \right]_+
    • negative sample의 score는 높이는 방향으로 positive sample의 score는 낮추는 방향으로 학습하게된다
    • γ\gamma라는 margin과 max(x,0)max(x,0)라는 제한을 두어 positive와 negative 사이의 간격을 조정해준다

  2. The cross entropy loss

    l=∑s∈Dexp(q(s))∑s′∈Ds−exp(q(s′))\mathcal{l} = \sum_{s\in \mathcal{D}}\frac{exp(q(s))}{\sum_{s^\prime \in D^-_s}exp(q(s^\prime))}
    • 마진이 없어서 위 식과는 달리 일정한 Margin은 보장하지 않는다

  3. Binary cross entropy

    l=∑x∈D∪Ds−yq(x)+(1−y)(1−q(x))\mathcal{l} = \sum_{x \in D \cup D^-_s}yq(x) + (1-y)(1-q(x))
    • x가 positive일 때 y는 1이되고 x가 negative일 때 y는 0이되어 negative의 확률은 높이고 positive의 확률은 줄이는 방향이되고 많이 사용되는 loss function이다.

Benchmark Dataset

  • ICEWS, GDELT dataset이 TKGC에 사용하기 좋은 데이터셋으로 알려져있다. 💡 국제, 사회, 정치의 문제를 담은 데이터셋으로 추후 프로젝트에 이용할 수 있으면 좋을 것 같다.

Evaluation Metric

  • MR(Mean Rank)
    • 모델이 예측한 샘플의 순위의 평균을 말한다
    • ex) (s,p,?,t)에서 예측한 확률 순서대로 {A,B,C,D,E, …}라고 하자 이때 실제 답이 C라면 현재 step의 score는 3이 되고 나중에 이 모든 평균을 구하여 모델의 성능을 평가한다.
    • 1에 가까울수록 좋고 숫자가 커질수록 성능이 나쁘다
  • MRR(Mean Reciprocal Rank)
    • 모델이 예측한 샘플의 순위의 역수를 구하여 이를 평균낸다
    • ex) 위 예시에서 score는 1/3이 될 것이다.
    • 1에 가까울수록 좋고 숫자가 0에 가까워질수록 성능이 나쁘다
  • Hits@k
    • MR, MRR의 한계점은 예측값이 1개일 때 잘 작동한다는 것이다.
    • 이때 (s,p,?,k)에 대한 실제값이 많이 있을 수 있고 이를 해결하기 위한 방법으로 상위 k개에 실제 값이 얼마나 있는지 비율로 나타낼 수 있는 방법이다.

Various Method

  • KGC 그래프에 timestamp가 추가된 TKGC의 형태는 조금 더 복잡하고 이를 위해 다양한 기법이 존재한다.

Tensor Decomposition

  • tensor decomposition은 굉장히 light한 방법이고 학습하기 쉽다.
  • 또한 기본적인 KGC의 tensor decomposition 기법을 조금만 확장시키면 TKGC에 바로 적용시킬 수 있다.

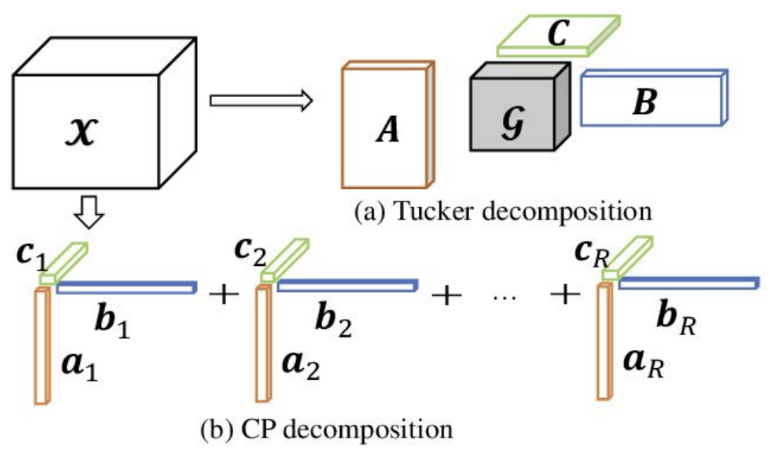
Canonical Polyadic Decomposition

  • 원래의 행렬 3차원 tensor를 A,B,C 3개의 tensor로 나눌 수 있다. 이 때 TKG에서는 각각이 (h,r,t)가 될 것이다.
X≈∑α=1dA:,α⊕B:,α⊕C:,α\mathcal{X} \approx \sum_{\alpha=1}^dA_{:,\alpha}\oplus B_{:,\alpha}\oplus C_{:,\alpha}
  • 위 식을 기반으로 학습하게 되고 이 때 새로운 값에 대한 예측을 하기 위해서는
Xijk≈∑α=1daiαbjα ckα\mathcal{X}_{ijk} \approx \sum_{\alpha=1}^da_{i\alpha} b_{j\alpha}\ c_{k\alpha}
  • 다시 내적을 하여 이 값을 기반으로 예측을 수행할 수 있다.
  • 이를 확장하여 temporal 속성을 넣은 quadruple을 학습하고 싶다고 하면
X≈∑α=1dA:,α⊕B:,α⊕C:,α⊕D:,α\mathcal{X} \approx \sum_{\alpha=1}^dA_{:,\alpha}\oplus B_{:,\alpha}\oplus C_{:,\alpha}\oplus D_{:,\alpha}
  • 다음과 같이 간단하게 수정할 수 있다.

Tucker Decomposition

  • CPD의 일반화된 형태라고 볼 수 있는데 CPD의 경우는 각 tensor의 rank가 모든 matrix에 대해 일정하다.
  • 하지만 Tucker Decomposition은 각 A,B,C의 rank가 다 다를 수 있다
Xijk=∑α=1d1∑β=1d2∑γ=1d3Wαβγaiαbjβckγ\mathcal{X}_{ijk}=\sum_{\alpha=1}^{d_1}\sum_{\beta=1}^{d_2}\sum_{\gamma=1}^{d_3}\mathcal{W}_{\alpha \beta \gamma}a_{i\alpha}b_{j\beta}c_{k\gamma}
  • 따라서 다음과 같이 W인 core-tensor를 추가하여 중재하는 역할이 필요하지만 각 특성에 따라 더 세부적인 학습을 가능하게 한다.

CPD vs TD

  • CPD는 단순화된 형태이기 때문에 계산속도는 좋으나 성능은 TD보다 떨어질 수도 있다.
  • TD는 CPD보다 정보량이 많아 더 다채로운 결과를 보여줄 수 있지만 연산량이 많아 복잡하다.

Timestamp-based Transformation

  • 이번에는 변환과 관련된 방식이다

Synthetic Time-dependent Relation

  • 가장 기본적인 방식으로는 q(s)=∥eh+u(r,T)−et∥q(s) = \|e_h+u(r,\mathcal{T})-e_t \| 와 같이 관계와 시간을 합성하여 나타내는 방식이 있다.
  • 이 방식은 time의 interval 속성은 다루지 못하기 때문에 이를 다루기 위해 CPD(change-point-detection) 방식을 이용한 Splitting과 Merging을 이용한 기법도 고안되었다.
  • 복잡한 시간 표현을 나타내기 위해 self-attention을 활용한 3DRTE 모델도 존재함 💡 3drte: 3d rotation embedding in temporal knowledge graph 나중에 이 논문 한 번 보면 좋을 것 같음

Linear Transformation

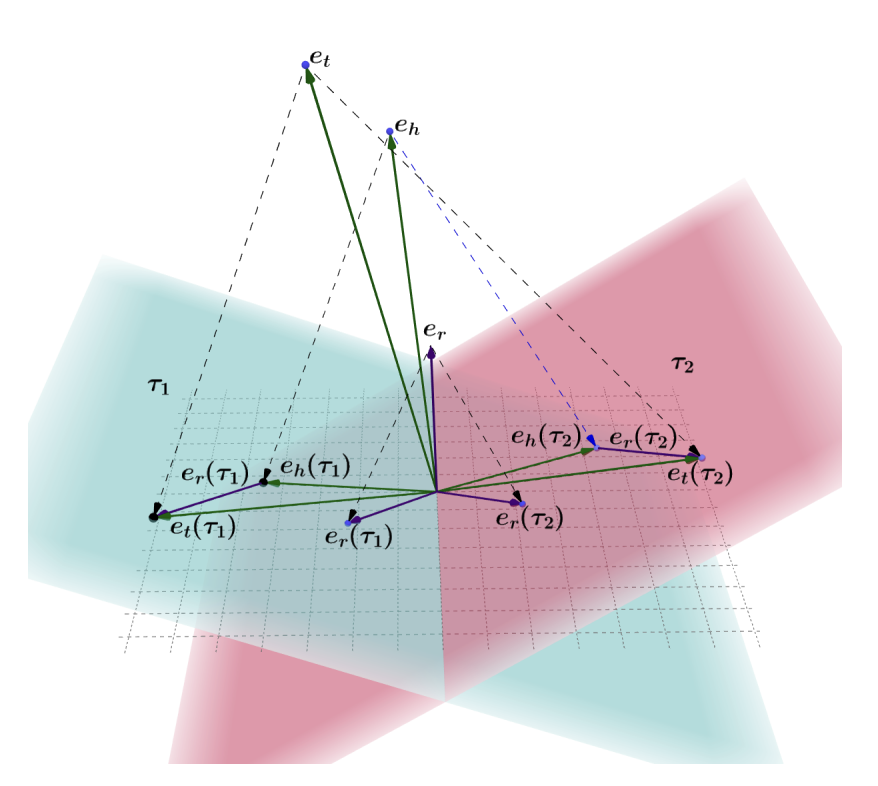
  • HyTE
    • 각 timestamp를 특정 hyperplane으로 만들어 triple을 이에 투영시켜 구체적인 값을 찾는 방식이다.
    • P(e)=e−wTTewT\mathcal{P}(e) = e-\mathcal{w}^T_{\mathcal{T}}e\mathcal{w}^T를 최소화 하는 방향으로 임베딩을 진행하게 되고
    • 실제로는 q(s)=∥P(eh)+P(er)−P(et)∥q(s)=∥P(e_h)+P(e_r)−P(e_t)∥의 손실을 계산한다.

  • Hybrid-TE
    • 위 HyTE 모델은 multi-relations들을 다루지 못하기 때문에 TransD와 HyTE를 결합하여 각각 multi-relation과 temporal 속성을 다루는 것을 가능하게 하는 모델이다.
  • TeRo
    • 복소 공간에서 회전을 이용하여 시간적 속성을 표현하는 모델이다

Dynamic Embedding

  • 위의 임베딩 기법들을 이용하여 시간을 표현하는 것은 가능하나 시간 흐름에 따른 변화를 포착하는데에는 한계가 있다.
  • 따라서 이러한 특성을 포착하기위해 dynamic embedding을 사용한다.

Representation as Functions of Timestamp

  • ATiSE
    e=estatic+trend(T)+seasonal(T)+Ne = e_{static}+trend(\mathcal{T})+seasonal(\mathcal{T}) + \mathcal{N}
    • 기본적으로 정적인 특성에 시계열적인 특성 trend와 sensonal를 추가하여 조금 더 과거를 반영한 예측이 가능하다
  • DyERNIE
    • 기존의 유클리드 공간에서의 한계점을 보완하고 비유클리드적 특성을 찾기 위해 비유클리드 임베딩을 하는 기법이다.
  • Diachronic Embedding
    • 자세한 논문을 읽어보지는 않았지만 기존의 KG 모델에 합쳐서 사용할 수 있는 기술이고 논문에서는 SimpleE라는 모델과 결합하였을 때 성능이 가장 좋다고 한다.

RNN

  • Know-Evolve
    • RNN을 통해 더 깊은 관계를 찾아 학습할 수 있다라는 것을 제시함
  • TeMP
    • GCN과 RNN을 결합한 방법으로 볼 수 있다
    • Structural Embedding을 이용하여 구조를 학습한 후 Temporal Embedding을 이용하여 시간에 따른 구조의 변화를 학습한다.
    • 이때 SE를 위해 GCN을 사용하고 TE를 위해 GRU혹은 Self-Attention을 사용한다.

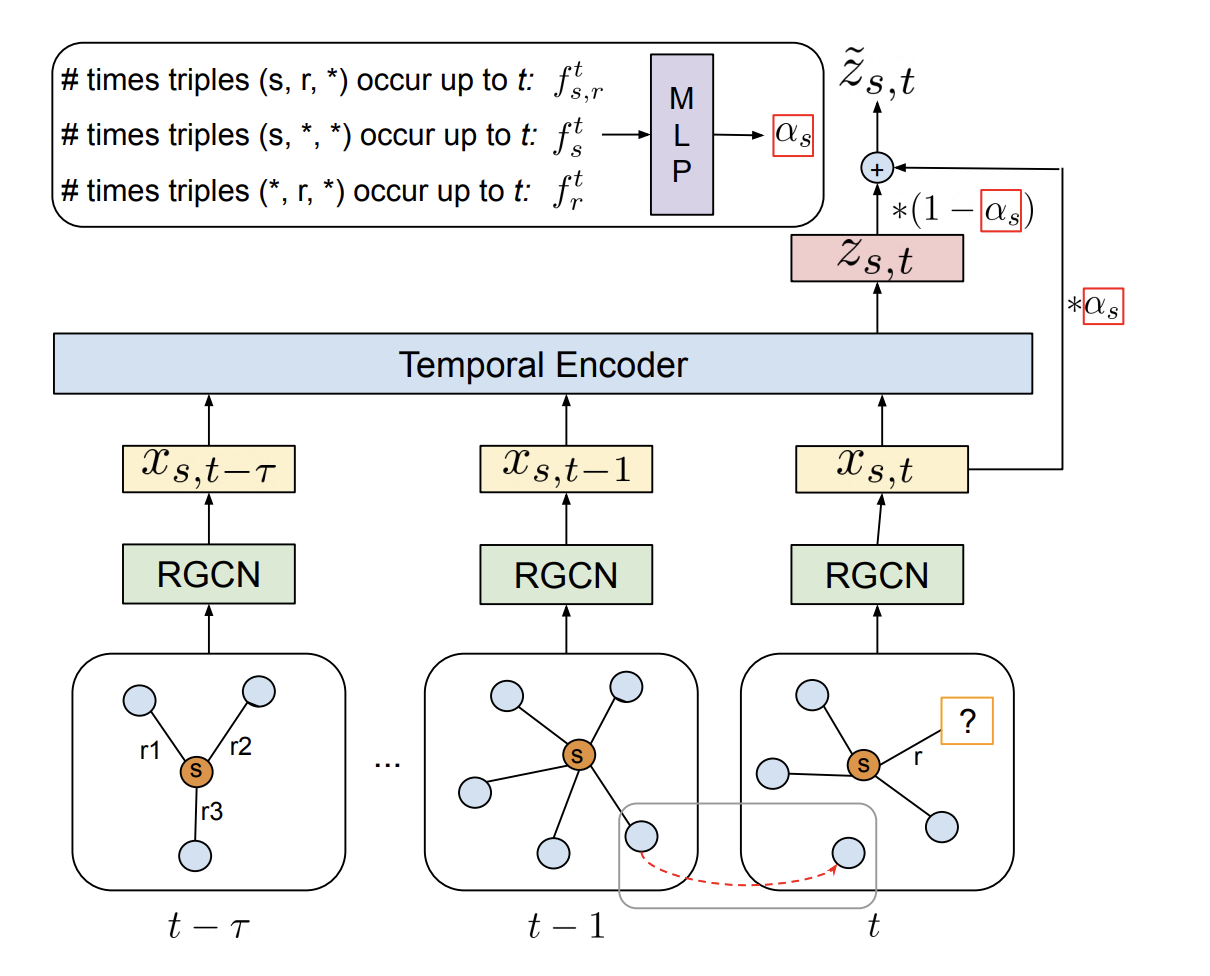
Learning From Knowledge Graph Snapshots

  • 시간에 따라 이전 그래프가 그 다음 시간의 그래프 형성에 영향을 주도록 학습하는 기법이다.

Markov Process Models

  • RTFE
    • 각각의 subgraph들이 1차 마르코브 체인을 따른다는 것을 가정한 모델이다

Autoregressive Models

  • Re-Net
    • 자기회귀 방식을 이용하여 시간에 따른 그래프를 학습하는 기법이다.
  • RE-GCN
    • GCN을 활용하여 발생하는 사실 간의 의존성을 학습한다.
  • TANGO
    • NODES 방식을 사용하여 그래프의 동적 변화를 학습하는 방식이다.

Reasoning with Historical Context

  • 과거의 데이터에서 유의미한 정보를 찾아 link prediction을 하는 방식이다.

Attention-based Relevance

Heuristic-based Relevance

미래 연구 방향

  1. 외부 지식 결합
    • 데이터에 부족한 부분을 보완하여 데이터 불균형을 해소한다
  2. 시간 정보를 활용한 Negative Sampling
    • 현재 negative sampling에 시간정보를 고려한 정보를 포함하여 negative sampling을 진행하는 방향이 중요하다
    • 또한 GAN 방식을 활용하여 조금 더 정교한 예측을 가능하게 한다
  3. 대규모 데이터셋 적용
    • 큰 규모의 데이터셋에는 이를 적용하기 어렵기 때문에 이러한 부분들에 대한 보완이 필요하다
  4. 진화하는 지식 그래프
    • 계속해서 발전하는 지식 그래프의 원활한 학습을 위해 온라인 학습 기법이 개발되어야한다.
profile
YongUk
이전 포스트

Learning from History:Modeling Temporal Knowledge Graphs with Sequential Copy-Generation Networks

0개의 댓글