[Network Science]1. Introduction to network science

---

그래프 용어 정리

---

그래프는 크게 가중치의 존재 여부와 방향성의 존재 여부에 따라 directed, weighted 그래프로 분류 가능하다

Undirected Graph

$k_i = |N(v_i)|$ : incident edges의 수 (Neighbor의 수) = degree

$\langle k \rangle = \frac{\sum k_i}{n} = \frac{2m}{n} = \frac{2|E|}{|V|}$ : Average of degree - 전체 그래프의 특성을 표현할 때 사용한다

일반적으로 대문자 E는 edge의 전체 집합이고 e는 각각의 edge를 표현할때 사용한다

Directed Graph

$k_i= k_i^{in} + k_i^{out}$

$\langle k_i^{in} \rangle =\langle k_i^{out}\rangle = \frac{|E|}{|V|}$

directed graph는 in-degree, out-degree로 종류가 두가지 이므로 이를 따로 계산해주어야 함

Degree Distribution

$P(k_i=k) = \frac{n_k}{\sum_k n_k} = \frac{n_k}{n}$ : 각 vertex들의 degree의 분포를 나타내는 방법이다

Average Path Length

$\langle L\rangle = \frac{1}{n(n-1)}\sum_{i\ne j} d_G(v_i, v_j)$ : graph의 각 vertex들의 평균 거리

Graph Diameter

$D = max_{i,j}d_G(v_i,v_j)$

그래프의 규모 = 최단거리 중 최대인 것 (최장 지름)

Graph Transitivity

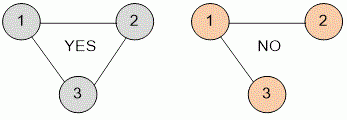
그래프에는 전이성이라는 성질이 있고 이의 정도를 측정하기 위한 클러스터링 계수가 존재한다

전이성은 A-B, B-C가 친구일 때 A-C가 보통 친구라는 뜻이다. 소셜 네트워크에서는 이러한 관계가 잘 설명된다.

이러한 성질은 클러스터링 계수를 이용하여 측정할 수 있고 이 계수를 통해 그래프의 군집성을 파악할 수 있다

이 군집성을 통해 그래프가 군집화가 얼마나 잘 일어날지 예측해볼 수 있다.

전역적 의미

clustering coefficient = $\frac{3 \times triad(number \ of \ triange)}{number \ of \ connected \ triplets \ of \ vertices}$

그래프 전체에서 삼각형이 될 수 있는 것 중 실제 존재하는 삼각형의 비율이다

지역적 의미

$C_i = \frac{N_i사이의\ 연결의\ 수}{\frac{k_i(k_i - 1)}{2}}$ : 이웃 노드들이 서로 모두 연결될 수 있는 경우의 수 중에 실제 연결된 비율

$C = \frac{1}{n}\sum_{i=1}C_i$ : 노드들의 클러스터링 계수의 평균