[Network Science]2. Power Law and Scale-free networks

YongUk·2025년 1월 19일

GNN Graph network science

Graph Theory

목록 보기

4/17

Introduction

초기에 연구자들은 Network의 degree가 random하게 분포하고 degree distribution이 포아송 분포를 따를 것으로 기대하였다.
실제 network를 분석하였을 때 이는 다른 결과를 가져왔고 현재는 Power law distribution을 따른다고 알려져있다.

Power Law Degree Distribution

P_k = Ck^{-\gamma}

\log P_k = -\gamma \log k + \log C

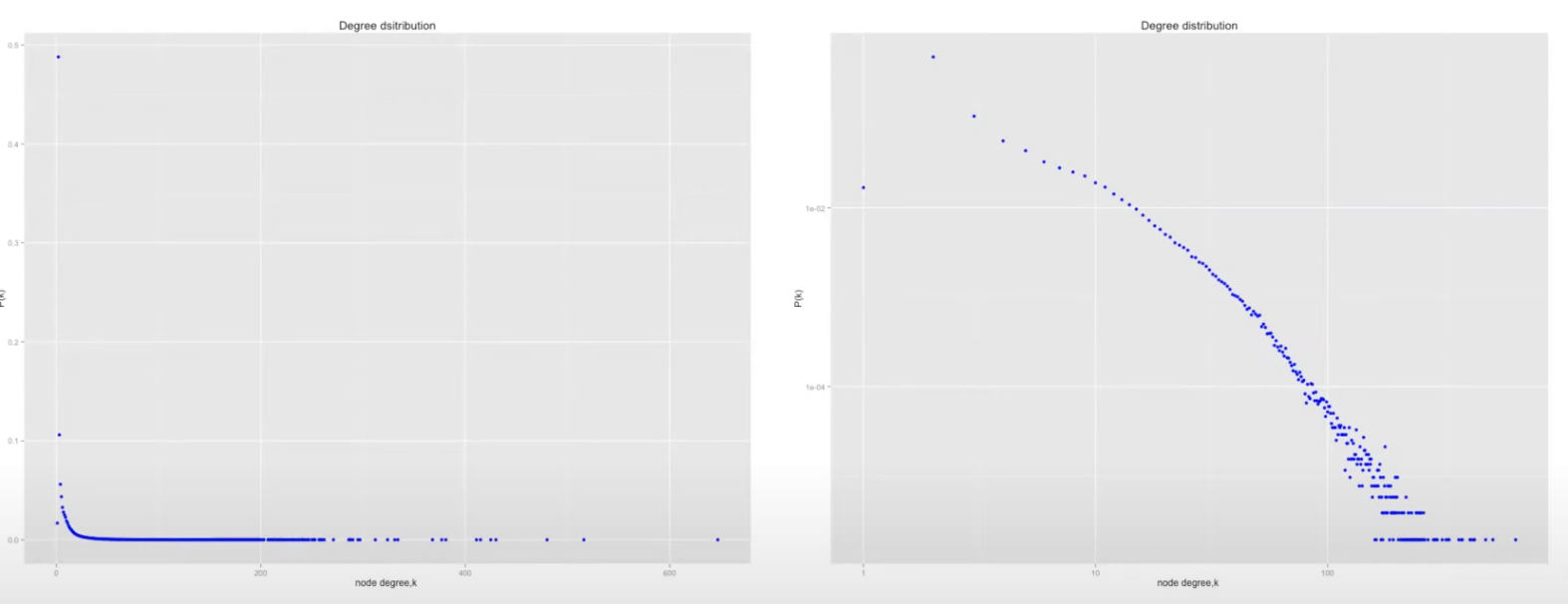
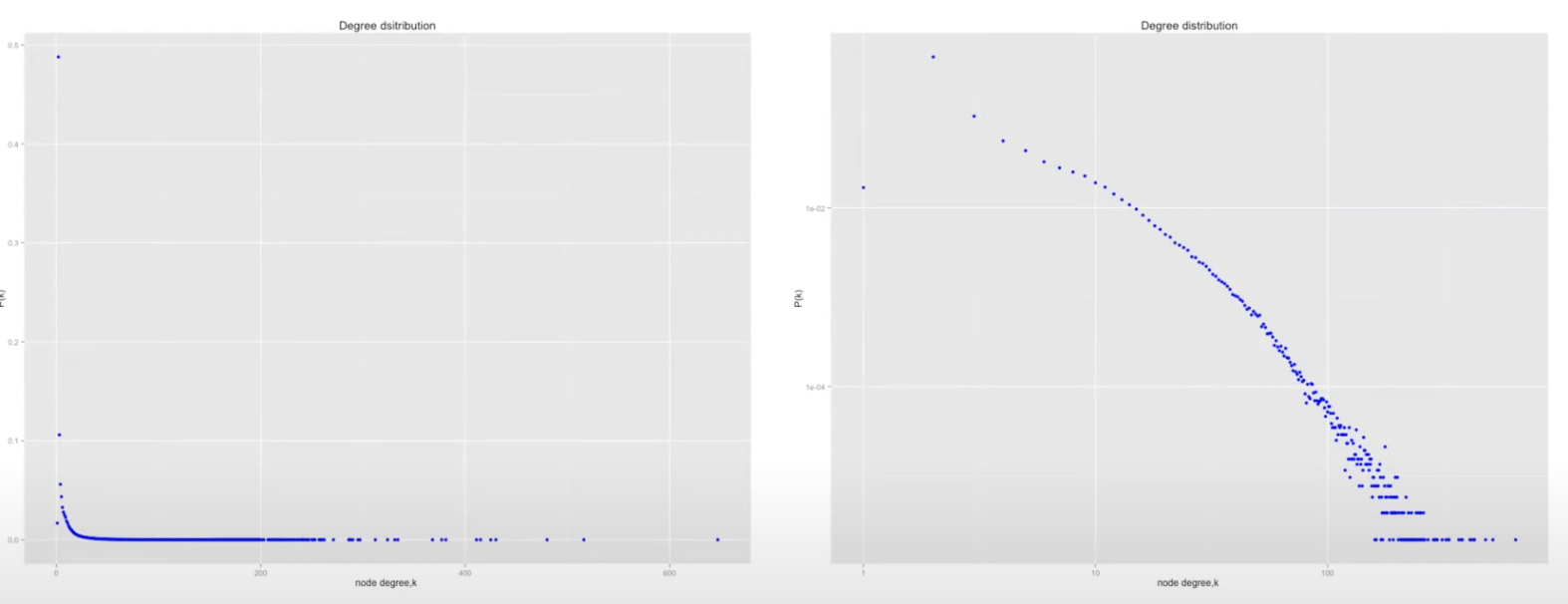
실제 분포는 다음과 같이 정리할 수 있다. 그리고 이는 각각 다음과 같다.
왼쪽이 실제 그래프의 분포이지만 값을 보기 힘들다 따라서 로그 스케일을 취하게 되면 값들을 훨씬 더 쉽게 분석할 수 있다.

Discrete Power Law

위 식을 조금 더 일반화 시켜보면

\sum^{\infin}_{k=1}P_k = C\sum^{\infin}_{k=1}k^{-\gamma} = C\zeta(\gamma) = 1 , \ C=\frac{1}{\zeta(\gamma)}

P_k = \frac{k^{-\gamma}}{\zeta(\gamma)}

다음과 같이 나타낼 수 있다.
하지만 이 이상으로 값을 구하기 위해서는 제타 함수를 풀어야하고 이 과정은 굉장히 까다롭기 때문에 편리하게 적분을 사용할 것이다.
적분을 사용하기 위해서는 현재의 이산형 확률 분포를 연속적인 표현으로 변환시킬 필요가 있다.

Power Law Continuous Approximation

먼저 degree가 정수가 아닌 실수의 값이 들어온다고 가정을 하고 시작한다.

1 = \int^{\infin}_{k_{min}}p(k)dk = C\int^{\infin}_{k_{min}}k^{-\gamma}dk = \frac{C}{\gamma-1}k^{-\gamma+1}_{min}

확률 밀도함수를 다음과 같은 방법으로 구해볼 수 있을 것이다.
이때 최소값을 제한하는 이유는 k의 값을 정하지않았을 때 0에 근사하면 발산할 수 있기 때문에 최소한의 값을 정해두게 된다.
또한 이때 $\gamma > 1$ 이라는 조건이 자동적으로 붙게된다. 만약 그렇지 않으면 무한대로 갈수록 수렴하지않고 발산하게 될 것이다.

C = (\gamma-1)k^{\gamma-1}_{min}

p(k) = (\gamma-1)k^{\gamma-1}_{min}k^{-\gamma} = \frac{\gamma-1}{k_{min}}(\frac{k}{k_{min}})^{-\gamma}

연속형으로 가정하였을 때 최종적으로 다음과 같은 PDF을 얻을 수 있다.

Poisson VS Power Law

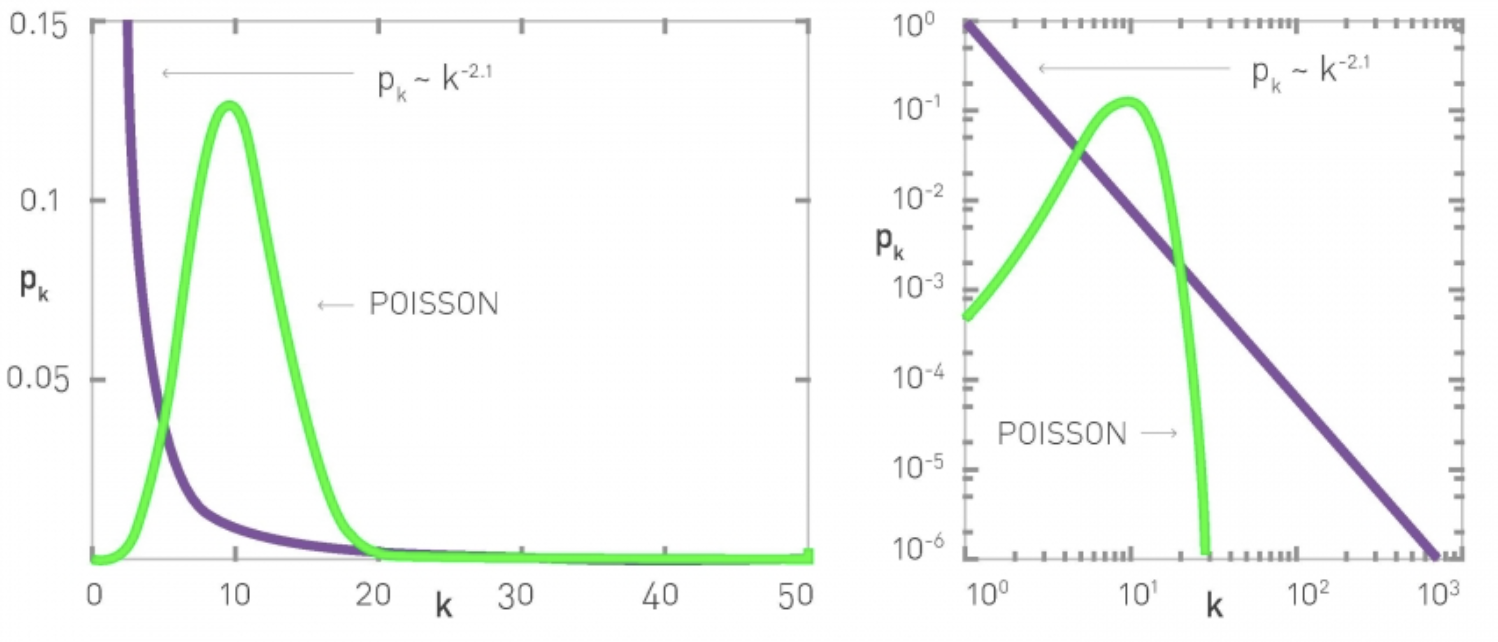
노드가 랜덤하게 연결될 경우에 네트워크의 분포는 포아송 분포를 따르게 될 것이고 이는 랜덤그래프의 성질이자 이전에 사람들이 포아송 분포를 따를 것이라 기대한 이유이다.
포아송 분포와 power law 분포의 가장 큰 차이점은 log scale에서 보여질 수 있다.
포아송은 굉장히 급격한 속도로 0에 도달하는 반면 power law 분포는 일정한 비율로 감소하고 있는 것을 볼 수 있다.
이는 power law 분포에서는 상대적으로 degree 큰 노드들이 많이 나올 수 있다는 것을 보여준다.

Size of Largest Node

최대 차수보다 더 큰 차수의 노드를 가질 확률

Pr(k\ge k_{max}) = \int^{\infin}_{k_{max}}p(k)dk

최대 차수보다 큰 노드의 개수는 1개면 충분하다.

N \times Pr(k\ge k_{max}) = 1

Power law distribution에 따라 위 식을 전개해 보면

N \times \int^{\infin}_{k_{max}}p(k)dk = 1

N \times C\int^{\infin}_{k_{max}}k^{-\gamma}dk = N\times\frac{C}{\gamma-1}k^{-\gamma+1}_{max} = 1

N\times k^{\gamma-1}_{min}k^{-\gamma+1}_{max} = 1

k_{max}= k_{min}N^{\frac{1}{\gamma-1}}

exponential network를 가정하였을 때는 $k_{max} = k_{min} + \frac{\ln N}{\lambda}$ 가 나오게 된다.
이 둘의 증가 속도를 생각해보면 power law distribution이 훨씬 빠를 것이라는 것은 쉽게 알 수 있다. 실제로 아래를 보면 다음과 같다.

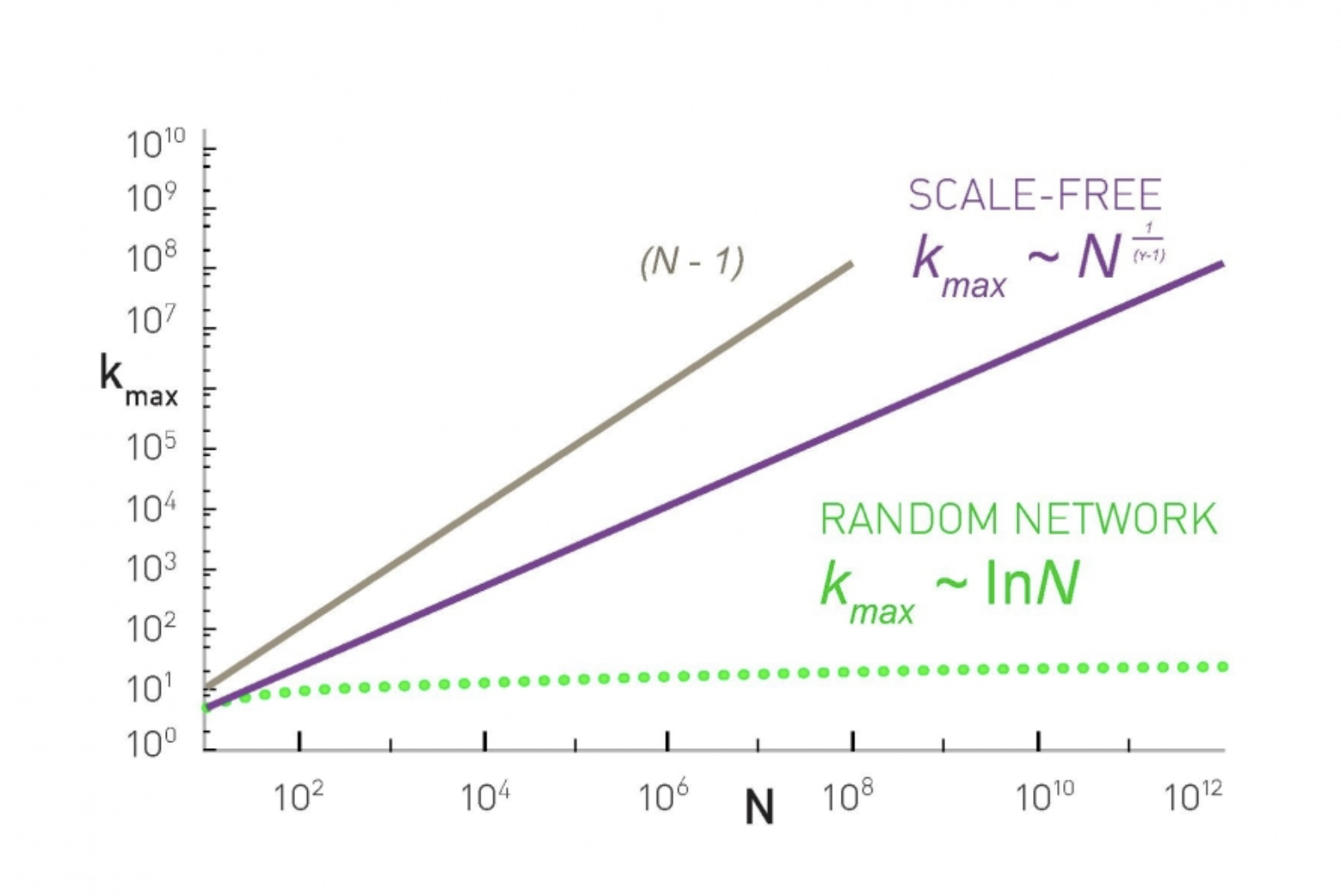
여기서 N-1은 Largest Node가 가질 수 있는 Degree 최대 크기이다.

Moment

통계학에서 모멘트는 모수를 추정할 수 있도록 한다.
1차 모멘트는 해당 분포의 평균을 나타내고 2차 모멘트는 해당 분포의 분산을 나타낸다.

C = (\gamma-1)k^{\gamma-1}_{min}

아래는 1차 모멘트에 대한 전개이다. k의 평균을 구할 수 있는데 이때 항상 이 평균 값이 수렴할까?

\langle k\rangle = \int^{\infin}_{k_{min}}kp(k)dk = C\int^{\infin}_{k_{min}}\frac{dk}{k^{\gamma-1}}

$\gamma > 2$ 를 만족하는 경우에만 수렴하는 평균값을 가지게 될 것이고 이 때 굉장히 간단하게 정의할 수 있다.

\langle k\rangle = \frac{\gamma-1}{\gamma-2}k_{min}

동일한 방법으로 2차 모멘트도 정의할 수 있다

\langle k^2\rangle = \int^{\infin}_{k_{min}}k^2p(k)dk = C\int^{\infin}_{k_{min}}\frac{dk}{k^{\gamma-2}}

이때 2차 모멘트는 $\gamma > 3$ 일 때만 정의가 된다.

\langle k^2\rangle = \frac{\gamma-1}{\gamma-3}k^2_{min}

동일한 방법으로 m차 모멘트는 다음과 같이 일반화할 수 있고 $\gamma > m+1$ 일 때 성립함

\langle k^m\rangle = \int^{\infin}_{k_{min}}k^mp(k)dk = C\frac{k_{max}^{m+1-\gamma} - k_{min}^{m+1-\gamma}}{m+1-\gamma}

Scale-free

위에서 본 1차 모멘트는 평균으로 말할 수 있고 2차 모멘트는 분산으로 말할 수 있다.
이에 따라 $\sigma^2_k = \langle k^2 \rangle - \langle k \rangle ^2$ 로 표준 편차도 정의가 가능하다.
아래는 우리가 일반적으로 포아송 분포를 설명할 때 사용하는 수치이다.

k = \langle k \rangle \pm \sqrt{\langle k\rangle}

일반적으로 power law분포도 다음과 같이 평균과 분산으로 정의할 수 있지만 위에서 보았듯이 1차 모멘트는 정의가 되었지만 2차 모멘트가 항상 정의되는 것은 아니다
만약 1차 모멘트는 정의되었는데 2차 모멘트는 정의가 되지 않았다면 어떻게 될까? 즉 평균은 있는데 분산은 없다면 어떨까?

k = \langle k \rangle \pm \infin

다음과 평균은 존재하지만 변동은 무한하고 정의할 수 있는 특정한 크기가 없어 다음 같이 표현할 수 있을 것이고 우리는 이러한 특성을 scale-free라고 부른다.
$2 < \gamma\le 3$ 를 만족할 때 위와 같은 성질을 보인다. (대부분의 scale-free network가 존재)
만약 $\gamma > 3$ 이어서 분산이 존재한다고 할 예를 들어 $k = 6 \pm 15$ 라는 분포가 있다고 한다면 이때 k는 음수로 가게 되고 사실상 분산의 의미가 사라진다고 생각해도 좋을 것이다. 즉 이러한 경우에도 scale이 존재하지 않는다고 볼 수 있다. 하지만 $\gamma$ 가 너무 커지게 되면 랜덤 그래프와 구분하기 힘들어질 수도 있다.
반대로 $\gamma < 2$ 인 경우는 평균이 발산하고 또한 $k_{max}= k_{min}N^{\frac{1}{\gamma-1}}$ N보다 커지기 때문에 이론적으로 모순이 생긴다. 혹은 만약 있다라고 해도 극단값이 해당 분포를 지배하기 때문에 현실에서는 물리적으로 거의 불가능하다

Estiamting gamma

Case1 CDF

우리는 위에서 아직 감마값을 구하는 방법을 배우지 않았다. 위에서보면 감마는 굉장히 중요한 역할을 하는데 이 감마를 어떻게 구할 수 있을까?

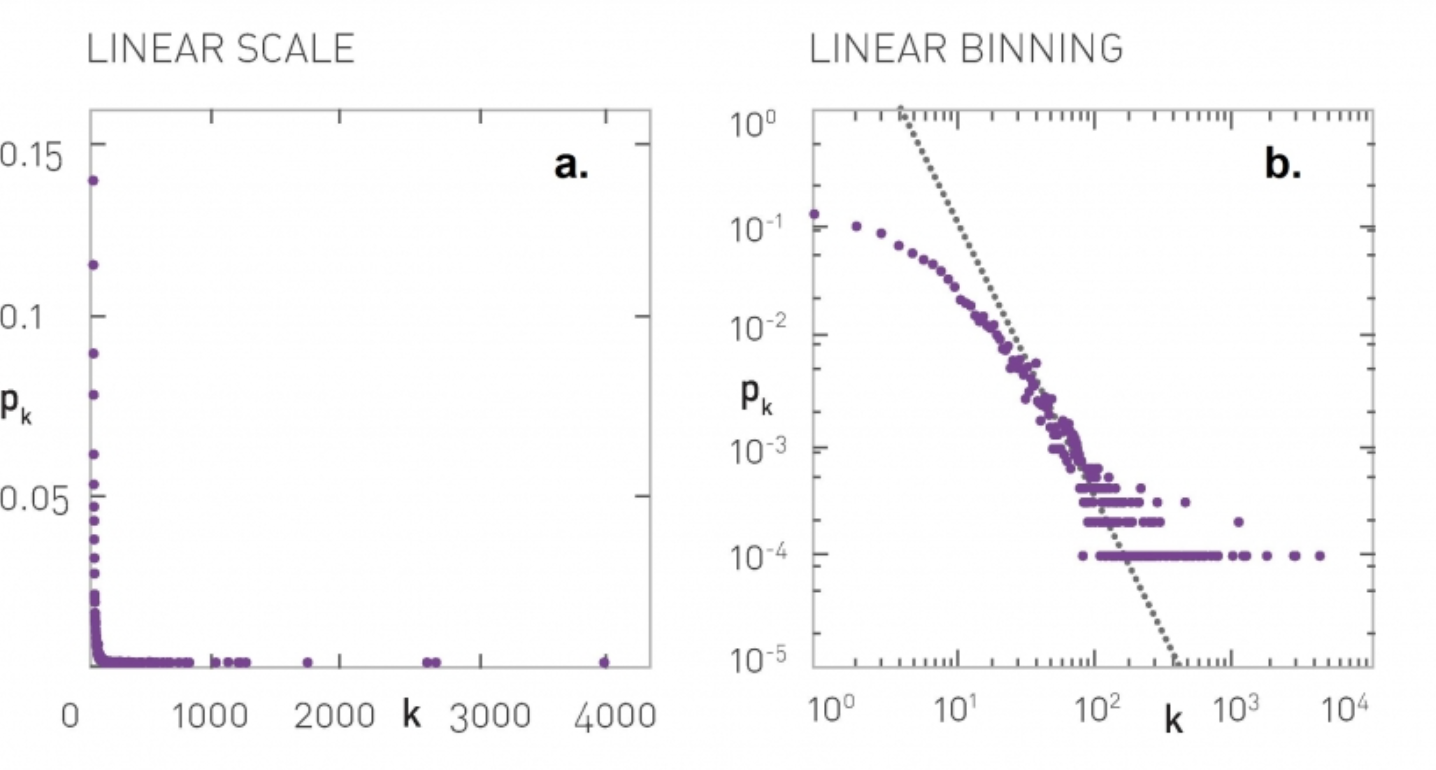
실제 그래프를 로그 스케일로 바꾸면 보통 계단형식을 볼 수 있는 이는 그래프의 특성이며 그럼에도 우리는 아직 어떻게 직선을 그려야할지 정확히 모른다.
따라서 우리는 이것을 일정하게 감소하는 그래프로 변형시킬 필요가 있는데 이때 CDF를 사용할 수 있다.

F(k) = Pr(k_i \le k) = \int^{k}_{0}p(k)dk

다음과 같이 CDF를 나타낼 수 있고 이를 반대되는 개념인 cCDF로 나타내면 다음과 같다

\bar{F}(k) = 1 -F(k) = Pr(k_i > k) = F(k) = Pr(k_i \le k) = \int^{\infin}_{k}p(k)dk

우리는 이것을 이용하면 다음과 같이 일반화 할 수 있다.

\bar{F}(k) = \frac{C}{\gamma - 1}k^{-(\gamma-1)}

log\bar{F}(k) = \log(\frac{C}{\gamma - 1})-(\gamma-1)\log k

이때 기울기는 $\gamma-1$ 이 됨을 알 수 있다.

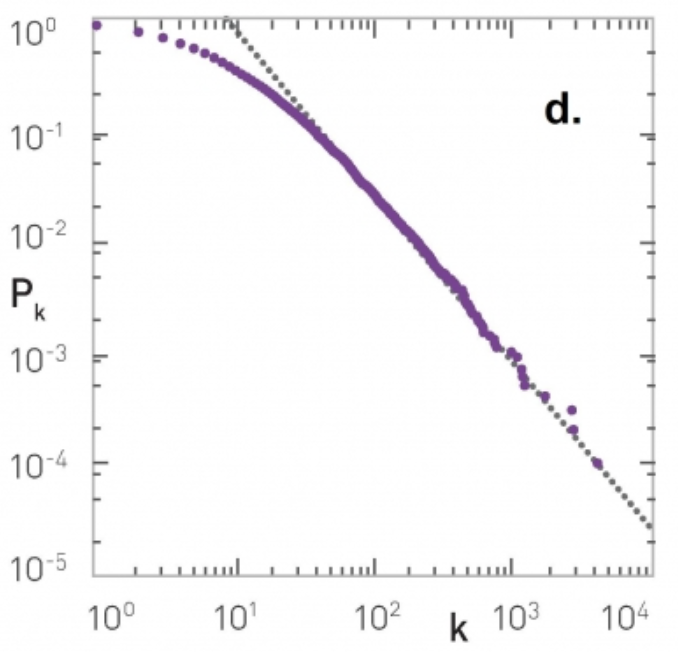
변환하면 다음과 같이 비교적 깔끔한 그래프를 얻을 수 있고 우리는 여기서 기울기를 쉽게 추론할 수 있을 것이다.
다음의 문제는 시작점을 어디로 할 것 인가이다. 위 그림을 보면 $k < 100$ 의 구간에서는 다소 power law 분포를 따르지 않는 것으로 보이고 그 부분을 무시하고 직선을 구하면 깔끔하다.
또한 이 방식은 굉장히 주관적으로 보일 수 있기에 조금 더 수학적이고 정확한 방식을 사용해보겠다.

Case2 Maximum likelihood estimation

우리는 앞서 $p(k_i) = \frac{\gamma-1}{k_{min}}(\frac{k_i}{k_{min}})^{-\gamma}$ 라는 공식을 구했다. 이를 이용하여 감마가 주어졌을때 현재 분포가 나올 확률을 독립시행을 가정하고 조건부확률의 곱셈법칙으로 계산해보면 다음과 같을 수 있다

P(\{k_1,k_2,…,k_n\}∣γ)=\prod_i^n\frac{\gamma-1}{k_{min}}(\frac{k_i}{k_{min}})^{-\gamma}

이를 베이즈 정리로 표현하면 다음과 같다

P(\gamma|\{k_1,k_2,…,k_n\}) = P(\{k_1,k_2,…,k_n\}|\gamma)\frac{P(\gamma)}{P({\{k_1,k_2,…,k_n\}})}

이에 대한 로그 우도함수를 구하면

\mathcal L = \ln P(\gamma|\{k_i\}) = n\ln(\gamma-1)-n\ln(k_{min}) -\gamma\sum_{i=1}^n\ln\frac {k_i}{k_{min}}

이를 최대화하는

\frac{\partial \mathcal L}{\partial\gamma} =0

위를 만족하는 값을 찾는다면

\gamma = 1 + n\left[\sum^n_{i=1} \ln\frac{k_i}{k_{min}}\right]^{-1}

이와 같이 깔끔하게 정리된 식을 얻을 수 있다.

\sigma = \sqrt{n}\left[\sum^n_{i=1} \ln\frac{k_i}{k_{min}}\right]^{-1} = \frac{\gamma-1}{\sqrt{n}}

위와 같이 n이 커지면 오차항은 줄어드는 것을 볼 수 있다. 즉 우리는 최대우도법을 사용하여 기울기를 추정하였다.

Kolmogorov-Smirnov test

아직 우리는 기울기만 구하였고 시작값은 구하지 않았다. 사실 반대로 기울기를 구하기 위해서는 시작값을 구해야한다
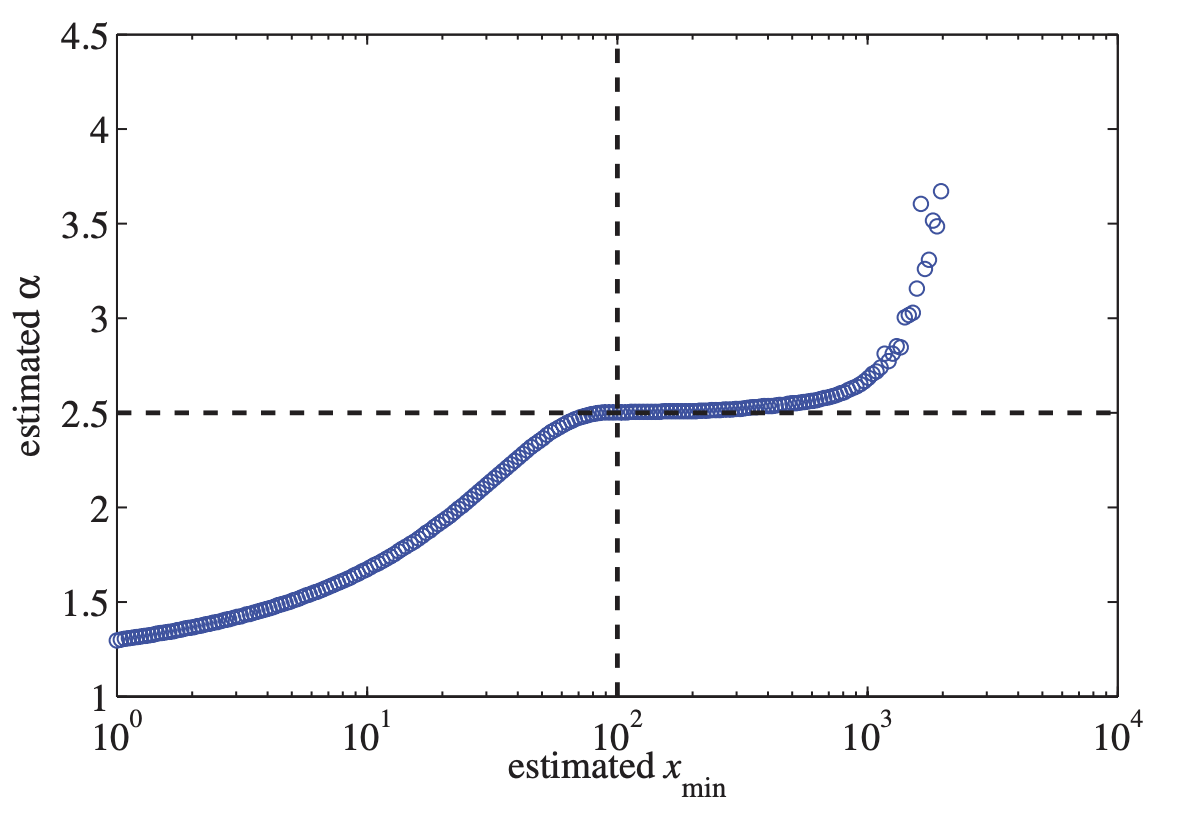
아래 그림을 보면 알 수 있듯이 이 시작값을 어떻게 구하냐에 따라 추정하는 $\gamma$ 가 달라지기때문에 매우 중요하다고 볼 수 있다.
너무 작은 값을 구할경우 편향이 심해져 overfitting이 될 것이고 너무 큰 값을 구할 경우 버려야하는 정보가 많아져 중요한 정보를 지나치게될 수도 있다.
이를 위해 다양한 방법론이 존재하지만 가장 안정적으로 사용할 수 있고 데이터의 크기에 영향을 받지 않는 유명한 방법이 K-S test이다
이는 우리가 구한 모델과 실제 값을 비교하여 그 차이가 최대가 최소가 되도록하는 값을 찾는 것이다.

일단 맨 처음 우리가 구한 모델과 실제 데이터의 CDF를 각각 구하여 그 차이가 가장 큰 spot을 찾는다
실제 가능한 $x_{min}$ 중 그 spot의 차이를 가장 최소화 할 수 있는 값을 찾아 그것을 $x_{min}$ 으로 사용한다.

D = max|F(x|\gamma,x_{min})-F_{exp}(x)|

x^*_{min} = argmin_{x_{min}}D

실제 계산

먼저 $x_{min}$ 의 후보들을 정한다
이 $x_{min}$ 을 이용하여 $\gamma$ 를 추정한다
이 $x_{min}$ 과 $\gamma$ 의 쌍을 이용하여 KS test에서의 D를 각각 구하고 이 중 가장 작은 값의 쌍을 채택한다

두 개의 파라미터는 서로 의존적이므로 반복적인 계산을 통해 추정할 수 있다.

마무리

수학적으로 접근하는 Power-law distribution은 끝이 없는 것 같고 실제로 이보다 훨씬 방대한 양의 내용을 다루고 있는 것 같다.
하지만 그만큼 유의미한 정보를 가지고 있는 분포임은 확실하고 만약 이를 우리 실생활에 적용할 수 있는 사례들에 대해서는 굉장히 많은 정보를 가져다 줄 것으로 보인다