다익스트라 알고리즘
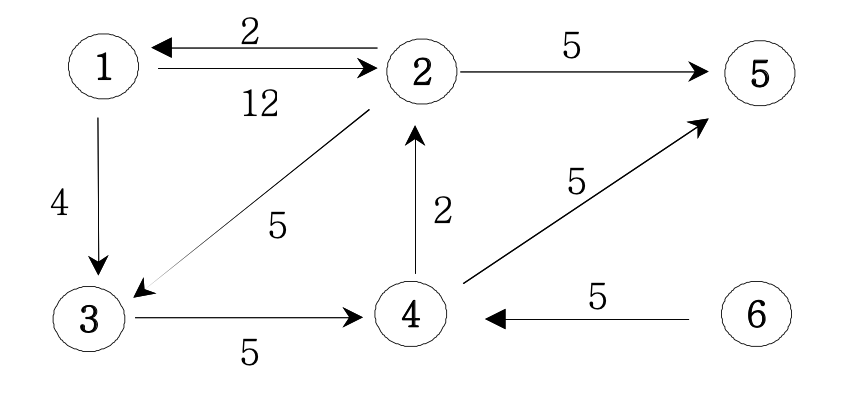
아래의 가중치 방향그래프에서 1번 정점에서 모든 정점으로의 최소 거리비용을 출력하는 프로 그램을 작성하세요. (경로가 없으면 Impossible를 출력한다)
입력 설명
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연 결정보와 거리비용이 주어진다.
출력 설명
1번 정점에서 각 정점으로 가는 최소비용을 2번 정점부터 차례대로 출력하세요.
입력
6 9
1 2 12
1 3 4
2 1 2
2 3 5
2 5 5
3 4 5
4 2 2
4 5 5
6 4 5
출력
2:11
3:4
4:9
5:14
6 : impossible
구현 코드
public class 다익스트라알고리즘 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();//정점의 수
int m = in.nextInt();//간선의 수
ArrayList<ArrayList<Edge>> graph = new ArrayList<>();
for(int i=0;i<=n;i++){
graph.add(new ArrayList<>());
}
for(int i=0;i<m;i++){
graph.get(in.nextInt()).add(new Edge(in.nextInt(),in.nextInt()));
}
int[] dis = new int[n+1];
Arrays.fill(dis, Integer.MAX_VALUE);
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.offer(new Edge(1,0));
dis[1] = 0;
while(!pq.isEmpty()){
Edge tmp = pq.poll();
int now = tmp.node;
int nowCost = tmp.cost;
if(nowCost>dis[now]) continue;
for (Edge ob : graph.get(now)){
if(dis[ob.node]>nowCost+ob.cost){ //시작노드에서 바로가는 길보다 현재노드 거쳐서 가는 길의 비용이 더 작을 경우
dis[ob.node] = nowCost + ob.cost;
pq.offer(new Edge(ob.node,nowCost+ob.cost));
}
}
}
for(int i=2;i<=n;i++){
if(dis[i]!=Integer.MAX_VALUE) System.out.println(i+" : "+dis[i]);
else System.out.println(i+" : impossible");
}
}
static class Edge implements Comparable<Edge>{
@Override
public int compareTo(Edge o){
return this.cost - o.cost;
}
public Edge(int node, int cost) {
this.node = node;
this.cost = cost;
}
int node;
int cost;
}
}Dijkstra란?
다익스트라 알고리즘은 음의 가중치가 없는 그래프의 한 노드에서 각 모든 노드까지의 최단거리를 구하는 알고리즘이다. 기본적으로 Greedy와 DP 기법을 사용한 알고리즘이다. PriorityQueue를 사용하면 O(ElogV)까지 시간복잡도를 줄일 수 있다.
[방식]
1. 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택(Greedy)
2. 해당 노드로부터 갈 수 있는 노드들의 비용을 갱신(DP)
[구현 방법]
1. Edge class( node1, cost : node1로 가는 간선의 비용이 cost) 선언
1. 각 정점의 이웃 간선 정보를 담는 ArrayList 선언
2. 정점들의 ArrayList를 담는 ArrayList인 graph 선언
3. 각 정점까지의 거리 비용을 담는 dis 배열 선언 -> Integer.MAX_VALUE로 fill (무한대값으로 채운다고 생각)
4. PriorityQueue 선언 (비용이 최소인 간선 부터 빼는 queue)
5. 시작 정점 정보 add
6. while(!pq.isEmpty())
하나씩 빼면서 if(시작 정점에서 각 정점까지 바로 가는 길 > 현재 정점 거쳐서 각 정점까지 가는 길)
dis 정보 업데이트(최소 비용으로)
pq.add
