[LeetCode-Medium]64. Minimun Path Sum - JS

문제

양수로 이루어진 m x n 그리드를 인자로 드립니다.
상단 왼쪽에서 시작하여, 하단 오른쪽까지 가는 길의 요소를 다 더했을 때,
가장 작은 합을 찾아서 return 해주세요.

한 지점에서 우측이나 아래로만 이동할 수 있습니다.

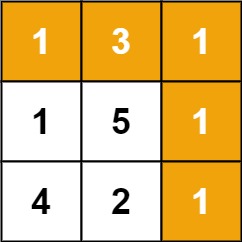
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.

Input: grid = [[1,2,3],[4,5,6]]
Output: 12

내 방법(성공!)

DFS 방식으로 풀어야 할 것 같았다. 재귀이면서 갈 수 있는 레벨이 정해져 있으니까.

처음에는 x가 배열의 끝으로 갈 때 (x === m-1) 이 부분을 else if로 하지 않고 if로만 했더니 아래부분까지 돌면서 에러가 났다.
이 에러 찾는데 한참 걸렸다 .. !

2시간반 정도 걸렸다.

const minPathSum = grid => {
  let m = grid.length;
  let n = grid[0].length;
  let min_sum = 10000;

  function D(L, x, y, t_sum) {
    if (L >= (m+n-2)) {
      if (min_sum > t_sum) {
        min_sum = t_sum;
        return
      }
      return
    } else if (x === m-1) {
      D(L+1, x, y+1, t_sum + grid[x][y+1])    
    } else if (y === n-1) {
      D(L+1, x+1, y, t_sum + grid[x+1][y])
    } else {
      D(L+1, x+1, y, t_sum+grid[x+1][y]);
      D(L+1, x, y+1, t_sum+grid[x][y+1])
    }
    return min_sum
  }

  return D(0,0,0, grid[0][0])
};

고수의 방법

var minPathSum = function(grid) {
	// Get the two dimensions of the grid
    const n = grid.length;
    const m = grid[0].length;
    
	// Calculate the distance travelled within the first column
	// This is because each square depends on the one above
	// And the one to the left. However there is nothing left
	// of the first column so we can calculate it by adding
	// the current square to the square above it
    for(let i=1; i<n; i++) {
        grid[i][0] += grid[i-1][0];
    }
    
	// The same goes for the first row. There is nothing above the 
	// first row. So we just calculate the distance by what is to the left
	// of it
    for(let j=1; j<m; j++) {
        grid[0][j] += grid[0][j-1];
    }
    
	// Start one row and one column in because we've precomputed
	// those above
    for(let i=1; i<n; i++) {
        for(let j=1; j<m; j++) {
			// The distance to the grid at i,j is equal to itself plus the minimum
			// of the two grid spaces (one above, one to the left)
            grid[i][j] += Math.min(grid[i-1][j], grid[i][j-1]);
        }
    }
    
	// Return the distance bottom right corner
    return grid[n-1][m-1];
};

첫번째 두번째 for문

[0,0]에서 행, 열로 가면서 그 배열의 수의 합을 누적시킨다.
아래 output 으로 바뀐다.
아래 배열에서 [1,1], [2,1]은 변함이 없다.

// input
[[1,2],
 [1,3],
 [1,4]]

// output
[[1,3],
 [2,3],
 [3,4]]

세번째 for문

[1,1]에서 위와 왼쪽 중 작은 수를 택해서 자신과 합한다.
[2,1]에서 위와 왼쪽 중 작은 수를 택해서 자신과 합한다.
최종배열의 모양은 이렇다.

[[1,3],
 [2,5],
 [3,7]]