비선형 자료구조

비선형구조(= 트리, 그래프)의 각 노드(정점)를 중복되지 않게 "전부" 방문하는 것을 의미함.

선형구조와 다르게 선후 연결 관계를 알 수 없다.
=> 특별한 방법이 필요하다

두 가지 방법
1. 깊이 우선 탐색 (Depth First Search, DFS)
2. 너비 우선 탐색 (Breadth First Search, BFS)

DFS (Depth First Search)

• 루트 노드에서 출발하여 한 방향으로 갈 수 있는 곳까지 "깊이 탐색"을 하고, 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 노드로 되돌아와서 다른 방향의 노드로 탐색을 계속 반복하여 결국 모든 노드를 방문하는 순회 방법

• 가장 마지막에 만났던 갈림길의 노드로 되돌아 가서 다시 깊이 우석 탐색을 반복 => 재귀 or 스택 으로 구현 가능

간단한 트리 DFS 코드

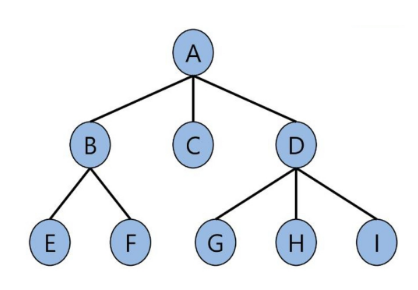
tree = {'A': ['B', 'C', 'D'],
		'B': ['E', 'F'],
        'D': ['G', 'H', 'I']}
        
def dfs(tree, node):
	print(node) # 방문한 노드 출력
    
    if node not in tree: # 자식 노드가 없으면 종료
    	return
        
    for child in tree[node]: # 자식 노드들을 순서대로 다시 탐색
    	dfs(tree, child)
        
dfs(tree, 'A')

DFS - 그래프

시작 정점에서 출발하여 한 방향으로 갈 수 있는 곳까지 "깊이 탐색"을 진행하고, 더 이상 갈 곳이 없다면 가장 마지막 갈림길 간선이 있는 정점에서 다시 "깊이 탐색"을 진행하는 흐름은 같음.

하지만 자식 노드라는 관계가 없기 때문에 "방문여부"를 체크한다.

간단한 그래프 DFS 코드

N = 5  # 정점의 수
# 인접 행렬로 그래프 표현
adj_matrix = [
	[0, 1, 1, 0, 0]
    [1, 0, 0, 1, 1],
    [1, 0, 0, 0, 1],
    [0, 1, 0, 0, 1],
    [0, 1, 1, 1, 0]
]
visited = [False] * N

def dfs(current, adj_matix, visited):
	visited[current] = True
    
    for i in range(len(adj_matrix)):
    	# 현재 정점과 연결되어 있고, 아직 방문하지 않은 정점이라면
    	if adj_matrix[current][i] and not visited[i]:
        	dfs(i, adj_matrix, visited)

# 연결되어 있지 않은 정점을 위해 모든 정점에 대해 dfs 실행
for i in range(N):
	if visited[i]:
    	continue
    
    dfs(0, adj_matrix, visited)