트리와 그래프

유승현·2025년 3월 19일

BST 그래프 알고리즘 트리

Algorithm

목록 보기

3/6

트리(Tree)

비선형 구조
원소들 간에 1:N 관계를 가지는 자료구조
원소들 간에 "계층관계"를 가지는 계층형 자료구조
상위 원소에서 하위 원소로 내려가면서 확장되는 트리(나무)모양의 구조

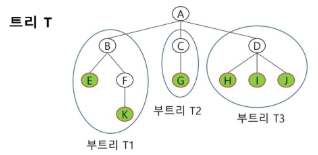
트리의 정의

한 개 이상의 노드로 이루어진 유한 집합
노드 중 최상위 노드를 루트(root)라 한다.
나머지 노드들은 n(>= 0)개의 분리 집합 T1, T2, ..., Tn으로 분리될 수 있다.
분리 집합 각각은 하나의 트리가 되며(재귀적 정의) 루트의 부 트리(subtree)라 한다.

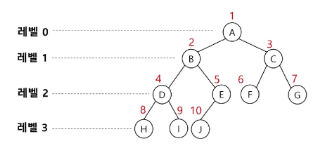
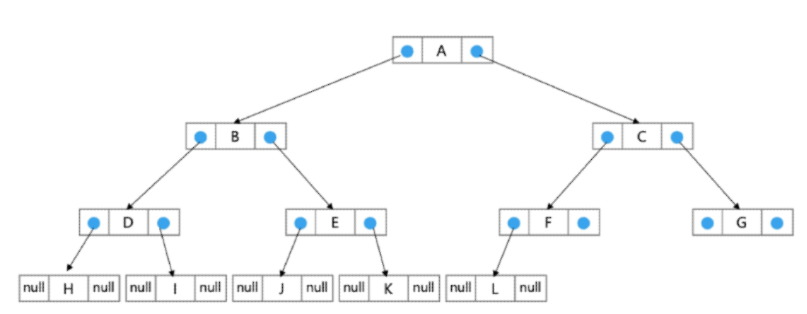
트리 용어

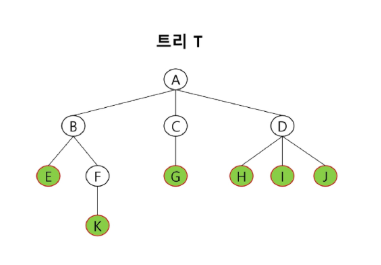
노드 (node)
- 티리의 원소를 의미함
- A, B, C, ...
간선 (edge)
- 노드와 노드를 연결하는 선
- 부모 노드와 자식 노드를 연결
루트 노드 (root node)
- 트리의 시작 노드인 최상위 노드
- 트리 T의 루트 노드 = A
형제 노드 (sibling node)
- 같은 부모 노드의 자식 노드들
- B, C, D는 형제 노드
조상 노드 (ancestor node)
- 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드들
- K의 조상 노드: F, B, A
서브 트리 (subtree)
- 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
자손 노드 (descendant node)
- 서브 트리에 있는 하위 레벨의 노드들
- B의 자손 노드: E, F, K
차수 (degree)
- 노드의 차수
- 노드에 연결된 자식 노드 수
- B의 차수 = 2, C의 차수 = 1
- 트리의 차수
- 트리에 있는 노드의 차수 중에서 가장 큰 값
- 트리 T의 차수 = 3
- 단말 노드 (leaf node)
- 차수가 0인 노드. 즉, 자식 노드가 없는 노드

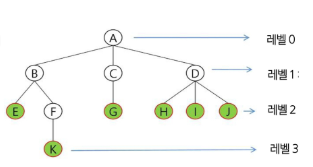
레벨
- 루트에서 노드까지의 거리
- 로트 노드의 레벨은 0, 자식 노드의 레벨은 부모 레벨 + 1
높이
- 루트 노드엠서 가장 먼 리프 노트까지의 간선 수
- 트리의 높이는 최대 레벨 (트리 T의 높이 = 3)

이진 트리(Binary Tree)

차수가 2인 트리
각 노드가 자식 노드를 최대 2개 까지 가질 수 있는 트리 (왼쪽, 오른쪽 자식 노드)

ex)

이진 트리 특성

레벨 i에서의 노드의 최대 개수는 2^i개
높이가 h인 이진 트리가 가질 수 있는 노드의 최소 개수는 (h+1)개가 되며, 최대 개수는 (2^{h+1}-1)개가 된다.

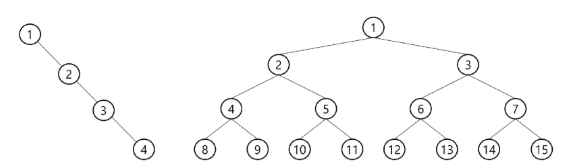
포화 이진 트리(Perfect Binary Tree)

모든 레벨에 노드가 포화 상태로 차 있는 이진 트리
높이가 h일 때, 최대 노드 개수인 (2^{h+1}-1)의 노드를 가진 이진 트리
- 높이가 3일 때 2^{3+1}-1 = 15개의 노드
루트를 1번으로 하여 2^{h+1}-1까지 정해진 위치에 대한 노드 번호를 가짐

이렇게 꽉 찬 이진 트리를 의미함

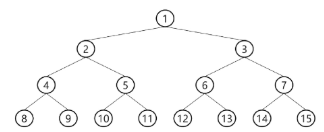
완전 이진 트리(Complete Binary Tree)

높이가 h이고 노드 수가 n일 때 (단, h+1 <= n < 2^{h+1}-1), 포화 이진 트리의 노드 번호 1번부터 n번까지 빈 자리가 없는 이진 트리

이렇게 왼쪽부터 오른쪽으로 하나씩 채워져 나가는 트리

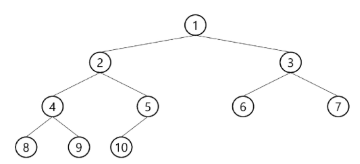
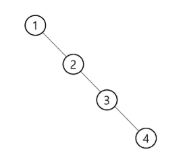
편향 이진 트리(Skewed Binary Tree)

높이 h에 대한 최소 개수의 노드를 가지면서 한쪽 방향의 자식 노드 만을 가진 이진 트리
- 왼쪽 편향 이진 트리

- 오른쪽 편향 이진 트리

리스트를 이용한 이진 트리

파이썬에서는 리스트를 이용하여 이진 트리를 표현할 수 있다.

우선 이진 트리를 숫자로 표현하면 다음과 같다.

여기서 규칙을 찾을 수 있다.
바로 왼쪽 자식 노드는 (부모 노드 x 2), 오른쪽 자식 노드는 (부모 노드 x 2 + 1) 이다.
이를 활용하여 노드를 표현하면 다음과 같다.

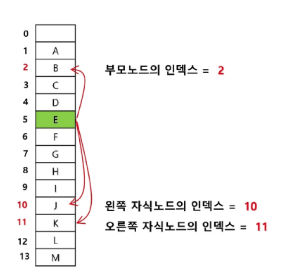
이렇게 인덱스를 활용하여 노드를 표현하고 이를 활용해 해당 노드의 부모 노드와 자식 노드들을 찾을 수 있다!

ex) 이를 활용한 이진 트리 구현

class BinaryTree:
	def __init__(self):
    	self.tree = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L']
    
    def insert(self, value):
    	self.tree.append(value)
    
    def get_node(self, index):
    	if index < len(self.tree):
        	return self.tree[index]
        return None
        
	def set_node(self, index, value):
    	while len(self,tree) < index:
        	self.tree.append(None)
        self.tree[index] = value
        
	def get_left_child(self, index):
    	left_index = 2 * index
        if left_index < len(self.tree):
        	return self.tree[left_index]
        return None
        
	def get_right_child(self, index):
    	right_index = 2 * index + 1
        if right_index < len(self.tree):
        	return self.tree[right_index]
        return None
        
	def get_parent(self, index):
    	if index = 0:
        	return None
        parent_index = index // 2
        return self.tree[parent_index]

리스트를 이용한 이진 트리 표현의 단점

편향 이진 트리의 경우에 사용하지 않는 리스트 원소에 대한 메모리 낭비 발생
트리 중간에 새로운 노드를 삽입하거나 기존의 노드를 삭제할 경우 리스트의 크기 변경이 어려워 비효율적

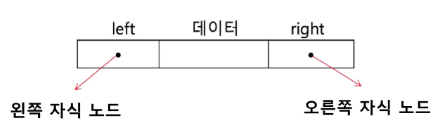
연결 리스트를 이용한 이진 트리 표현

리스트를 이용한 이진 트리의 표현의 단점을 보완하기 위해 연결 리스트를 이용하여 트리를 표현할 수 있다.
이진 트리의 모든 노드는 최대 2개의 자식 노드를 가지므로 일정한 구조의 이중 연결 리스트 노드를 사용하여 구현

이진 트리 순회(traversal)

트리의 노드들을 체계적으로 방문하는 것.
3가지 기본적인 순회 방법
1. 전위 순회(Preorder Traversal) : VLR 순서로 순회
1. 중위 순회(Inorder Traversal) : LVR 순서로 순회
2. 후위 순회(Postorder Traversal) : LRV 순서로 순회

해당 구현들은 재귀의 순서만 바꾸면 쉽게 구현할 수 있다.

ex) 전위 순회 구현

class TreeNode:
	def __init__(self, key):
    	self.left = None
        self.right = None
        self.val = key
        
def preorder_traversal(root):
	if root:
    	print(root.val)
        preorder_traversal(root.left)
        preorder_traversal(root.right)

ex) 중위 순회 구현

class TreeNode:
	def __init__(self, key):
    	self.left = None
        self.right = None
        self.val = key
        
def inorder_traversal(root):
	if root:
    	inorder_traversal(root.left)
    	print(root.val)
        inorder_traversal(root.right)

ex) 후위 순회 구현

class TreeNode:
	def __init__(self, key):
    	self.left = None
        self.right = None
        self.val = key
        
def postorder_traversal(root):
	if root:
    	postorder_traversal(root.left)
    	postorder_traversal(root.right)
        print(root.val)

수식 트리(Expression Tree)

수식을 표현하는 이진 트리
수식 이진 트리(Expression binary Tree)라고 부르기도 함
연산자는 루트 노드이거나 가지 노드
피연산자는 모두 잎 노드

동일한 트리에 대해 세가지 순회 방법에 따른 계산 방법

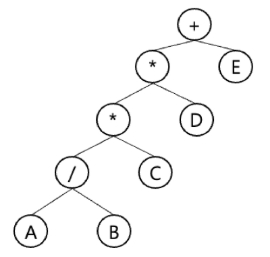
전위 순회 : + * * / A B C D E
중위 순회 : A / B * C * D + E
후위 순회 : A B / C * D * E +

그래프

그래프 유형과 표현

아이템(사물 또는 추상적 개념)들과 이들 사이의 연결 관계를 표현한다.
정점(Vertex): 그래프의 구성요소로 하나의 연결점
간선(Edge): 두 정점을 연결하는 선
차수(Degree): 정점에 연결된 간선의 수
그래프 = 정점(Vertex)들의 집합과 이들을 연결하는 간선(Edge)들의 집합으로 구성된 자료 구조
```
	- V: 정점의 개수, E: 그래프에 포함된 간선의 개수
```
- V 개의 정점을 가지는 그래프는 최대 V * (V - 1) / 2 간선이 개수
선형 자료구조나 트리 자료구조로 표현하기 어려운 M:N 관계를 가지는 원소들을 표현하기에 용이하다.

그래프 유형

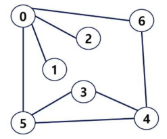
무방향 그래프(Undirected Graph)

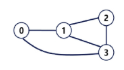
방향 그래프(Directed Graph)

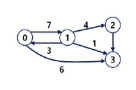
가중치 그래프(Weighted Graph)

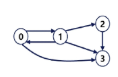
사이클 없는 방향 그래프(DAG, Directed Acyclic Graph)

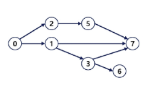
트리(Tree)

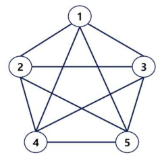
완전 그래프
정점들에 대해 가능한 모든 간선들을 가진 그래프

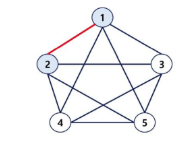
부분 그래프
원래 그래프에서 일부의 정점이나 간선을 제외한 그래프

인접 정점

인접(Adjacency)

두 개의 정점에 간선이 존재 (연결됨)하면 서로 인접해 있다고 한다.
완전 그래프에 속한 임의의 두 정점들은 서로 인접해 있다.
두 정점 1과 2는 서로 인접해 있다.

그래프 경로

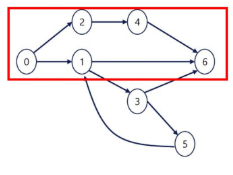
경로 : 어떤 정점 A에서 시작하여 다른 정점 B로 끝나는 순회로 두 정점 사이를 잇는 간선들을 순서대로 나열할 것.

같은 정점을 거치지 않은 간선들의 sequence
어떤 정점에서 다른 정점으로 가는 경로는 여러가지일 수 있다.
0 - 6의 경로 예시
- 정점들: 0 - 2 - 4 - 6
- 간선들: (0, 2), (2, 4), (4, 6)

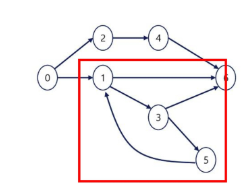
사이클 : 경로의 시작 정점과 끝 정점이 같음 = 시작한 정점에서 끝나는 경로

1 - 3 - 5 - 1

그래프를 표현하는 세가지 방법

인접 행렬(Adjacent Matrix): V * V 크기의 2차원 배열을 이요해서 간선 정보를 저장
인접 리스트(Adjacent List): 각 정점마다 다른 정점으로 나가는 간선의 정보를 저장
간선 리스트(Edge List): 간선의 정보를 객체로 표현하여 리스트에 저장

1. 인접 행렬

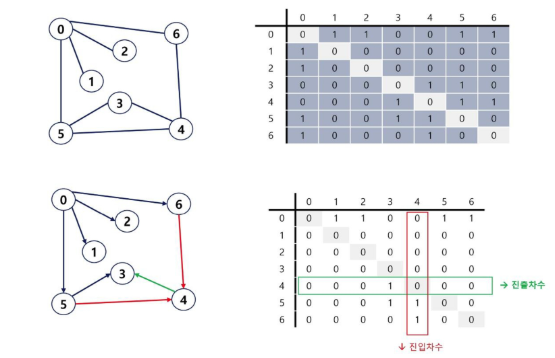
이렇게 무향 그래프, 유향 그래프인지에 따라 행렬의 형태가 달라진다.
무향 = 대칭 행렬
유향 = 비대칭 행렬

장점

두 정점 사이의 간선이 있는지 확인하는 연산이 O(1)로 빠름

구현이 단순

정적 그래프에 적합.(정적 그래프: 정점과 간선의 수가 변하지 않음)

단점

많은 메모리를 차지함 = O(V^2)

간선의 수를 확인하거나 인접한 정점을 나열하는 연산이 느림

사용하기 좋은 상황

Dense Graph(밀집 그래프)에 적합

두 정점 사이에 간선이 있는지 빠르게 확인해야 하는 경우

2. 인접 리스트

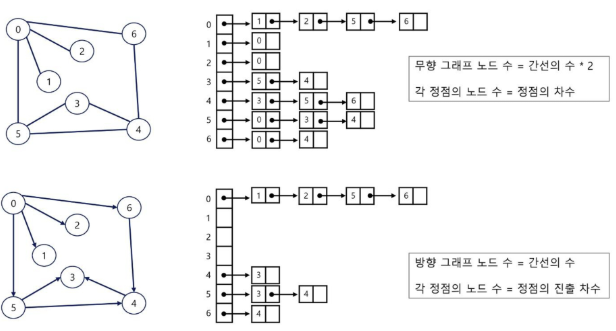
이렇게 해당 정점과 연결된 정점을 표시. 무향이면 그 표시가 2배가 됨.

장점

필요한 공간만 사용하므로 공간 복잡도 O(V + E)

인접한 정점을 나열하는 연산이 빠름

단점

두 정점 사이에 간선이 있는지 확인하는 연산이 느림 = O(V)

Linked List로 구현이 복잡

사용하기 좋은 상황

Sparse Graph(희소 그래프)에 적합

그래프가 동적으로 변하는 경우 (정점과 간선이 자주 추가/삭제 되는 경우)

인접한 정점을 자주 순회해야 하는 경우

3. 간선 리스트

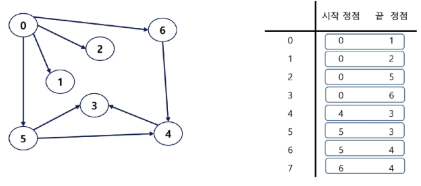
두 정점에 대한 간선 그 자체를 객체로 표현하여 리스트로 저장

장점

필요한 간선만 저장하므로 공간 복잡도 O(E)

간선을 직접 다루는 연산에 효율적

단점

두 정점 사이에 간선이 있는 지 확인하는 연산이 느림 = O(E)

특정 정점에 인접한 정점을 찾는 연산이 느림 = O(E)

사용하기 좋은 상황

간선 중심 연산을 자주 수행해야 하는 경우. ex) MST

BST

BST (Binary Search Tree)

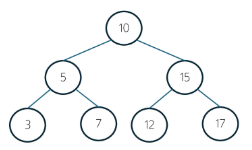
정의

데이터의 저장, 검색, 삽입, 삭제를 효율적으로 처리하기 위한 자료구조

특징

각 노드가 최대 2개의 자식을 가짐
데이터를 정렬된 형태로 저장하여 탐색/삽입/삭제를 효율적으로 수행

구조

이진 트리의 특성을 가지지만 추가로 다음과 같은 속성을 가짐(순서 속성)
- 왼쪽 자식 노드의 키 값이 부모 노드의 키 값보다 작다.
- 오른쪽 자식 노드의 키 값이 부모 노드의 키 값보다 크다.

장점

배열이나 Linked List와 달라, 삽입/삭제 후에도 데이터가 정렬된 상태를 유지

데이터가 균형있게 분포되어 있을 때 평균적으로 탐색/삽입/삭제 연산의 시간 복잡도가 O(logN)

동적으로 크기를 조절할 수 있어, 크기가 고정된 배열에 비해 유연성이 높음

단점

트리가 한쪽으로 치우치면 (즉, 균형이 맞지 않으면) 최악의 경우, 시간 복잡도가 O(n)이 될 수 있음

각 노드의 두 개의 자식 포인터를 저장해야 하므로, 큰 데이터 집합의 경우 메모리 오버헤드가 발생할 수 있음

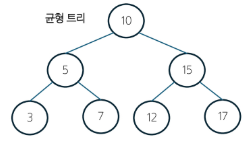
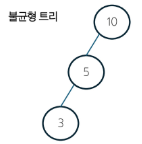
BST 속성

높이

특정 노드에서 가장 깊은 리프 노드까지의 경로에 있는 간선의 개수
트리의 높이는 루트 노드의 높이와 동일
리프 노드의 높이는 0
균형잡힌 트리의 높이는 O(ogN), 불균형한 트리의 높이는 O(N)이다.

깊이

루트 노드에서 해당 노드까지의 경로에 있는 간선의 수
루트 노드의 높이는 0

BST 주요 연산

탐색

루트 노드부터 탐색을 시작하며, 현재 노드값과 찾고자 하는 키를 비교, 그 차에 따라 왼쪽 또는 오른쪽으로 이동.
이를 반복하다 현재 노드값과 찾고자 하는 값이 같으면 탐색 종료

class Node:
	def __init__(self, key):
    	self.key = key
        self.left = None
        self.right = None
        
class BST:
	def __init__(self):
    	self.root = None
    
    def search(self, key):
    	return self._search(self.root, key)
        
    def _search(self, node, key):
    	if node is None or node.key == key:
        	return node
        if key < node.key:
        	return self._search(node.left,key)
        return self._search(node.right, key)

삽입

새로운 노드를 삽입해도 BST의 특징인 "자식노드는 최대 2개"를 유지하면서 삽입할 위치를 찾기위해 루트부터 적절한 위치까지 내려감.
트리의 순서 속성을 유지하기 위해서 새로운 노드는 리프 노드로 삽입

class BST:
	def insert(self, key):
    	if self.root is None:
        	self.root = Node(key)
        else:
        	self._insert(self.root, key)
            
    def _insert(self, node, key):
    	if key < node.key:
        	if node.left is None:
            	node.left = Node(key)
            else:
            	self._insert(node.left, key)
            
        else:
        	if node.right is None:
            	node.right = Node(key)
            else:
    			self._insert(node.right, key)

삭제

삭제하려는 노드의 위치와 자식 노드의 유무에 따라 세 가지 경우로 나눠서 처리
1. 삭제할 노드가 리프 노드인 경우 -> 단순히 제거하면 됨

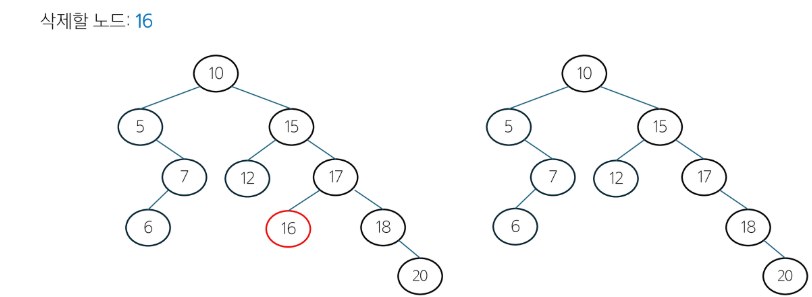
삭제할 노드가 한 개의 자식 노드를 가질 경우 -> 삭제할 노드의 자식노드를 부모 노드에 연결
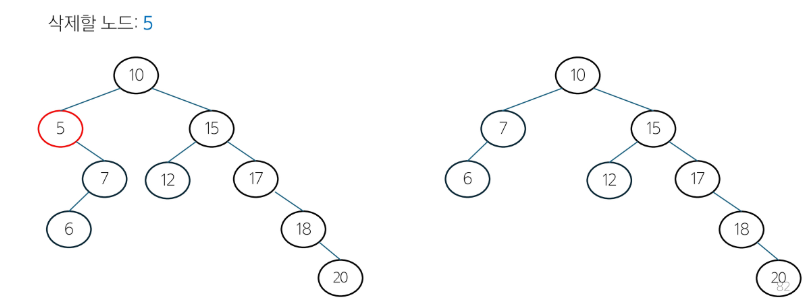
삭제할 노드가 두 개의 자식 노드를 가질 경우 -> 중위 후속자 또는 중위 전임자 찾기

중위 후속자 : 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값 (일반적으로 사용)
중위 전임자 : 삭제할 노드의 왼쪽 서브 틀에서 가장 큰 값
BST 구조를 유지하기 위해서 삭제할 노드와 가장 가까운 값을 찾는 것.

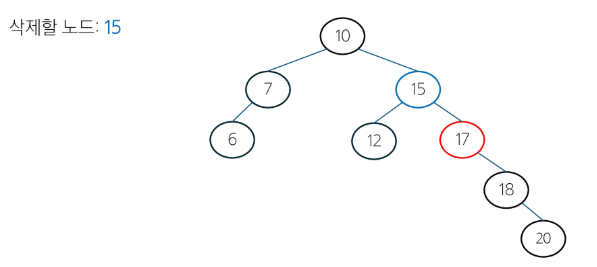
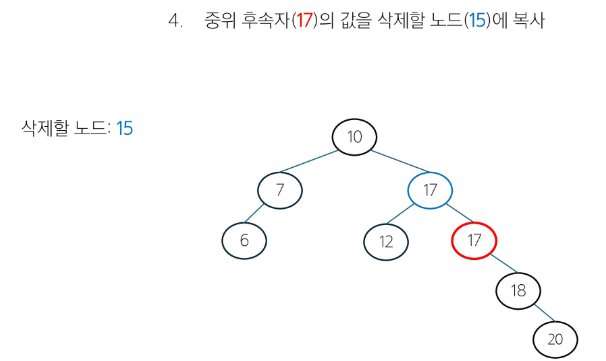
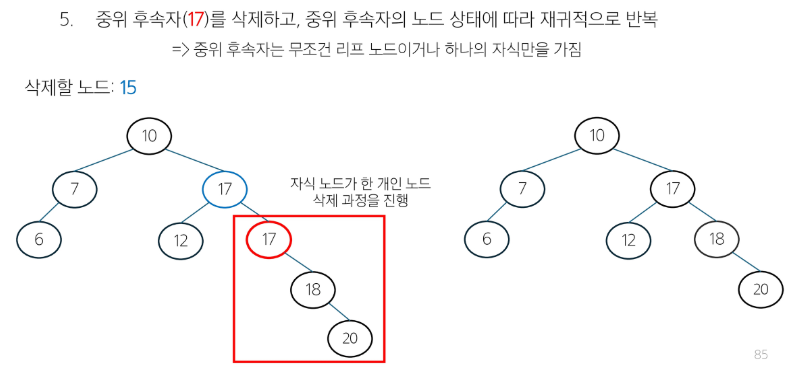
class BST:
	def delete(self, key):
    	self.root = self._delete(self.root, key)
        
    def _delete(self, node, key):
    	if node is None:
        	return node
        
        if key < node.key:
        	node.left = self._delete(node.left, key)
        elif key > node.key:
        	node.right = self._delete(node.right, key)
        else:
        	if node.left is None:
            	return node.right
            elif node.right is None:
            	return node.left
                
            temp = self._minValueNode(node.right)
            node.key = temp.key
            node.right = self._delete(node.right, temp.key)
            
        return node
        
    def _minValueNode(self, node):
    	current = node
        while current.left is not None:
        	current = current.left
        return current

BST의 균형과 불균형

BST의 구조는 삽입되는 데이터의 순서에 따라 결정되기 때문에 특정 패턴으로 삽입되는 경우 불균형이 발생
불균형한 BST의 문제점
- 검색/삽입/삭제 연산의 시간복잡도가 O(N)이 됨. (균형 잡힌 BST의 경우 O(logN))
- 트리의 높이가 증가하게 되면 많은 메로리 공간이 필요
- 트리의 높이가 증가하게 되면서 깊있는 재귀호출로 인해서 스택 오버플로우가 발생할 수 있음
불균형 문제를 해결할 수 있는 방법은?
- 자가 균형 트리(Self-Balancing Tree): AVL Tree, Red-Black Tree

유승현

커피를 넣으면 코드가 나옵니다.

이전 포스트

스택과 큐

다음 포스트