알고리즘 = 문제를 해결하기 위한 절차나 방법
무엇이 좋은 알고리즘 인가?
- 정확성
- 효율성
- 확장성
- 단순성
가장 중요한건 "정확성"
알고리즘을 평가하는 지표 = 복잡도
- 시간 복잡도 (= 수행 시간)
- 공간 복잡도 (= 메모리 사용량)
시간 복잡도
시간 복잡도는 세 가지 경우가 있다.
1. 최선의 경우 (Best Case)
2. 평균적인 경우 (Average Case)S
3. 최악의 경우 (Worst Case)

우리가 중요하게 생각하는건 "최악의 경우"
복잡도는 점근적 표기를 사용한다.
입력 크기 n에 대한 함수로 표기한다.
빅-오(O) 표기법은 함수 중 가장 큰 영향력을 주는 n에 대한 항만을 표시
만약 O(3n + 2) 라면 O(n)으로 표기
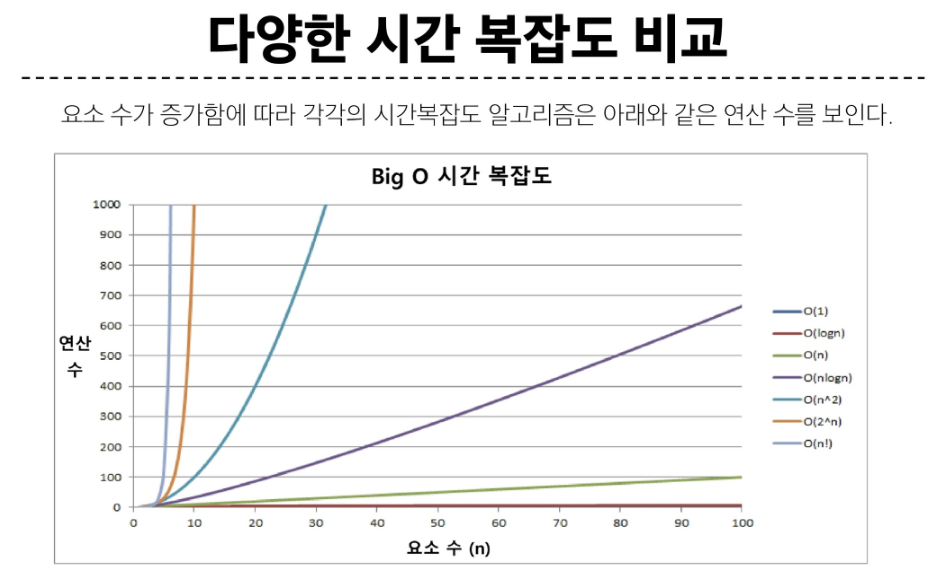
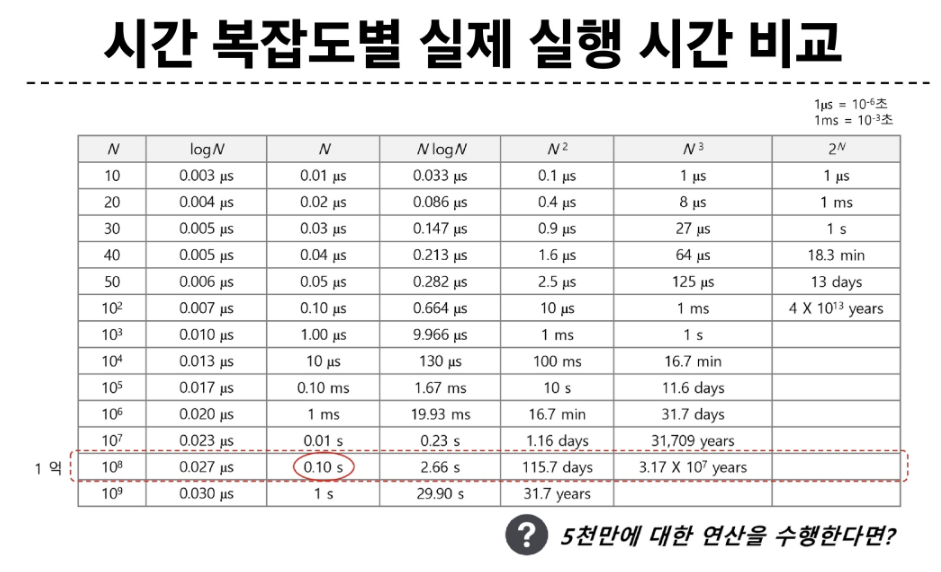
처음 알고리즘을 배울때는 정확도를 최우선으로 고려하고 그 후 빅-오를 통해 효율을 생각하자. 확장성과 단순성이 이후에 고려해도 늦지 않다.
완전 검색
- 정확도를 최우선으로 고려하는 알고리즘
- 문제의 해법으로 생각할 수 있는 모든 경우의 수를 나열해보고 확인하는 기법
- Brute-foce 혹은 generate-and-test 기법이라고도 불린다.
- "Just-do-it"
- force의 의미는 사람(지능)보다는 컴퓨터의 force를 의미한다.
- 대부분의 문제에 적용 가능
- 모든 알고리즘의 시작!!! 매우 중요
완전 검색은 모든 경우의 수를 생성하고 테스트하기 때문에 수행 속도는 느리지만, 해답을 찾아내지 못할 확률이 낮다.
검정 등에서 문제를 풀 때, 우선 완전 검색으로 접근하여 해답을 도출한 후, 성능 개선을 위해 다른 알고리즘을 사용하고 해답을 확인하는 것이 바람직하다.
재귀 함수
- 자기 자신을 호출하는 함수
- 함수 호출은 메모리 구조에서 스택을 사용한다.
- 무분별한 재귀 함수는 성능저하를 발생시킨다.
대표적인 예시 (팩토리얼)
n! = 1 x 2 x 3 x ... x (n-1) x n 이다.
이를 재귀 함수로 표현하면 다음과 같다.
def fact(n):
if n <= 1:
return 1
else:
return n * fact(n-1)이를 그림을 통해 살펴보면 다음과 같다.
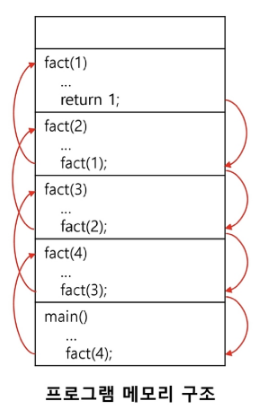
fact(4)에서 fact(3), fact(3)에서 fact(2) 이렇게 자기 자신보다 값이 1 작은 함수를 계속해서 호출하다가 fact(1)이 되면 'return 1'이 되면서 다시 fact(2), fact(3)을 계산하고 최종적으로 시작했던 fact(4)를 return하면서 결과가 반환된다.
추가 예시 (피보나치 수열)
이전의 두 수 합을 다음 항으로 하는 수열을 피보나치 수열이라고 한다.
이를 재귀함수로 구현하면 다음과 같다.
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)가장 시작이 되는 fibonacci(0)과 fibonacci(1)만 return 값을 정의해주면 이후의 값은 재귀적으로 만들어지게 됩니다.
이처럼 재귀함수는 반환이 시작되는 부분을 기본 부분 이라고 하고, 재귀를 쌓는 부분을 유도 부분 이라고 한다.
이를 잘 구분하고 정의하는 것이 재귀함수를 잘 사용하는 첫 걸음이다.
피보나치 수열의 기본 부분과 유도 부분은 다음과 같다.
def fibonacci(n):
if n == 0: # 기본 부분
return 0
elif n == 1: # 기본 부분
return 1
else: # 유도 부분
return fibonacci(n - 1) + fibonacci(n - 2)순열
서로 다른 n개에서 r개를 뽑아 순서대로 나열하는 것. -> 순서가 중요. (표현법 : nPr)
다수의 알고리즘 문제들은 순서화된 요소들의 집합에서 최선의 방법을 찾는 것과 관련이 있다.
이를 반복문을 통해 생성한다면 다음과 같다.
ex) {1, 2, 3}의 모든 순열
for i in range(1, 4):
for j in range(1, 4):
if j != i:
for k in range(1, 4):
if k != i and k != j:
print(i, j, k)이는 n이 커지면 반복문을 그만큼 중첩해야하고, 이를 하나의 함수로 표현하기도 어렵다. 그래서 보통 재귀 호출을 통해 순열을 생성한다.
ex) 재귀 호출을 활용한 {1, 2, 3}의 모든 순열
def perm(selected, remain):
if not remain:
print(selected)
else:
for i in range(len(remain)):
select_i = remain[i]
remain_list = remain[:i] + remain[i + 1:]
perm(selected + [select_i], remain_list)
perm([], [1, 2, 3])재귀 함수가 동작하는 것을 순서대로 따라가면 다음과 같다.
perm([], [1, 2, 3])
-> perm([1], [2, 3]) -> perm([1, 2], [3]) -> perm([1, 2, 3], [])에서 print(1, 2, 3) 실행
-----> perm([1, 3], [2]) -> perm([1, 3, 2], [])에서 print(1, 3, 2) 실행
-> perm([2], [1, 3]) -> perm([2, 1], [3]) -> perm([2, 1, 3], [])에서 print(2, 1, 3)
-----> perm([2, 3], [1]) -> perm([2, 3, 1], [])에서 print(2, 3, 1)
-> perm([3], [1, 2]) -> perm([3, 1], [2]) -> perm([3, 1, 2], [])에서 print(3, 1, 2)
-----> perm([3, 2], [1]) -> perm([3, 2, 1], [])에서 print(3, 2, 1)
이런식으로 진행이 된다.
조합
서로 다른 n개의 원소 중 r개를 순서없이 골라낸 것. (표현법 : nCr)
ex) {1, 2, 3, 4}중 3개를 뽑는 조합을 반복문으로 표현하면?
for i in range(1, 5):
for j in range(i + 1, 5):
for k in range(j+1, 5):
print(i, j, k)순열과 동일하게 r이 증가하면 그만큼 for문이 반복된다. 그래서 보통 재귀 함수를 통해 조합을 생성한다.
ex) 동일한 조합을 재귀 함수로 표현하면?
def comb(arr, r):
result = []
if r == 1:
return [[i] for i in arr]
for i in range(len(arr)):
elem = arr[i]
for rest in comb(arr[i + 1:], r - 1):
result.append([elem] + rest)
return result
print(comb([1, 2, 3, 4], 3))조합의 재귀 함수가 동작하는 것을 순서대로 따라가면 다음과 같다.
comb([1, 2, 3, 4], 3) -> result = [], elem = 1, rest = comb([2, 3, 4], 2)
comb([2, 3, 4], 2) -> result = [], elem = 2, rest = comb([3, 4], 1)
comb([3, 4], 1) -> return [[3], [4]]
comb([2, 3, 4], 2) -> result = [[2, 3], [2, 4]], elem = 3, rest = comb([4], 1)
comb([4], 1) -> return [[4]]
comb([2, 3, 4], 2) -> result = [[2, 3], [2, 4], [3, 4]]
comb([1, 2, 3, 4], 3) -> result = [[2, 3], [2, 4], [3, 4]], elem = 2, rest = comb([3, 4], 2) -> result = [[1, 2, 3], [1, 2, 4], [1, 3, 4]]
comb([3, 4], 2) -> result = [], elem = 3, rest = comb([4], 1)
comb([4], 1) -> return [[4]]
comb([3, 4], 2) -> result = [[3, 4]]
comb([1, 2, 3, 4], 3) -> result = [[1, 2, 3], [1, 2, 4], [1, 3, 4], [2, 3, 4]
중복 순열 & 중복 조합
def comb(arr, r):
result = []
if n == 1:
return [[i] for i in arr]
for i in range(len(arr)):
elem = arr[i]
for rest in comb(arr[i + 1:], r - 1): # 조합
# for rest in comb(arr[:i] + arr[i + 1:] r - 1): # 순열
# for rest in comb(arr, r - 1): # 중복 순열
# for rest in comb(arr[i:], r - 1): # 중복 조합
result.append([elem] + rest)
return result부분 집합(Power Set)
ex) {1, 2, 3}집합의 모든 부분 집합
반목문으로 구현
selected = [0] * 3
for i in range(2):
selected[0] = i
for j in range(2):
selected[1] = j
for m in range(2):
selected[2] = ,
subset = []
for n in range(3):
if selected[n] = 1:
subset.append(n + 1)
print(subset)재귀 함수로 구현
def generate_subset(depth, included):
if depth == len(input_list):
cnt_subset = [input_list[i] for i in range(len(input_list)) if included[i]]
subsets.append(cnt_subset)
return
included[depth] = False
generate_subset(depth + 1, included)
included[depth] = True
generate_subset(depth + 1, included)
input_list = [1, 2, 3]
subsets = []
init_included = [False] * len(input_list)
generate_subset(0, init_included)
print(subsets)Binary Counting 이진법을 활용한 방법
arr = [1, 2, 3]
n = len(arr)
subset_cnt = 2 ** n
subsets = []
for i in range(subset_cnt):
subset = []
for j in range(n):
if i & (1 << j):
subset.append(arr[j])
subsets.append(subset)
print(subsets)
