[Graph] CS224W: Machine learning for Graphs (3)

Lecture 1.3 - Choice of Graph Representation

위 강의는 Stanford CS224W(* 21/W season)를 이해한 내용을 적었습니다.
따라서, 의역이나 오역이 있을 수 있습니다.

강의 요약
그래프 표현의 경우, 다양한 형태와 아래와 같은 요소들을 고려해야 합니다.

• 공간 복잡도: 인접 행렬은 공간 복잡도가 높지만, 인접 리스트와 edge 리스트는 시간 복잡도가 높습니다.
• 시간 복잡도: 인접 행렬은 두 노드 사이의 연결 여부를 확인하는데 시간 복잡도가 낮지만, 인접 리스트와 edge 리스트는 시간 복잡도가 높습니다.
• 정보 손실: 인접 리스트와 edge 리스트는 그래프의 구조 정보를 일부 손실할 수 있습니다.
• 구현 난이도: 인접 행렬과 특징 행렬은 구현하기 쉽지만, 인접 리스트와 간선 리스트는 구현하기 어려울 수 있습니다.

그래프 표현은 그래프의 구조와 속성을 나타내는 방법입니다. 데이터셋이 주어졌을 때, 적절한 그래프 표현을 선택하는 것은 매우 중요합니다.

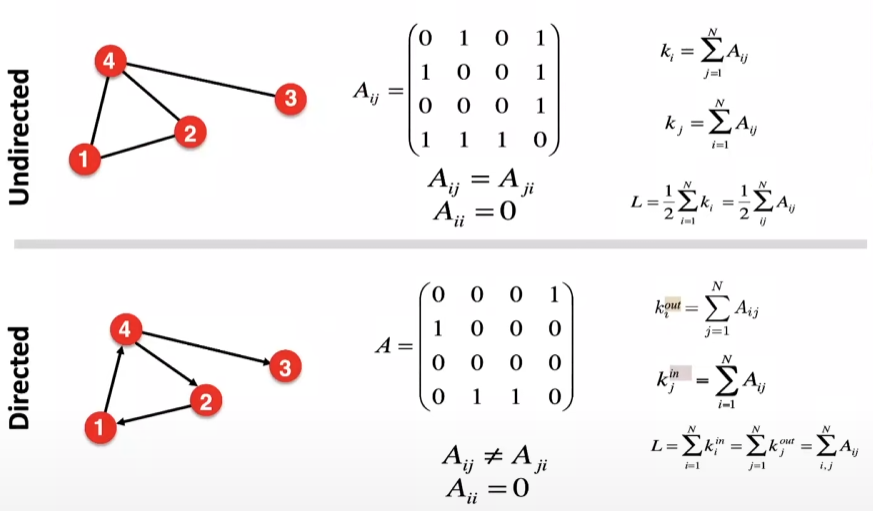
우선 그래프는 아래 이미지처럼 방향성의 유무에 따라 구별할 수 있습니다.

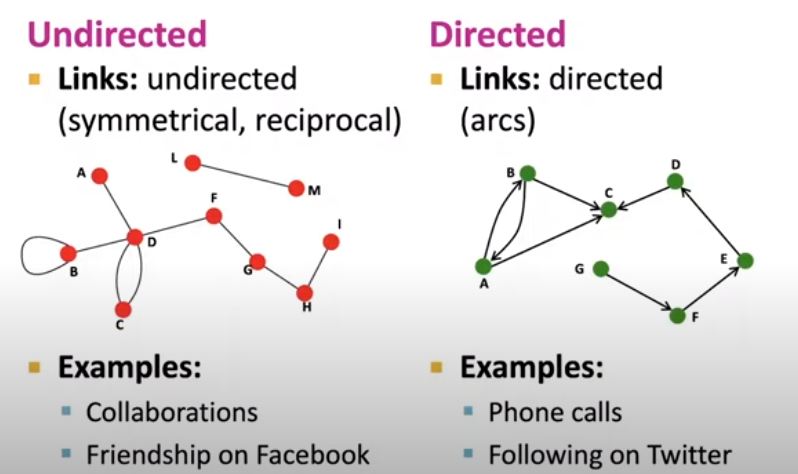
방향성이 없는 그래프는(현재는 유행이 지났지만) Facebook 친구나 싸이월드의 1촌을 예로 들 수 있습니다.
반면, 방향성이 있는 그래프의 경우, 인스타그램의 팔로우/팔로워 관계나, 전화 송/수신 여부를 방향성 그래프(DAG)으로 표현할 수 있습니다.

Node degrees

Node degrees란 특정 노드에서 연결된 edges 개수

• 무방향 그래프는 단순히 주어진 노드에 인접한 가장자리의 수입니다. 평균 노드 차수는 단순히 그래프에 있는 모든 노드 차수에 대한 평균입니다. 이에 대한 공식은 아래와 같으며, 자체 루프 그래프의 경우에도 동일합니다.
  

• 방향성 그래프(DAG): 방향성 그래프에서는 in-degree와 out-degree를 구별합니다. in-degree는 노드를 가리키는 가장자리의 수입니다.
  예를 들어, 아래의 방향성 그래프가 있다고 가정하겠습니다.
  
  수식은 아래와 같습니다. 그래프의 모든 edge가 두 노드를 연결하므로, 모든 노드의 차수의 합은 edge 수의 2배와 같다는 사실에 기반합니다.

  $\displaystyle \bar{k} = <k> = \frac{1}{N}\sum_{i=1}^{N}k_{i} = \frac{2E}{N}$

그래프 표현의 종류

• 인접 행렬: 각 노드가 다른 노드와 어떻게 연결되어 있는지를 나타내는 2차원 배열입니다.
  이 행렬의 크기는 노드의 수에 따라 결정됩니다. 아래 예시입니다.
  
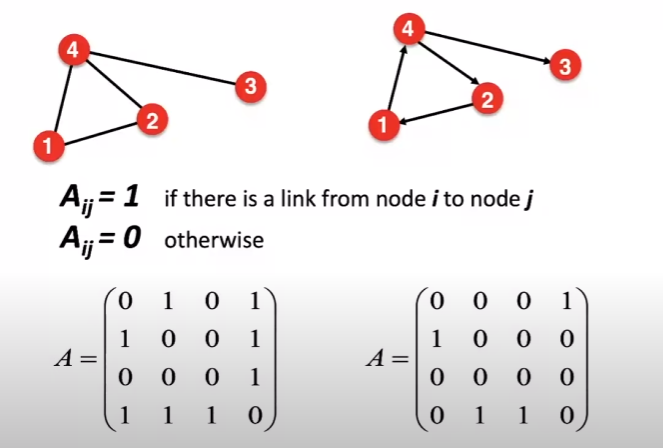
  위 경우는 노드와 edge가 4개이므로, 4x4의 정사각행렬을 생성합니다. 행렬의 각 원소는 두 노드 사이의 연결 여부를 나타내며, 0(연결 x)과 1(연결 o)로 나타낼 수 있습니다. 이 방법은 두 노드 사이의 연결을 쉽게 확인할 수 있지만, 공간 복잡도가 높고, 그래프의 구조 정보를 잘 반영하지 못한다는 단점이 있습니다. 하지만, 행렬곱 연산이 비약적으로 발전한 지금은 해당 단점을 상쇄할 수 있을지도 모르겠네요.
  여기서 실제 그래프(네트워크)의 중요한 결과 중 하나는 네트워크가 매우 희박하다는 것입니다. 이를 희소 행렬이라고 하는데요, 행렬의 대부분의 원소가 0인 행렬을 말합니다.
  대부분의 노드가 서로 연결되어 있지 않은 경우, 해당 그래프의 인접 행렬은 대부분의 원소가 0이 됩니다. 이런 경우를 희소 그래프라고 하며, 이러한 그래프의 인접 행렬은 희소 행렬이 됩니다.
  희소한 인접 행렬은 메모리를 비효율적으로 사용하게 되므로, 이를 보완하기 위해 다양한 데이터 구조(연결 리스트, CSR 등)가 사용된다고 합니다.

• edge 리스트: 그래프의 모든 edge을 목록으로 저장하는 방법입니다. 이 방법은 edge의 수에 따라 공간을 차지합니다.
  
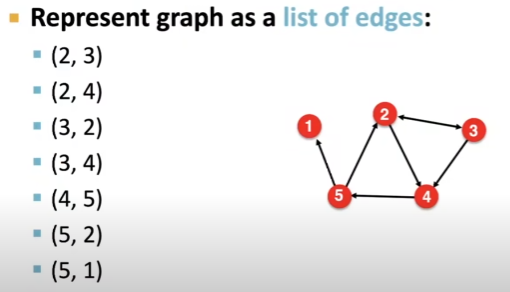
  이전 causalNex를 포스팅했을 때, 많이 보았던 구조네요, 인과 관계를 정의하기 위해 활용할 것 같습니다. 위 개념은 그래프의 구조를 2차원 행렬로 간단하게 표현할 수 있습니다.
  하지만, 문제는 주어진 노드의 차수를 계산하는 것조차 어렵고, 그래프 조작 및 분석을 하기 매우 어렵다고 합니다. 강의 영상에서는 그 이유를 설명해주시지 않았지만, 아마도 차원의 저주 개념과 방향성을 고려한 2차원 표현 방식이 그 이유일 것 같습니다.

• 인접 리스트: edge 리스트 표현 방식보다 나은(?) 개념이라고 합니다. 각 노드가 연결된 다른 노드의 목록을 저장하는 방법입니다. 이 방법은 공간 효율성이 뛰어나므로, 크고 희소 행렬의 네트워크의 경우 작업하기 더 쉽다고 합니다. 또한, 주어진 노드의 모든 이웃을 신속하게 검색할 수 있습니다. 두 노드 사이의 연결 여부를 확인하는데 시간이 걸릴 수 있습니다.
  

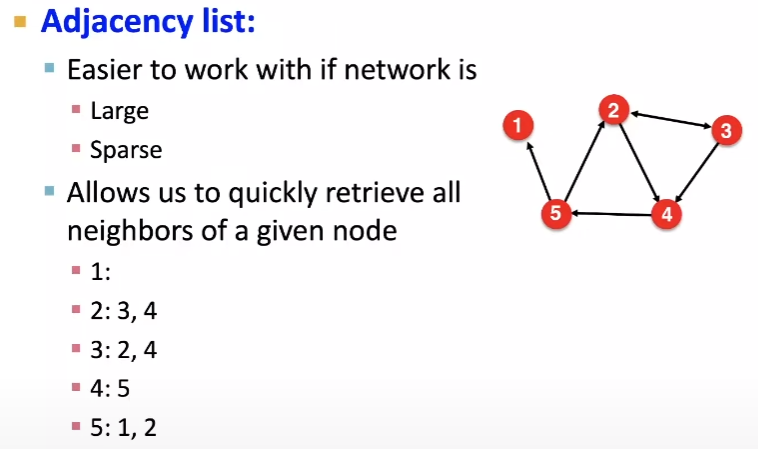
• 특징(속성) 행렬: 각 노드의 속성을 나타낼 수 있습니다. 전체 그래프에는 및 인접 행렬에서 속성을 나타낼 수 있습니다. 예를 들어, Facebook이나 싸이월드의 일촌 관계를 넘어, 두 노드간 상호 교류의 정도에 따라 가중치를 부여할 수 있는 개념인 것 같습니다. 꼭 가중치가 아니더라도, 랭킹, 관계의 호/불호 등의 정보를 나타낼 수 있습니다. 아래 이미지처럼 인접 행렬에서의 가중치를 나타낸 예시입니다.
  
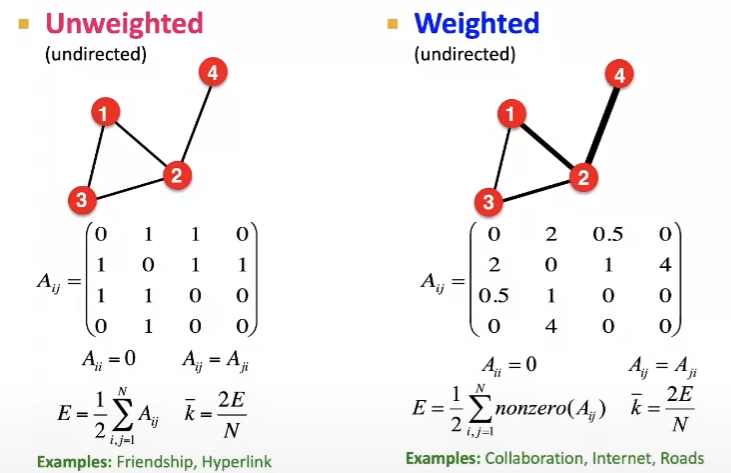
  또한, 아래와 같이, Multigraph나 self-edges 형태로 나타낼 수 있습니다. multigraph의 경우, 가중치 속성으로 나타낼 수도 있지만, 다양한 관계도를 표현하는 등의 상황에서 multigraph를 사용할 수 있습니다.
  
  

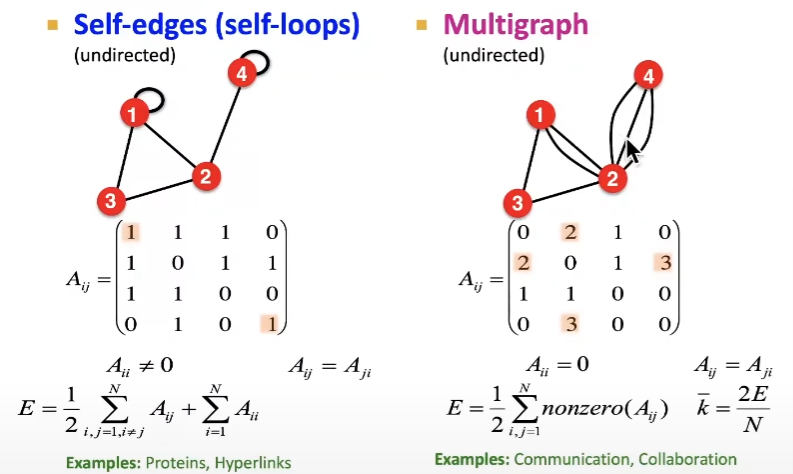
Connectivity: 연결성

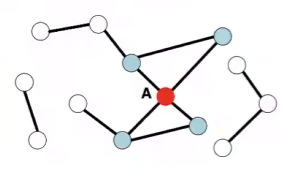
모든 노드들이 서로 연결되어있지 않으며, 보통은 특정 노드끼리 군집을 이루어 연결됩니다. 우선 아래 이미지를 보겠습니다.

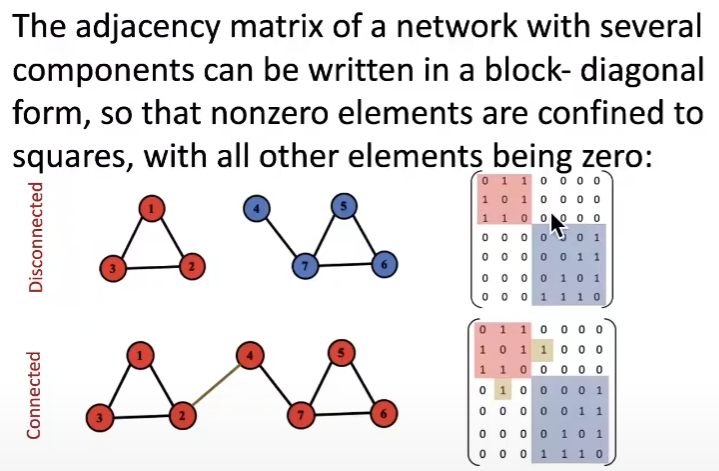
노드는 총 7개가 있고, 4번과 2번이 절단되었기 때문에, 4x2(2x4)에서는 0으로 표현되었습니다.
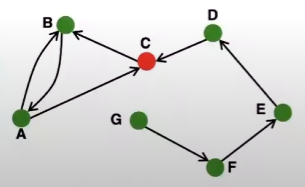
방향성(DAG) 그래프도 연결성을 나타낼 수 있는데요, 아래와 같이, 교류(?)가 활발한 node의 군집을 나타낼 수 있습니다. 이를 SCCs라고 정의하셨네요.

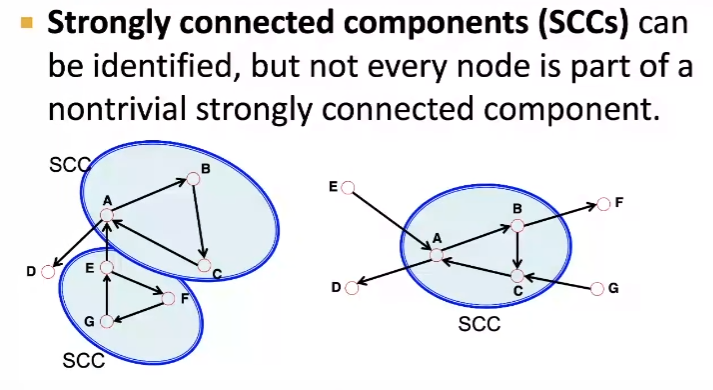
그래프 표현의 변환

한 형식의 그래프 표현에서 다른 형식으로 변환하는 것은 가능하지만, 비용(resource)이 발생할 수 있습니다.
그래프 표현의 예시로는 실제 그래프 데이터셋에서는 다양한 그래프 표현 방법이 사용되며, 이들은 데이터의 크기, 복잡성, 분석 목적에 따라 달라질 수 있습니다.