[Graph] CS224W: Traditional methods for ML on graphs (4)

Immanuel·2023년 10월 13일

CS224W

목록 보기

4/5

Summary Lecture 2.1
1. 노드 / 링크 / 그래프 단위로 머신러닝 예측 모델을 만들 수 있습니다.
2. 이번 강의는 Node Level의 prediction에 대해 설명합니다.
3. 노드의 예측에는 4가지를 고려해아 합니다.

Node Degree: 노드의 차수

Node Centrality: 노드의 중심성이며, Eigenvector centrality와 betweenness centrality가 있습니다.

Clustering coefficient: 노드 군집성을 나타냅니다. 소규모 그래프 커뮤니티 분류에도 활용될 수 있습니다.

Graphlets: 그래프 내, sub그래프를 표현하는데 적절하며, 전반적인 그래프 구조를 이해하는데 도움이 됩니다.

Traditional ML Pipeline

이번 강의에서는 그래프에서 전통적인 머신러닝에 대해 강의합니다. 그래프에서 우리가 머신러닝을 적용할 수 있는 분야는 Node / Link / Graph 수준으로 분류합니다.

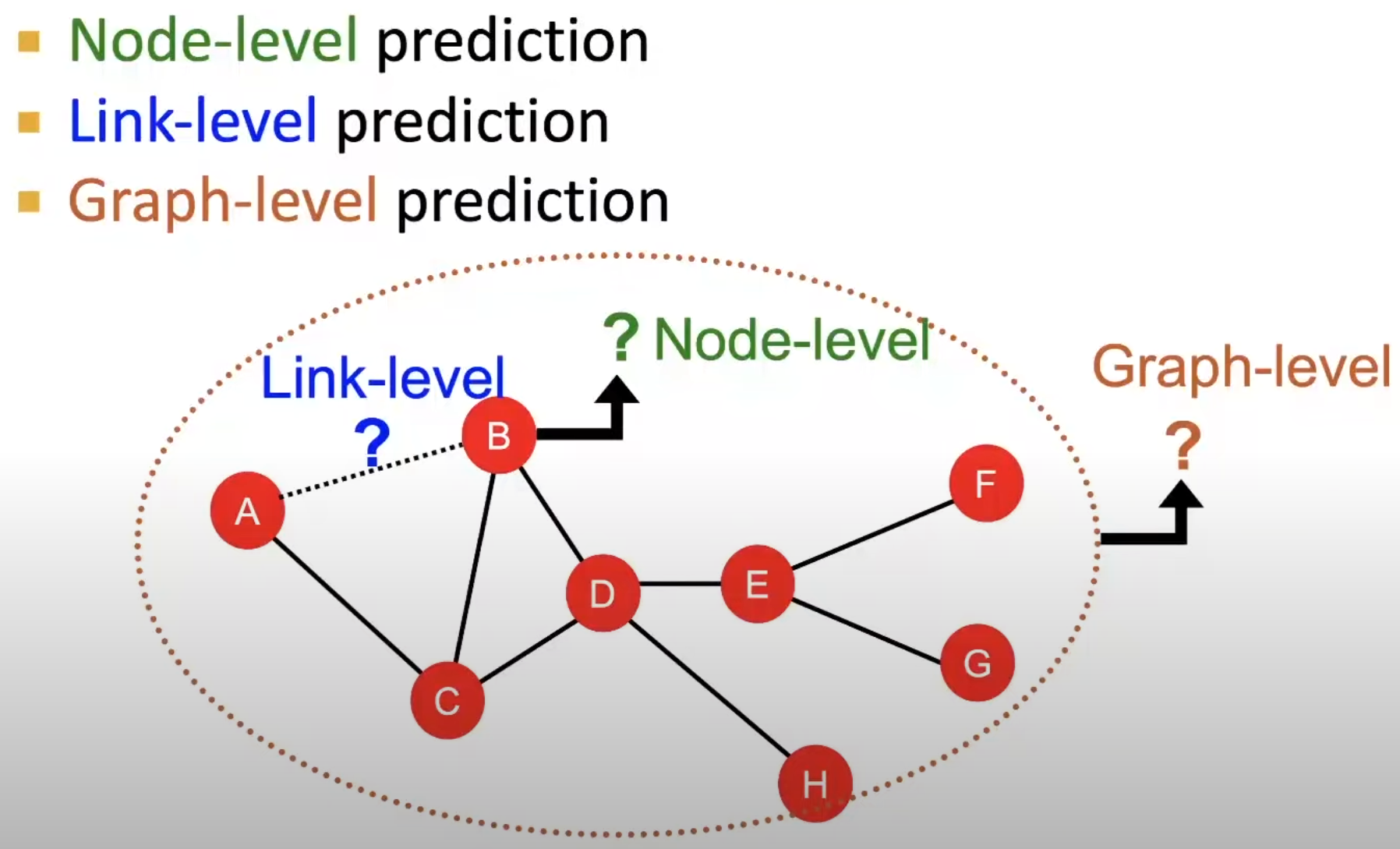
Machine Learning in Graphs

이번 강의에서의 목표는 Object(노드, 엣지 등) 세트에 대해, 예측하는 것입니다.
설계해야 할 부분은 크게 3가지로 아래와 같이 설명합니다.

Features: d차원 벡터
Objects: Nodes, edges, sets of nodes, entire graphs
Objective function: 우리가 예측하려는 Label이 무엇인지?

쉽게 수식으로 이해하자면, $G = (V, E)$ 가 주어졌을 때, $f: V -> R$ 을 학습하는 것입니다. 여기서 관건은 함수 $f$ 를 어떻게 학습시킬지가 되겠습니다.

Node-level Tasks

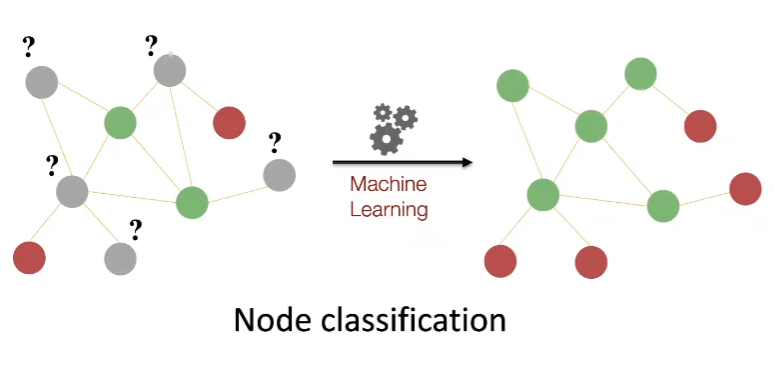
강의에서는 그래프가 주어지고, 머신러닝으로 노드의 색상 분류를 진행하고자 합니다. (Node classification)
단순 직관적으로 보았을 때, 빨간색 노드는 하나의 edge를 가지고 있고, 초록색 노드는 2개 이상의 edges를 가지고 있네요. 즉, 위와 같이 우리는 특정 토폴로지 패턴을 설명하는 기능이 필요하며, 이는 네트워크 맥락에서 노드의 위치를 특성화하는 것입니다.

그리고, 강의에서는 이를 가능하게 만드는 4가지 접근법에 대해 설명합니다.

노드 예측 시, 노드 주변 네트워크 구조를 사용할 수 있습니다.

노드 중심 측정 개념을 통해, 노드의 중요성과 위치에 대해 생각할 수 있습니다. 이는 아마, 이전에 그래프 구조 부분에서 d차원 그래프가 구성할 수 있는 노드 네트워크와 연관된 개념인 것 같습니다.

클러스터링 계수

Graphlets(클러스터링 계수를 확인한 후, Graphlets 이라는 개념으로 일반화합니다)

Node Features: Node Degree

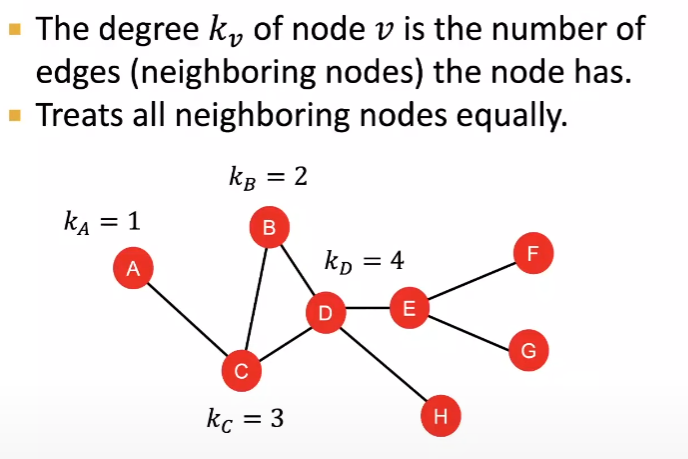
위 이미지에는 그래프와 노드의 차수를 나타내었습니다. 방향성이 없는 그래프네요.
보시다시피, 연결되어있는 degree만으로 분류하기는 어렵습니다. 예를 들면, 노드C와 노드E는 동일한 차수 값이므로, F, G, A, B, D를 구분하기 어렵습니다.

Node Features: Node Centrality

위와 같이, 노드의 차수만을 활용하는 것은 문제점이 있습니다. 여기서 노드 중심성 측정을 통해, 노드가 얼마나 중요한지에 대해 초점을 맞춥니다. 이러한 개념으로 모델링할 수 있는 방법은 다음과 같습니다.

고유벡터의 중심성을 측정합니다.

주어진 노드가 중심과 얼마나 가까운지 파악합니다.

Eigenvector centrality

우선, 고유벡터 중심성이 무엇인지 정의하겠습니다.
중심성을 정의하는 방법 중, Eigenvector centrality(아이겐벡터 중심성) 방법이 있습니다.

아이겐벡터 중심성은 그래프 내, 노드의 영향력을 측정하는 방법 중 하나입니다.
노드가 그래프 내에서 얼만큼 중요한 역할을 하는지 나타냅니다.
특정 노드가 높은 점수를 가진 다른 노드들에게 연결되어 있을 때, 그 노드의 점수가 높아지는 방식으로 작동합니다.
즉, 많은 수의 높은 점수를 가진 노드들이 특정 노드와 연결되어있을 때, 그 노드는 높은 아이겐벡터 중심성을 가집니다.

찾아보니, 아이겐벡터의 개념은 1895년 체스 토너먼트의 점수를 매기는데 처음 사용되었다고 하네요. 이후 Google의 PageRank 알고리즘과 Katz 중심성 등에서 변형되어 사용되었습니다.
노드 $vi$ 의 아이겐벡터 중심성 $EC(vi)$ 는 아래와 같이 정의됩니다.

$E C (v_{i}) = \frac{1}{λ} \sum_{j \in N (v_{i})} a_{i j} E C (v_{j}) <annotation encoding="application/x-tex"$

각 수식의 의미를 정의하자면,

$aij$ 는 인접 행렬 A의 항목입니다.
$N(v_i)$ 는 노드 $v_i$ 의 이웃 노드 집합입니다.
$max(lambda)$ 는 가장 큰 고유값, $lambda$ 는 노드의 고유값 입니다.

이 수식은 각 노드의 중심성 점수가, 그 노드의 이웃들의 중심성 점수의 합에 비례함을 나타냅니다. 이는 일반적으로 가장 큰 고유값에 대응하는 고유벡터로 계산됩니다. 그리고 이 고유벡터의 각 성분은 그래프 내, 해당 노드의 상대적인 중심성 점수를 제공합니다.

Betweenness cetrality

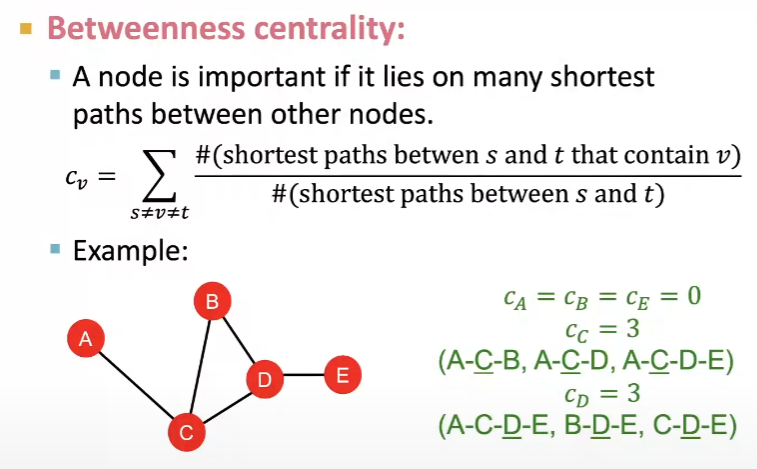
Betweenness centrality로, 중심성을 계산하는 다른 방법이 있습니다.

컨셉은 그래프 내의 모든 노드간 최단 경로 중, 해당 노드를 통과하는 경로의 수를 측정합니다.
즉, 더 많은 최단 경로가 특정 노드를 통과할수록, 그 노드의 betweenness centrality는 높아집니다.

수식은 아래와 같이 정의됩니다.
$C_{B} (v) = \sum_{s, t \in V} \frac{σ (s, t ∣ v)}{σ (s, t)} <annotation encoding="application/x-tex"$

각 수식의 의미를 정의하자면,

$v$ 는 그래프의 노드 집합입니다.
$Sigma(s, t)$ 는 노드 $s$ 와 $t$ 사이의 최단 경로 수입니다.
$Sigma(s, t|v)$ 는 노드 $s$ 와 $t$ 사이의 최단 경로 중, 노드 $v$ 를 통과하는 경로 수입니다.

이는 그래프 내에서 정보의 흐름에 대한 노드의 영향력을 감지하는 방법으로 사용되며, 그래프의 한 부분에서 다른 부분으로 연결되는 다리 역할을 하는 노드를 찾는데 사용됩니다.

Node Features: Clustering Coefficient

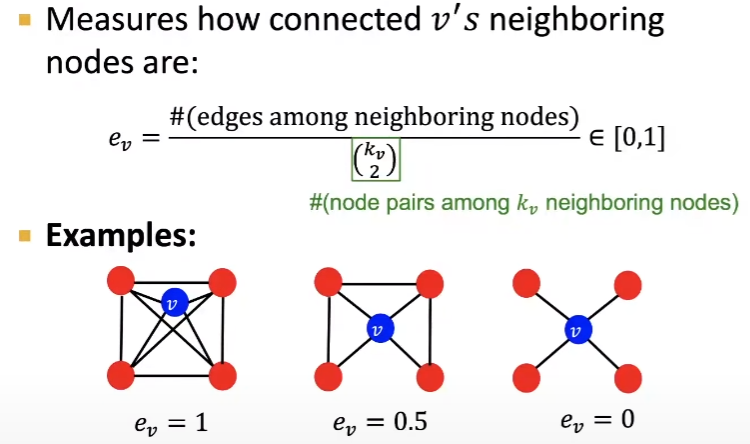
Clustering Coefficient는 노드가 그래프 내에서 얼마나 중요한 역할을 하는지를 나타냅니다. Clustering Coefficient는 그래프 내의 노드들이 얼마나 군집화되어 있는지를 측정합니다.
우선, Clustering Coefficient는 다음과 같이 정의됩니다.

노드 $n$ 의 지역 군집 계수 $C_n$ 은 $n$ 의 이웃들이 서로 얼마나 연결되어 있는지를 설명합니다.
$C_n$ 을 계산하기 위해, 노드가 참여하는 삼각형의 수 $T_n$ 과 노드의 차수 $d_n$ 을 사용합니다.
즉, Clustering Coefficient는 노드의 이웃 사이에 가능한 최대 연결 수 대비, 실제 연결 수의 비율을 나타냅니다.
이 값은 0과 1사이에 있으며, 1은 노드의 모든 이웃이 서로 연결되어 있음을, 0은 노드의 어떤 이웃도 연결되어 있지 않음을 나타냅니다.

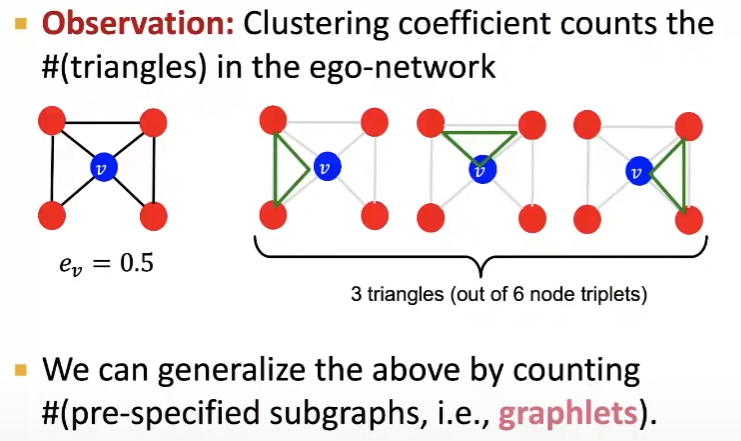
따라서, Clustering Coefficient는 그래프 내에서 정보의 흐름에 대한 노드의 영향력을 감지하는 방법으로 사용되며, 그래프의 한 부분에서 다른 부분으로 연결되는 다리 역할을 하는 노드를 찾는데 사용된다고 합니다.

Node Features: Graphlets

Graphlets는 그래프 이론에서 서브 그래프를 나타내며, 이는 그래프 내에서 연결된 패턴을 나타냅니다. Graphlets의 빈도는 네트워크 구조를 평가하는데 사용될 수 있습니다.

이는 그래프의 특정 부분을 나타내며, 전반적인 구조를 이해하는데 도움이 된다고 합니다.
예를 들어, 3개의 노드로 구성된 Graphlets은, 그래프 내에서 3개의 노드가 어떻게 연결되어 있는지를 나타냅니다.

Graphlets는 네트워크 분석에서 중요한 역할을 하는데, 이것은 네트워크 내에서 복잡한 패턴과 관계를 식별하고 이해하는데 사용될 수 있다고 합니다. 또한, 네트워크 분류 성능을 향상시키는데 중요한 역할을 한다고 합니다.

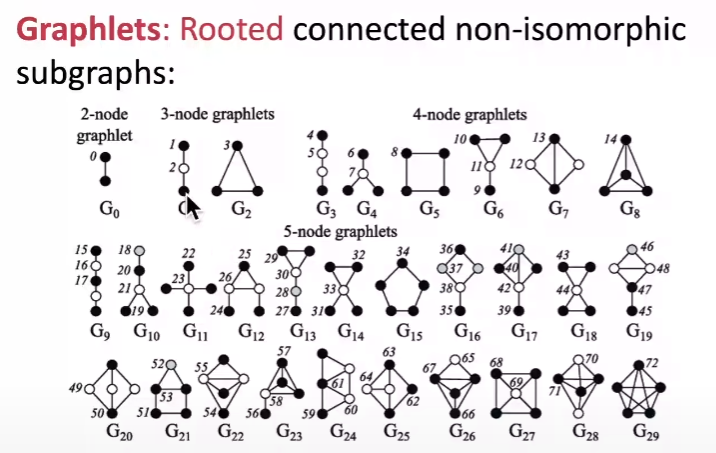
추가로, 해당 강의에서 Graphlet Degree Vector(GDV)라는 개념을 알려주셨는데요, 해당 개념에 대해 잘 이해하지 못하여 구글링으로 정리하였습니다.
GDV는 Graphlets를 사용하여, 각 노드의 이웃 관계를 표현하며, 어떤 Graphlets에 연결되어 있는지, 연결의 수는 얼마나 되는지를 나타내는 vector라고 합니다. 이 벡터는 노드의 local network 구조를 측정하는데 사용되며, 두 노드의 GDV를 비교함으로써 구조적 유사성을 측정할 수 있다고 합니다.

그러나, Graphlets의 수는 노드 수가 증가함에 따라, 빠르게 증가할 수 있으므로(위 이미지와 같이), 일반적으로 2-5개 노드로 구성된 Graphlets만을 사용하여, 노드의 GDV를 표현한다고 합니다.

Link-level prediction Task: Recap

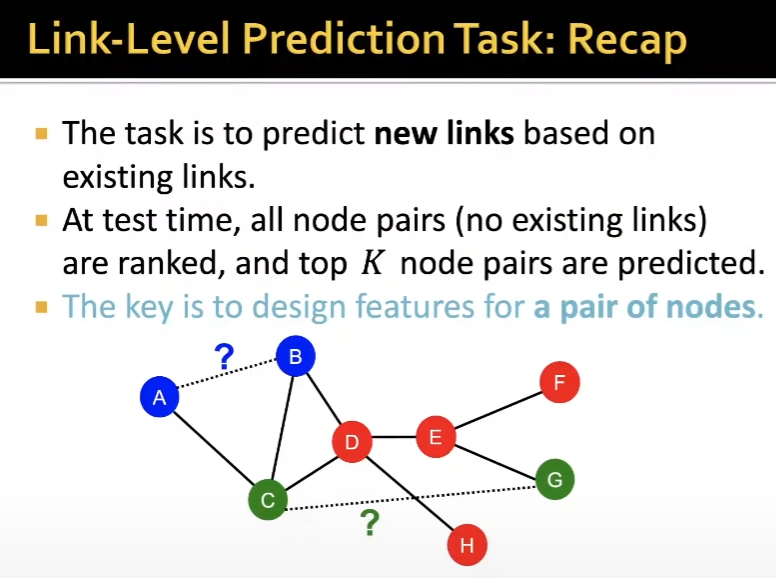
Link(edge) 예측은 소셜 네트워크에서 친구 추천 등의 방법으로 활용될 수 있습니다. 이를 수행하기 위해서는 두 노드 사이의 관계를 특성화하는 방법이 필요하다고 합니다. 이를 위해서, 아래 3가지 접근법을 소개합니다.

Node-based features: 두 노드의 특성을 사용하여, 엣지의 존재 가능성을 측정합니다. 예를 들어, 두 노드의 차수, 중심성, 군집 계수 등을 사용할 수 있습니다.

Topology-based features: 그래프의 전체적인 구조를 사용하여, 엣지의 존재 가능성을 측정합니다. 예를 들어, 두 노드 사이의 최단 경로 길이, 공통 이웃 수, Jaccard계수 등을 사용할 수 있습니다.

Graphlet-based features: 그래프의 지역적인 패턴을 사용하여, 엣지의 존재 가능성을 측정합니다. 예를 들어, 두 노드가 참여하는 Graphlets의 수나 종류를 사용할 수 있습니다.

전통적인 머신러닝 파이프라인은 다음과 같습니다.

feature extraction: 각 엣지에 대해, 위에서 소개한 접근법들을 사용하여, 특성 벡터를 생성합니다. 이 때, 엣지가 실제로 존재하는 경우와 존재하지 않는 경우를 모두 고려해야 합니다.

Model training: 특성 벡터와 엣지의 존재 여부를 입력으로 하여, 분류 모델을 학습합니다. 예를 들어, 로지스틱 회귀나 SVM등을 사용할 수 있습니다.

Model evaluation: 학습된 모델을 테스트 데이터에 적용하여, 성능을 평가합니다. 예를 들어, 정확도나 ROC 곡선 등을 사용할 수 있습니다.