완전탐색 vs 투 포인터
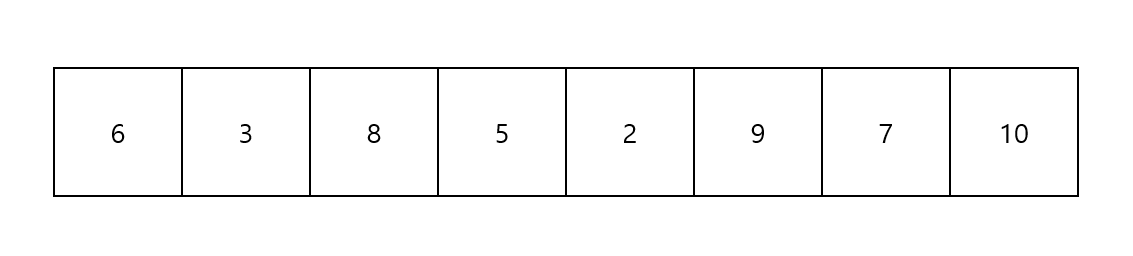
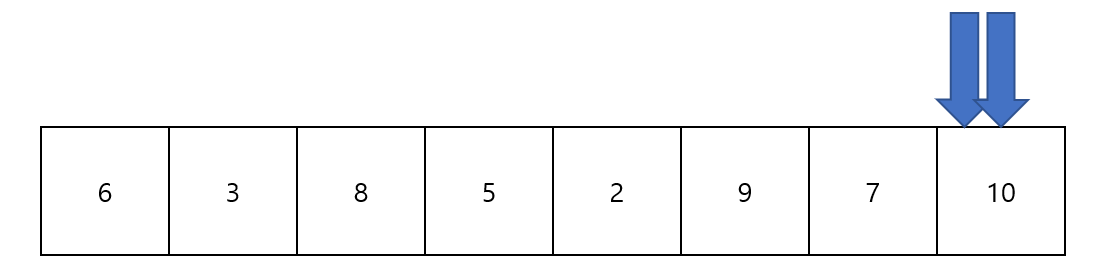
다음과 같은 값들이 들어가 있는 배열에서 합이 25 이하인 최대 길이를 구한다고 가정했을때, 이를 처음부터 끝까지 완벽하게 탐색하면 시간복잡도는 O(N²)가 나올 것이다.
6이랑 3이랑 비교해보고, 또 8이랑 해보고,, 배열의 크기가 커진다면 계산하던 컴퓨터는 중간에 뻗어버릴 것이다..!
이런 시간 복잡도를 현저하게 줄일 수 있는 방법이 투 포인터이다. 말 그대로(two pointer) 두개의 포인터를 가지고 탐색을 하는 알고리즘이다.
투 포인터 맛보기
맛보기용으로 위의 문제를 투포인터를 이용해 풀어보도록 하겠다.
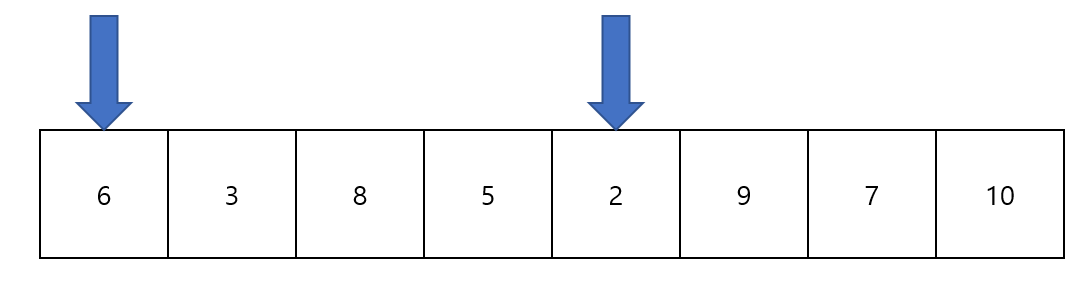
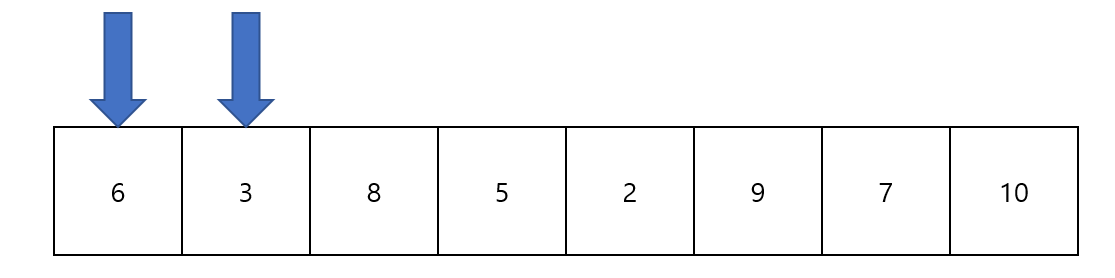
처음에는 두 포인터 모두 초기값을 0으로 잡는다. 이때 부분배열의 합은 6이고, 길이는 1이다.
배열의 합이 25를 넘지 않았기 때문에 두번째 포인터의 값을 올려준다.
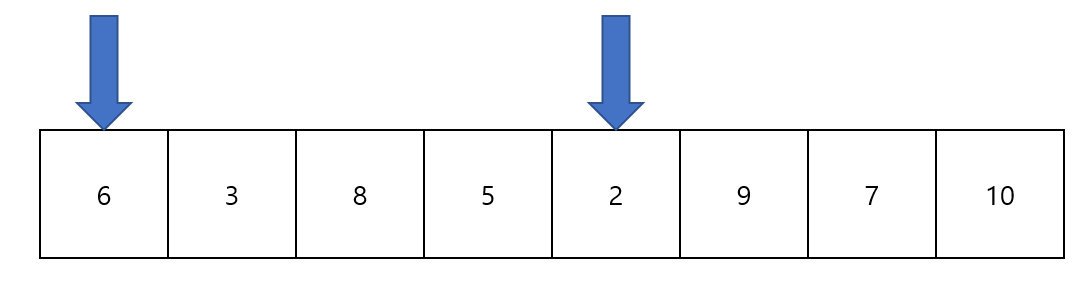
두번째 포인터의 값이 올라가서 현재 부분배열의 합은 9이고, 길이는 2가 되었다. 이 작업을 합의 최대값이 25가 되기 직전까지 반복한다.
각 포인터가 6과 2를 가리키는 순간, 부분배열의 합은 24가 되었고, 배열의 길이는 5가 되었다.
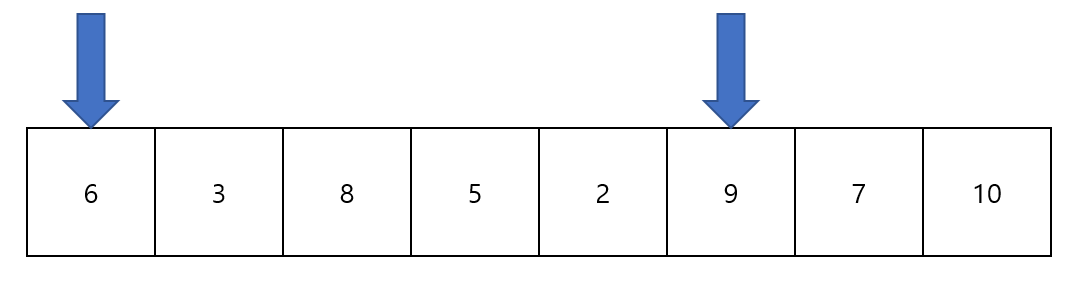
아직 25를 넘지 않았기 때문에 두번째 포인터를 올려준다.
이 순간 부분배열의 합이 33이 되면서 원래 조건인 "25 이하"에 위배되었음으로 현재까지의 최대 길이는 포인터가 6과 2를 가리키고 있던 부분배열의 길이인 5가 되는 것이다.
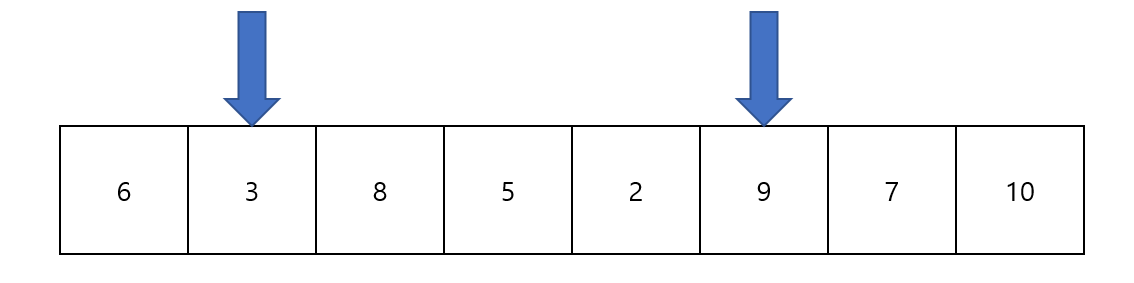
이때는 아직 사용하지 않은 첫번째 포인터를 올려준다.
첫 번째 포인터를 올렸음에도 불구하고 부분배열의 합이 25를 넘어가기 때문에, 합이 25를 넘어가지 않을때까지 첫번째 포인터를 올려준다. 이 과정에서 두 포인터들이 움직이는 조건을 알 수 있다..!
첫 번째 포인터가 올라가는 조건은 부분배열의 합이 25 초과일때
두 번째 포인터가 올라가는 조건은 부분배열의 합이 25를 넘기지 않았을 때
첫 번째 포인터가 움직이는 조건으로 저게 가능한 이유는, 첫번째 포인터를 올리는 순간 올리기 전 인덱스에 들어있는 값만큼 부분배열의 합에서 빼주는 것과 같기 때문이다.
결과적으로 첫 번째 포인터가 배열 끝까지 가면 더 이상 탐색이 불가능하므로 탐색을 종료한다.
이 과정을 코드로 나타내면 다음과 같다.
맛보기 문제 코드
#include <stdio.h>
int main(){
int arr[8] = {6, 3, 8, 5, 2, 9, 7, 10};
int start = 0, end = 0, maxLen = 0;
while(start < 8){
int sum = 0;
for (int i = start; i <= end; i++){
sum += arr[i];
}
if (sum > 25) start++;
else {
if (maxLen < end - start + 1) maxLen = end - start + 1;
end++;
}
}
printf("%d", maxLen);
return 0;
}불필요한 계산을 더 줄일수는 있지만 투포인터를 처음 접하는 독자를 위해 쉽게 이해하도록 작성해보았다.
처음에는 두 포인터 모두 0으로 초기값을 맞춰놓고, 반복문을 돌면서 각 부분배열의 총 합을 구한 후 비교값보다 큰지 작은지를 if문으로 분기처리를 시켜준다.
만약 25보다 크다면 첫 번째 포인터를 올려서 부분배열의 합을 줄여주고,
그렇지 않다면(= 작거나 같다면) 그 부분이 부분배열의 최대 길이인지 판별 후 맞다면 최대 길이를 갱신, 아니라면 그냥 두고 두 번째 포인터를 올려준다.
탐색이 끝나면 최대 길이를 출력하고 마무리한다.
이 때 시간 복잡도는 배열의 크기만큼 반복문이 돌기 때문에 O(n) 정도 걸린다. 부분배열의 합을 구하는 for문은 시간 복잡도에 큰 영향을 주지 않기 때문에 제외한다.
이런식으로 혼자서 답을 찾을때까지 1ㄷ1로 완전탐색하는것보다, 이렇게 투포인터를 활용해 둘이서 2ㄷ1로 답을 찾아나가면 훨씬 빠르게 원하는 결과를 도출해낼 수 있다.
투 포인터의 종류
투 포인터를 사용하는 방식은 두가지가 있다. 앞서 봤던 두 포인터 모두 0번째 인덱스부터 시작하는 방법과 배열의 양쪽 끝에서 포인터를 시작하는 방법이 있다.
투포인터는 상황에 따라 유연하게 사용할 줄 아는 능력을 기르는게 중요한데, 문제를 많이 풀어보면 어느 순간에 어떤 투포인터를 사용해야 하는지 확실하게 느껴진다.
약간 힌트를 주자면,,
구간 합이라던가 원소를 여러개 사용해야 하는 구도에서는 0번째 인덱스부터 시작하는 방법,
두 수의 합같이 두 포인터가 가리키는 부분만 사용하는 구도에서는 양쪽 끝에서 시작하는 방법
이게 정답이라고 말할수는 없지만, 필자가 이해한 유연한 투포인터 사용법은 이렇다. 이 글을 읽는 독자분들도 문제를 풀어보며 투포인터가 무엇인지, 어떻게 사용해야 하는지 직접 느껴보기를 바란다.
투 포인터와 정렬..?
투 포인터에게 있어서 정렬은 거의 필수적이다. 정렬이 필요한 투 포인터 문제를 풀어보며 이해해보자.
먼저 풀어보고 싶은 사람은 --->두 수의 합
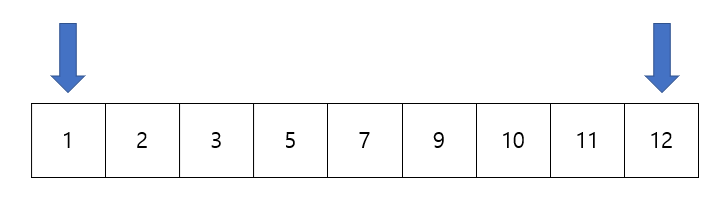
두 수의 합이 13이 되는 조합의 갯수를 구하는 문제이다. 두 포인터가 가리키는 부분만 사용하니까 양쪽 끝에서 시작하는 투포인터 기법을 사용할 수 있다.
시작 인덱스가 0과 n-1이라면 첫번째 합은 5 + 11 = 16이다. 13보다 크기 때문에 포인터를 옮겨주어야 한다. 그런데 어떤 포인터를 옮겨야 할까? 포인터를 옮겨도 무슨 숫자가 나올지 모르는데 그러면 완전탐색해야 하는거 아닌가?
라고 생각할 수 있다. 하지만 여기서 정렬을 사용한다면?
예제에서 입력된 배열이 이렇게 바뀌게 되고, 정렬 덕분에 두 포인터가 조건에 따라 이동할 수 있는 근거가 생기게 된다.
두 포인터의 합이 13보다 크다면 오른쪽 포인터를 내려서 포인터의 합을 작게 만들어주고,
두 포인터의 합이 13보다 작다면 왼쪽 포인터를 올려서 포인터의 합을 크게 만들어준다.
이 과정이 가능한 이유는 오른쪽 포인터 왼쪽에 있는 값들은 무조건 오른쪽 포인터가 가리키는 값보다 무조건 작을수밖에 없다. (정렬을 시켰기 때문..!)
왼쪽 포인터도 마찬가지이다. 오른쪽에 있는 값들은 무조건 왼쪽 포인터가 가리키는 값보다 클 것이므로 13보다 작다면 올려서 합을 키워 줄 수 있는 것이다.
이를 코드로 옮기면 다음과 같다.
#include <stdio.h>
#include <stdlib.h>
int comp(const void *a, const void *b) {
return *(int *) a - *(int *) b;
}
int main() {
int n, x, arr[100000], count = 0;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &arr[i]);
}
scanf("%d", &x);
qsort(arr, n, 4, comp);
int j = 0, k = n - 1;
while (j < k) {
int sum = arr[j] + arr[k];
if (sum < x) j++;
else if (sum > x) k--;
else {
count++;
j++, k--;
}
}
printf("%d", count);
}정렬은 알잘딱하게 해주고 포인터는 각각 양쪽에서 시작하도록 만든 후 반복문을 돌려준다.
이때 반복문의 조건이 j < k인 이유는 결국 두 포인터 모두 중간 지점에서 만날 것이고, 시작 포인터가 끝 포인터랑 겹치는 순간은 탐색이 끝났음을 의미한다.
만약 합이 x보다 크다면 j++을 해서 합을 올려주고, 작다면 k--를 해서 값을 낮춰준다.
만약 합과 x가 같다면 조합을 찾았기 때문에 count 변수값을 올려주고 각 포인터를 이동시켜준다.
이 문제에서는 n개의 서로 다른 양의 정수라고 했기 때문에 같은 조합이 생길 수가 없어서 두 포인터를 모두 이동시켰다.

이렇듯 투포인터에 정렬이 필요한 이유도 알아보았다.
슬라이딩 윈도우
두 포인터 이야기가 나오면 얘도 세트로 묶이곤 한다. (좀 비슷하긴 하다)
알고리즘 자체가 창문을 미는 행위, 한국식으로 미닫이문과 비슷하게 생겼다.
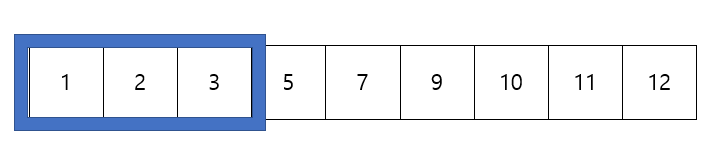
이런식으로 배열 크기를 3이라고 가정했을때 가장 큰 부분배열의 합을 구하는 문제에서 자주 사용된다.
슬라이딩 윈도우는 한 칸 앞으로 갈때마다 다음 값이 더해지고 이동하기 전 첫번째 값이 빠지기 때문에 굳이 3개를 더해주는 반복문을 쓸 필요가 없어서 더 효율적으로 문제를 해결 할 수 있다.
슬라이딩 윈도우도 코드로 나타내면 다음과 같다.
#include <stdio.h>
int main() {
int arr[10] = {1, 2, 3, 4, 5, 7, 9, 10, 11, 12};
int rs = arr[0] + arr[1] + arr[2], sum = rs;
for (int i = 3; i < 10 - 3; i++){
sum = sum + arr[i] - arr[i - 3];
if (rs < sum) rs = sum;
}
printf("%d", rs);
}초기에는 3칸 배열의 합을 구해놓고, i값이 증가할 때마다 새로운 값을 더해주고 오래된 값은 빼주면서 가장 큰 합을 갱신하는 코드이다.
마무리
슬라이딩 윈도우는 배열의 크기가 항상 고정적이지만, 투 포인터는 그렇지 않다는 것이 둘의 차이점이다. 상황에 따라 적절하게, 유연하게 사용할 줄 아는 능력을 기르는 것이 정말 중요하므로 꼭 읽고 넘어가지 말고 한 문제만이라도 풀어봤으면 좋겠다.
3개의 댓글
Each time it happens, I feel like something has crashed, broken, or reset, and I have to track down where I left off. https://doramasflix.to/



Full search and two pointer are two different algorithms used for solving problems in computer science.
Full search, also known as brute force, involves checking all possible combinations of elements to find a solution. It is a straightforward approach, but it can be time-consuming and inefficient for large datasets. Full search is usually used when the problem size is small and the number of possible combinations is manageable.
Two pointer, on the other hand, is a technique used for solving problems that involve finding pairs or combinations in a sorted array. The algorithm uses two pointers, one starting from the beginning and the other from the end, to traverse the array and find the solution. The two pointers move towards each other until they meet or a solution is found. Two pointer is a more efficient algorithm compared to full search, especially for large datasets.
In summary, full search and two pointer are two different algorithms used to solve different types of problems in computer science. The choice of algorithm depends on the problem and the size of the dataset. ACE Flare MetaBank