에라토스테네스의 체

유찬홍·2022년 12월 24일

에라토스테네스의 체 알아보기

마치 체로 치듯이 수를 걸러낸다고 하여 '에라토스테네스의 체'라고 부른다.

나무위키에서는 에라토스테네스의 체를 이렇게 설명하고 있다. 아직 잘 모르겠다면 아래 움짤을 보도록 하자.

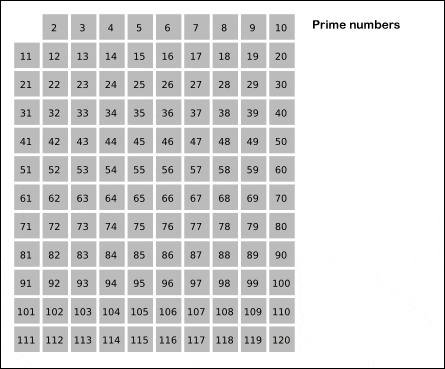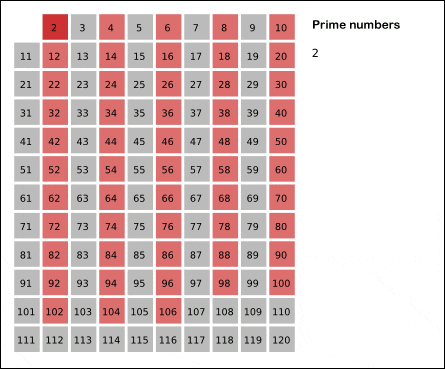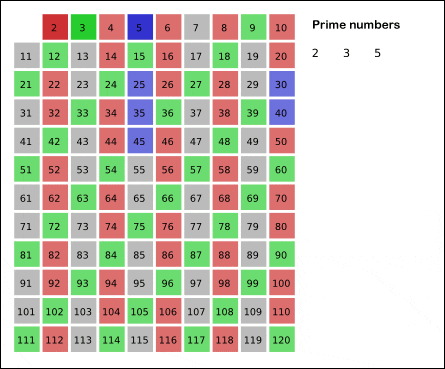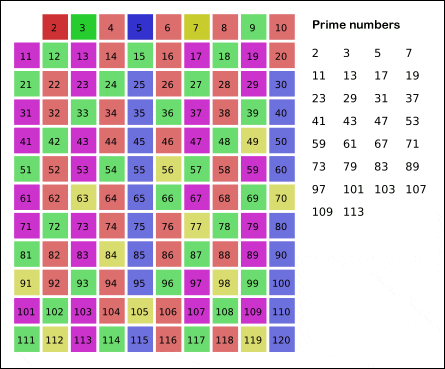
2를 제외한 2의 배수, 3을 제외한 3의 배수...색칠되지 않은곳의 배수들을 제거하다보면 어느새 소수들이 다 찾아져 있다.
이렇게 체에 거르듯이 숫자를 거르다 보면 체에는 소수가 남게 되고 이 방식을 "에라토스테네스의 체"라고 부른다.

코드로 보는 에라토스테네스의 체

핵심 코드는 다음과 같다.

int arr[MAX_SIZE + 1] = {0};
    int len = sqrt(MAX_SIZE);
    for (int i = 2; i <= len; i++) {
        if (arr[i] == 0) {
            for (int j = i * i; j <= MAX_SIZE; j += i) {
                arr[j] = 1;
            }
        }
    }

1. 구하고 싶은 크기 + 1 만큼 배열을 만들고, 0으로 초기화 해준다.

배열의 인덱스를 사용해서 구할거기 때문에 1을 더해준다. (대신 arr[0]은 안써요!!)

2. 구하고 싶은 크기의 제곱근만큼 첫 for문을 돌려준다.

에라토스테네스의 체를 공부하면서 이 부분이 제일 헷갈렸다. 왜 제곱근까지만 for문을 돌리는걸까?
100까지의 소수를 찾는다고 가정해보자. 2의 배수..3의 배수...10의 배수까지 다 찾아서 제거했다. 11의 배수를 제거한다면 뭘 제거해야 할까? 22는 2의 배수, 33은 3의 배수...99는 9의 배수, 110은 10의 배수, 정작 제거하지 않은 부분은 자기 자신인 11부터인데 사실 여기까지 오면 100을 뛰어넘어버려서 지우는 의미가 없어진다. 그렇게 만들어지는 식이 i^2 <= MAX_SIZE이다. 이렇게 for문을 돌리면 MAX_SIZE까지 불필요한 계산이 사라지므로 더 효율적이게 된다.

3. for문을 돌려가며 i의 배수를 제거한다.

두번째 for문에 조건식이 달려있는걸 볼 수 있다. arr 배열의 i번째 인덱스에 0이 있을때만 두번째 for문을 돌린다는 뜻이다. 여기서 아까 처음에 배열을 0으로 초기화한 이유를 엿볼 수 있는데, 우리가 2의 배수를 찾아서 없앤다고 가정했을 때 2를 제외한 4부터 쭉 두번째 for문을 돌면서 각 배열에 1이 저장된다. 그 다음엔 3, 그 다음엔 4의 배수를 없애야 하는데 4는 이미 2의 배수이므로 arr[4]에는 이미 1이 들어가있을 것이고, 덕분에 4의 배수를 제거하려고 해도 2의 배수단에서 이미 제거되어있어서 굳이 아래 for문을 돌릴 필요가 없어진다. if(arr[i] == 0) 덕분에 더 효율적인 코드가 된다..!!

4. 출력한다.

for (int i = 2; i <= MAX_SIZE; i++) {
	if (arr[i] == 0) printf("%d\n", i);
}

마지막으로 2부터 시작해서 arr[i]에 0이 들어가있다면, 소수 판별 단계에서 제거되지 않은 수들이라면 인덱스를 출력해서 소수들을 찾아낼 수 있다.
소수들의 갯수를 구하는 문제를 푼다면 count++하면서 찾으면 되는거고 합을 구하는 문제면 sum += i 하면서 찾으면 되는거고.. 이 부분은 문제에 따라 다르게 변형해가며 사용할 수 있다.