로또 1등을 할 수 있는 경우의 수

일상생활 속 경우의 수

일상생활에서 경우의 수는 많이 숨어 있다. 최단시간으로 안내해주는 네비게이션, 가위바위보 이기기, 시험 문제를 찍어서 90점 이상을 넘길 확률 등등 우리는 매 순간순간마다 선택을 마주하고, 최대한 좋은 결과를 얻어내기 위한 경우의 수를 구하곤 한다.

순열과 조합

경우의 수를 구하기 위해선 고등학교때 배운 순열과 조합을 주로 사용한다.
다만 상황에 따라서 올바른 방법을 택해야 하는데, 조합은 순서가 중요하지 않을 때, 순열은 순서가 중요할 때 사용한다.
예를 들자면,, 대통령 선거에서 대통령과 부통령을 동시에 뽑는다고 가정했을 때, 여기서는 순서가 중요하기 때문에 순열을, 부통령만 두명 뽑는다고 가정했을때는 순서가 중요하지 않기 때문에 조합을 사용한다.
써브웨이에서 나올 수 있는 모든 경우의 수에 순열을 쓰지 않는 이유는 어차피 입에 들어가면 똑같기 때문에(= 순서가 중요하지 않기 때문에) 맛보다는 들어가는 재료들을 더 중요시 해서 조합을 쓴다고 생각하면 편하다.
ex) 한일전 == 일한전

로또 1등이 당첨 될 경우의 수

보너스 번호는 2~3등 가려낼려고 만든거라 제외하고 계산하겠다.
로또는 마구잡이로 섞이는 공을 뽑아서 번호를 맞추는 게임이기 때문에 순서가 중요하지 않아서 조합을 사용한다. 조합 공식은 다음과 같다.

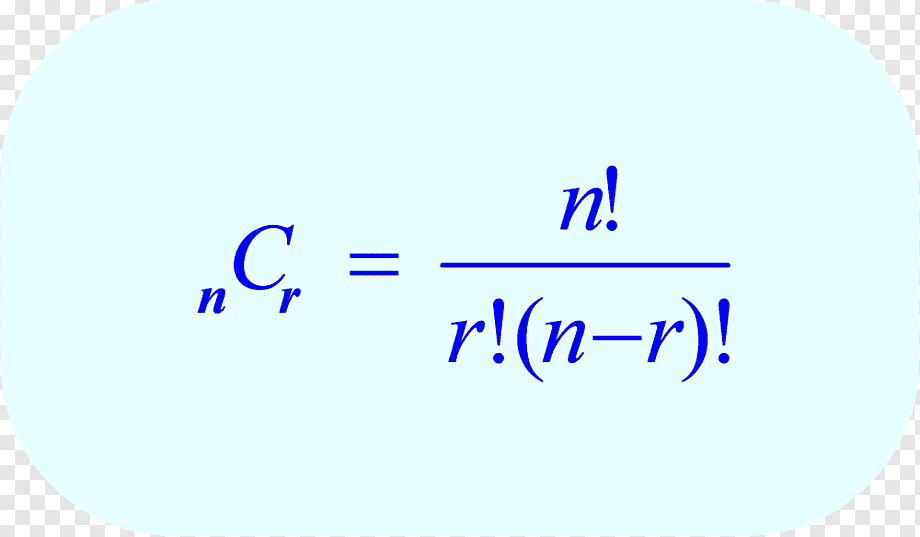
전혀 겁낼거 없다. nCr은 "서로 다른 n개에서 r개를 선택한다~" 라는 뜻이고, 우리는 45개의 번호중 6개를 선택할 것이기 때문에 45C6으로 나타낼 수 있다. 그리고 옆에 있는 공식은 조합을 구하기 위한 공식이다. '!'은 팩토리얼을 나타내는 기호이고, n!은 n부터 1까지 모든 숫자를 곱한 값이라고 생각하면 된다. 그럼 공식에 맞게 대입해서 경우의 수를 구해보자.

n! = 45 x 44 x 43.....3 x 2 x 1 일 것이고
r! x (n-r)! = 6 x 5...3 x 2 x 1 x 39 x 38 ..... 3 x 2 x 1일 것이다.

겹치는 부분을 없애주고 나눠보면

nCr = 45 x 44 x 43 x 42 x 41 x 40 / 6 x 5 x 4 x 3 x 2 x 1

결과는 8,145,060이 나온다. 물론 2등을 계산한다면 5개를 맞출 확률과 보너스 번호까지 계산해야하지만, 1등이니까 다 맞춰야 해서 이렇게 계산해도 된다.
나름 확률로 따지자면 1/8145060이라서 약 0.00001227%가 나온다.
주변에 로또 번호를 돈주고 사는 사람들이 있다면 이 글을 보여주면서 살 필요가 없다는 것을 알려주도록 하자

알고리즘 문제에서 조합을 사용해보자

조합을 이용하는 백준 1010번을 풀면서 필자가 쓴 조합 코드를 이해해보자.

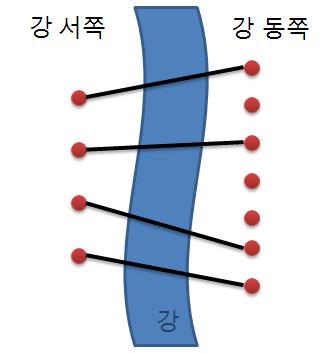
문제를 요약하면 '서쪽에서 동쪽 다리에 연결할때 다리를 겹치지 않게 만들 수 있는 경우의 수 구하기' 라고 할 수 있다.
풀어보고 싶은 사람은 문제 링크를 눌러서 한 번 풀어보길 바란다.
문제 자체는 생긴게 그냥 조합이다. 아까 배운 조합 공식대로 나타내면 4C7이고, 공식에 대입해보면

4C7 = 7 x 6 x 5 x 4 x 3 x 2 x 1 / 4 x 3 x 2 x 1 x 3 x 2 x 1

약분해서 나타내면

4C7 = 7 x 5 = 35

경우의 수는 35가지이다.
이걸 어떻게 코드로 나타낼 수 있을까?
코드로 나타내보기 전에 공식 몇가지만 더 알아보고 가자.

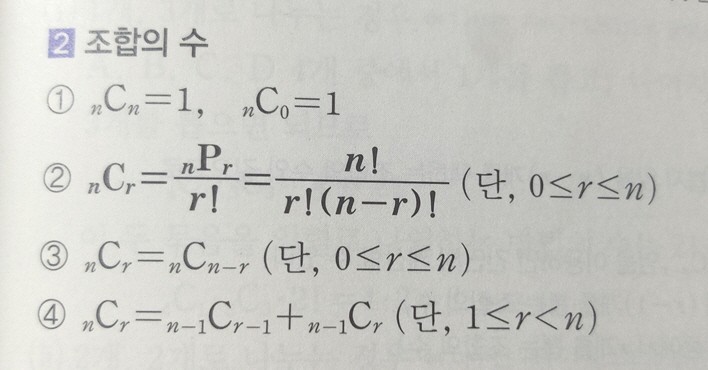
1010번 문제를 풀기 위해서 1번과 4번 공식을 이해해야 한다.(나는 그렇게 풀었다,,)
nCn = 1 이라는 뜻은 n과 r이 같을때, 예를 들자면 3개중 3개를 뽑는 경우의 수는 다 뽑으니까 한 가지만 있을수밖에 없다. nC0 = 1도 0개를 뽑는 경우는 안뽑는 경우 한가지밖에 없으니까 이 수식도 그냥 머릿속에 넣고 다니자.
이 수식을 이해하고 4번 공식이 왜 성립하는지를 이해해보자.
4C2을 예를 들자면,

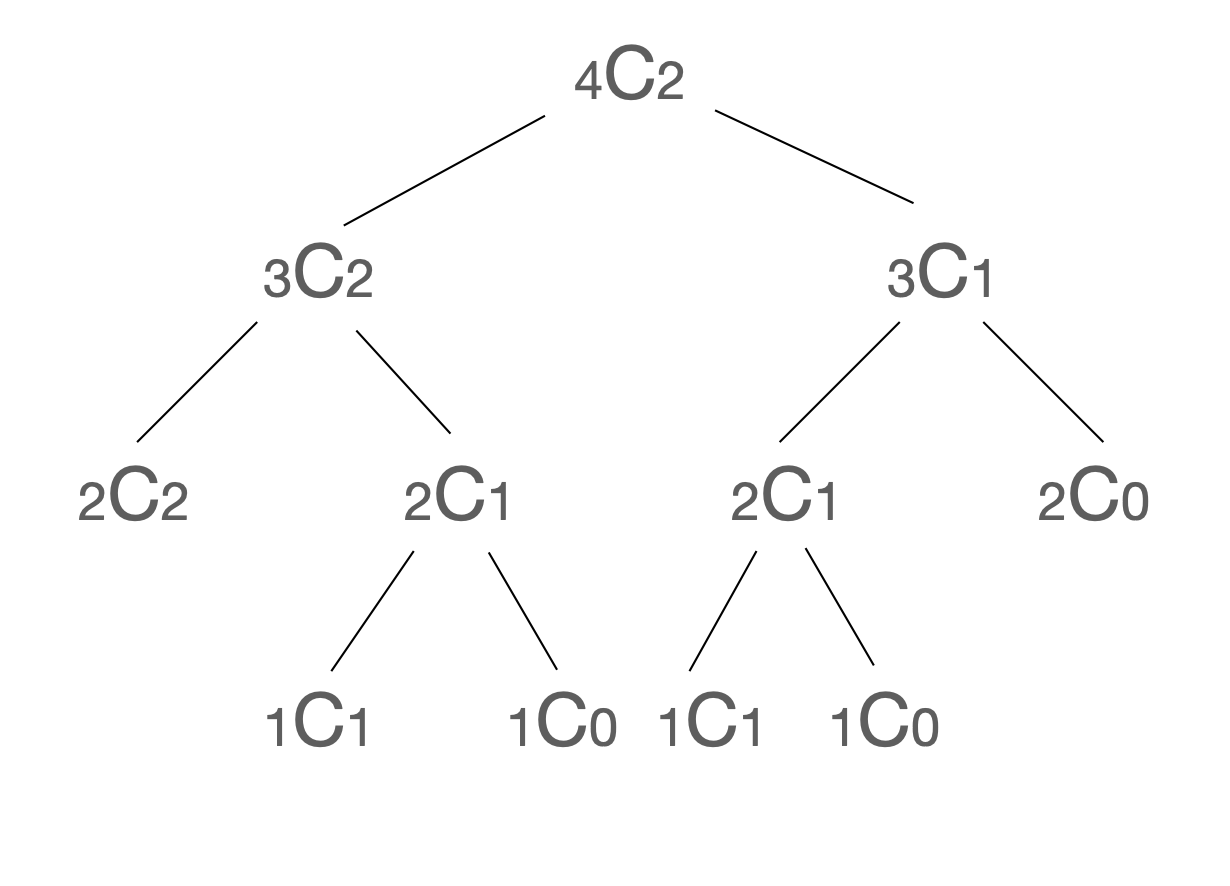
이런식으로 나타낼 수 있고, 1번 수식들에 의해 nCn, nC0인 애들을 1로 바꿔주고 더해가다 보면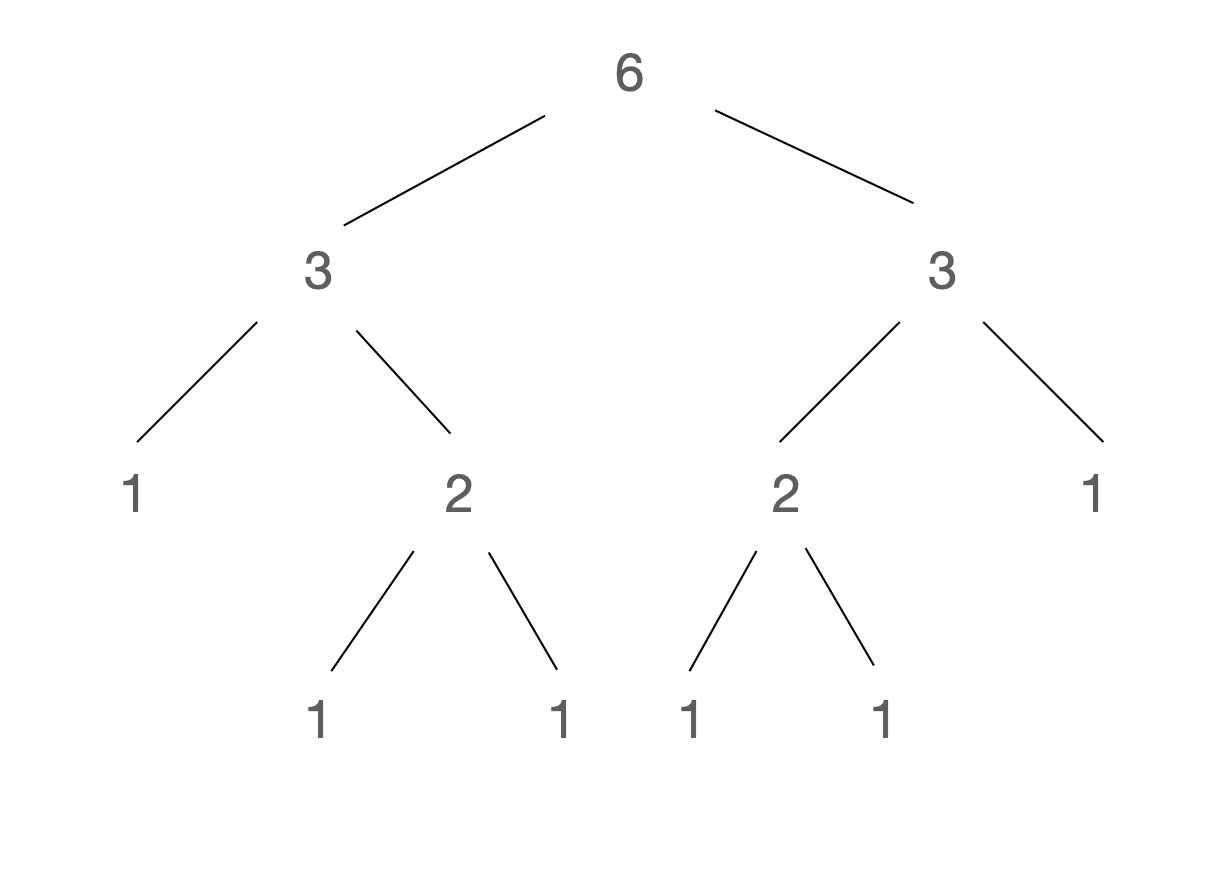
이렇게 된다. 실제로 4C2 = 4 x 3 x 2 x 1 / 2 x 1 x 2 x 1 = 6인것을 알 수 있다.
dp를 알고있는 사람이라면 "이거 뭔가 탑-다운 방식인데??" 라는 생각이 들 것이다.
(dp가 궁금하다면 ㄱㄱ---> 다이나믹 프로그래밍)

코드로 나타내기

문제에서는 nCr에서 n과 r의 값이 최대 30까지 주어지기 때문에 30으로 계속 돌리고 있으면 100% 시간초과가 날 것이다. 메모이제이션 기법을 이용해 결과값을 저장하고, 그렇지 않다면 [n][r]을 구해서 리턴해주는 방식으로 재귀함수를 만들어보도록 하겠다.

int arr[30][30];

int combi(int n, int r) {
    if (n == r) return 1;
    else if (r == 0) return 1;
    else {
        if (arr[n][r] != 0) return arr[n][r];
        arr[n][r] = combi(n - 1, r) + combi(n - 1, r - 1);
        return arr[n][r];
    }
}

아까 알아봤던 1번 수식들을 재귀함수의 종료 조건으로 적어주고, 만약 arr 배열의 [n][r] 칸에 값이 저장되어있다면 그 값을 불러와서 시간복잡도를 줄이고, 아니라면 함수를 호출해서 배열에 값을 저장한 후 마지막에 리턴을 해주면 경우의 수를 구할 수 있다.

전체 코드

c언어가 최고다.

#include <stdio.h>

int arr[30][30];

int combi(int n, int r) {
    if (n == r) return 1;
    else if (r == 0) return 1;
    else {
        if (arr[n][r] != 0) return arr[n][r];
        arr[n][r] = combi(n - 1, r) + combi(n - 1, r - 1);
        return arr[n][r];
    }
}

int main() {
    int input, n, r;
    scanf("%d", &input);
    for (int i = 0; i < n; i++) {
        scanf("%d %d", &r, &n);
        printf("%d\n", combi(n, r));
    }
    return 0;
}

입력받을때 n과 r이 바뀐 이유는 단순히 백준에서 r을 먼저 입력하기 때문이고,, input만큼 돌면서 nCr을 출력해주면 해결 할 수 있는 단순하면서 어려운 문제이다. 물론 다른 방식으로도 문제를 풀 수 있지만, 필자가 작성한 코드는 조합 공식에 기반한 코드라는걸 강조하고 싶다.

시간초과 안나고 해결한 모습이다.