버트런드 러셀 (Bertrand Russel, 1872.05.18 ~ 1970.02.02)
: 큰 기쁨은 쓸데없는 지식을 얻을 때도 느낄 수 있다.
이 포스팅은 '수학리부트' 를 보며 공부한 내용입니다.
많은 응용 분야가 있는 수학의 대표되는 논리 체계인 명제와 집합.
컴퓨터과학이 수학의 응용에서 시작되었음을 생각하면, 우리는 수학의 토대인 논리의 기초를 다질 필요가 있습니다.
명제
참인지 거짓인지 판별할 수 있는 문장이나 수식. (대개 p,q,r 같은 영문자로 표시)
- 참 명제
- 달은 지구의 위성이다
- 2 × 5 = 10
- 거짓 명제
- 다람쥐는 파충류다
- x = 1일때, x² < 1
명제의 진리값 : 명제의 참·거짓. (참: T, 거짓: F)
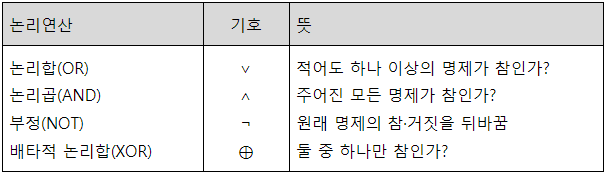
논리연산
숫자에 대한 기본적인 사칙연산을 통해 새로운 숫자가 만들어지는 것처럼, 명제에도 기본적인 연산이 몇 가지 존재합니다. 명제는 진리값을 다루므로 그에 대한 연산은 논리적인 성질을 가지고 있으며, 이러한 논리연산을 명제들에 적용하면 그 결과로 새로운 명제가 만들어집니다.
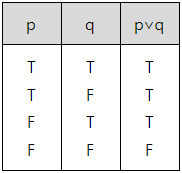
진리표 : 논리연산의 결과를 표 형태로 알아보기 쉽게 나타낸 것.
- 진리표로 나타낸 두 명제 p와 q에 대해 p∨q 연산을 수행한 결과.
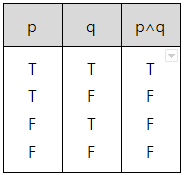
- 진리표로 나타낸 두 명제 p와 q에 대해 p∧q 연산을 수행한 결과.
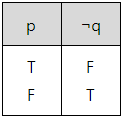
- 진리표로 나타낸 두 명제 p와 q에 대해 ¬q 연산을 수행한 결과.
항진명제 : 항상 참인 명제. ex. p∨¬p
모순명제 : 항상 거짓인 명제. ex. p∧¬p

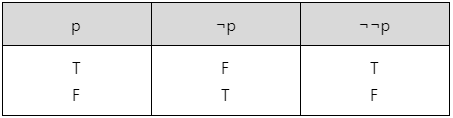
부정(NOT) 연산한 결과를 다시 부정 연산하면 원래 명제의 진리값으로 다시 돌아가게 됩니다.
드 모르간의 법칙(De Morgan's law)
- ¬(p∨q)
위의 식은 OR 연산의 결과를 부정한 것.
OR 연산은 'p나 q 둘 중 하나라도 참이면' 결과가 참이니, OR을 부정했다면 그 반대로 'p와 q 둘 중 어떤 것도 참이 아니면' 연산의 결과가 참이 될 것입니다.
- ¬p∧¬q
동치 : 같은 진리값을 가지는 두 명제. (기호: ≡)
위의 두 식의 진리값은 동일합니다. ➜ ¬(p∨q) ≡ ¬p∧¬q.
마찬가지로, 논리곱 연산을 부정 연산하면 ➜ ¬(p∧q) ≡ ¬p∨¬q.
이러한 두 개의 동치관계는 드 모르간의 법칙(De Morgan's law)이라고 부르며, 복잡한 논리식을 계산할 때 유용합니다.
논리연산의 법칙
숫자의 연산처럼 논리연산에도 몇 가지 기본적인 법칙이 성립합니다.
논리합(∨)은 덧셈과, 논리곱(∧)은 곱셈과 유사한 면이 있고, 진리값 T와 F는 각각 1, 0과 비슷한 성질을 가집니다.
하지만 진리값이 결국 숫자는 아니므로 두 부류의 연산은 엄연히 다르다는 점에 유의해야 함.
숫자의 연산에서 덧셈과 곱셈에 각각 0과 1이라는 항등원이 존재.
- a + 0 = a
- a × 1 = a
논리합에는 F, 논리곱에는 T이라는 항등원이 존재.
- p ∨ F ≡ p
- p ∧ T ≡ p
숫자와는 다르게, 자기 자신에 대한 논리합과 논리곱 연산은 다시 자신으로.
- p ∨ p ≡ p
- p ∧ p ≡ p
논리연산의 법칙
- 교환법칙.
- p ∨ q ≡ q ∨ p
- p ∧ q ≡ q ∧ p
- 결합법칙.
- (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
- (p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
- 분배법칙.
- p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
- p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
분배법칙은 논리연산과 숫자의 연산에 차이가 생깁니다.
숫자의 연산에서는 분배법칙이 a × (b + c) = (a × b) + (a × c)에만 성립하고, a + (b × c) 에는 성립하지 않습니다.
XOR(⊕) 연산
논리연산 중 배타적(exclusive) 논리합, 즉 XOR(⊕) 연산은 두 명제 중 어느 한쪽만 참일 때 결과가 참.
- 교환법칙 : XOR 연산의 성질은 명제의 순서와는 관계가 없으므로 교환법칙이 성립.
- 결합법칙 : 성립. (p ⊕ q) ⊕ r ≡ p ⊕ (q ⊕ r)
'배타적'이라는 성질을 가진 XOR 연산의 특이한 결과.
- T와의 XOR연산 결과 : T ⊕ T ≡ F, F ⊕ T ≡ T
- ➜ 부정 연산자(¬)처럼 동작.
- p ⊕ T ≡ ¬p
- F와의 XOR연산 결과 : T ⊕ F ≡ T, F ⊕ F ≡ F
- ➜ 원래 명제의 진리값을 그대로 보존.
- p ⊕ F ≡ p
- 명제 자기 자신과의 XOR연산 결과 : 같은 진리값끼리 연산.
- ➜ 항상 F
- p ⊕ p ≡ F
주목해야 할 점.
XOR 연산의 결과에서 원래 명제의 진리값으로 돌아갈 수 있습니다.
어떤 명제에 다른 명제를 두 번 연달아 XOR 연산하게 되면 원래의 결과로 돌아가게 됩니다.
-
명제 p에 q를 XOR 연산하고, 거기에 다시 q를 XOR 연산할 경우 결과
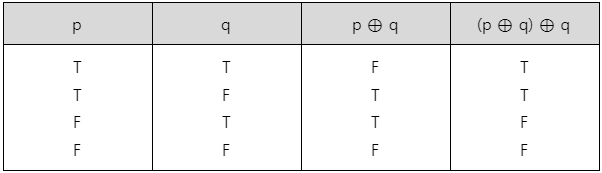
-
(p ⊕ q) ⊕ q ≡ p
이것은 결합법칙으로 간단하게 증명.
- (p ⊕ q) ⊕ q ≡ p ⊕ (q ⊕ q) ≡ p ⊕ F ≡ p
XOR 연산의 이러한 성질은 암호학을 비롯한 컴퓨터과학 분야에서 널리 활용됩니다.
프로그래밍과 논리연산
논리연산자
- 주로 if나 while 문에서 수행 조건을 지정할 때 사용.
- or, and, not로 쓰는 경우(파이썬).
- ||(OR), &&(and), !(NOT)로 쓰는 경우(C++, 자바).
만약 조건문에 참여하는 변수가 많거나 경우의 수가 복잡하다면 연산법칙으로 간략화할 수 있습니다.
ex. if ( (!cond1 || cond2) && !(cond1 && cond2) ) ➜ if ( !cond1 )
XOR는 논리연산보다는 비트단위(bitwise)의 데이터를 조작하는 데 주로 사용. (이때 T, F에 해당하는 것이 1, 0).
ex. 어떤 8비트 데이터를 담고 있는 변수 a의 모든 비트를 반대로 뒤집어 b라는 변수에 할당하는 C++/자바 코드.
a = 0×B5 // 1011 0101, unsigned 8-bit data
b = a ⌃ 0×FF // 1111 1111
// 이제 b는 0×4A(0100 1010)가 됩니다.
0×FF : 모든 비트가 1인 8비트 데이터.
0×FF과 a를 XOR(⌃) 연산해서 b에 담는데, p ⊕ T ≡ ¬p가 되어 부정연산처럼 동작하는 XOR의 성질을 이용한 것.

