게오르크 칸토어 (Georg Cantor, 1845.03.03 ~ 1918.01.06)
: 수학의 본질은 그 자유성에 있다.
이 포스팅은 '수학리부트'를 보며 공부한 내용입니다.
집합
개별적인 개체들의 모임. 대개 영어 대문자로 표시.
원소 : 집합을 이루는 개체. 대개 영어 소문자로 표시.
집합을 이루는 원소들은 중괄호( {} ) 안에 나타냅니다.
어떤 원소가 집합에 속하는지 여부는 ∈기호와 ∉기호로 표시.
- 원소 a가 집합 S에 속한다면 a ∈ S.
- 원소 a가 집합 S에 속하지 않는다면 a ∉ S.
집합의 크기 : 집합에 속한 원소의 개수. ex) 집합 A에 속한 원소의 개수 ➜ | A |
집합의 종류
부분집합 : 어떤 집합의 모든 원소가 다른 집합의 원소이기도 한 경우가 있습니다.
- 집합 A의 모든 원소가 집합 B에도 속할 경우 A는 B의 부분집합. ( A ⊂ B )
- A는 B에 포함된다.
- 부분집합이 아닐 때의 기호 (⊄).
진부분집합 : A ⊂ B이지만 A ≠ B인 경우 즉, B에는 A의 원소가 아닌 것도 포함되어 있을 경우 A는 B의 진부분집합.
원소의 개수에 따라서도 집합을 구분할 수 있습니다.
- 유한집합 ➜ '2보다 크고 10보다 작은 짝수의 집합' 처럼 원소의 개수가 유한할 경우.
- 무한집합 ➜ '자연수 중 3의 배구의 집합' 처럼 무한할 경우.
- 공집합
- 집합에 아무런 원소도 없을 때 ∅
- 공집합 기호 주의에 중괄호를 두르지 않도록 유의해야 합니다. ➜ ∅ ≠ { ∅ }
({∅}은 공집합을 원소로 가지는 집합으로 원소가 아예 없는 공집합과는 같지 않습니다) - 공집합은 그 정의로부터 모든 집합의 부분집합이 됩니다.
상동
A ⊂ B와 B ⊂ A가 동시에 성립한다면 두 집합의 원소는 완전히 동일해야 합니다.
➜ A와 B는 상동 (A = B).
상동의 부정은 기호 ≠
집합의 표현방법
원소나열법
- 말 그대로 집합에 속한 원소들을 일일이 나열하는 방법.
- 원소의 순서는 상관없지만 같은 원소를 중복해서 넣지 않습니다.
- A = { 1, 7, 5, 3, 9 }
- 앞뒤 맥락으로 보아 의미가 분명할 때는 일부 원소들을 생략하고 줄임표로 대신할 수 있습니다.
- B = { 2, 4, 6, ..., 100 } ➜ 2에서 100까지 짝수가 모인 집합.
- B = { 2, 4, 6, ..., 100 } ➜ 2에서 100까지 짝수가 모인 집합.
조건제시법
- 집합의 원소들에 공통되는 조건을 기술하는 방법.
- C = { x | 1 ≤ x ≤ 100 } ➜ 1부터 100까지 자연수의 집합.
- 세로줄 '|' 의 왼쪽에는 원소의 대표 형태, 오른쪽에는 원소가 가져야 할 조건.
벤 다이어그램
- 집합 간의 관계가 복잡하지 않다면 그림으로 나타내는 편이 알아보기 쉽습니다.
- A = {1, 2, 3}이고 B = {2, 4, 6, 8}인 경우
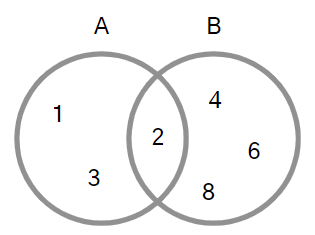
- A = {1, 2, 3}이고 B = {2, 4, 6, 8}인 경우
집합의 연산
합집합 ➜ 집합끼리의 연산을 통해 새로운 집합을 만들기도 합니다.
- 집합 A와 B의 원소들을 합친 것처럼 모두 모은 집합. (A∪B)
- 합집합을 조건제시법으로 나타내면 ➜ A ∪ B = { x | ( x ∈ A ) ∨ ( x ∈ B )}
- 조건 부분에 논리연산 사용.
➜ 합집합의 원소 x가 A에 속한다는 명제(x∈A) 와 B에 속한다는 명제(x∈B)가 논리합(OR)연산으로 연결.
- 조건 부분에 논리연산 사용.
- 위의 벤 다이어그램으로 나타낸 예의 합집합 ➜ A ∪ B = {1, 2, 3, 4, 6, 8}
- 주의) 합집합 A∪B의 크기를 구할 때.
- 두 집합 A와 B의 원소 개수를 단순히 더하면 안되고, 교집합 A∩B에 포함되는 원소들이 양쪽으로 중복하여 계산되기 때문에 교집합의 크기를 빼주어야 합니다. ➜ ( | A ∪ B | = |A| + |B| - | A ∩ B | )
- 두 집합 A와 B의 원소 개수를 단순히 더하면 안되고, 교집합 A∩B에 포함되는 원소들이 양쪽으로 중복하여 계산되기 때문에 교집합의 크기를 빼주어야 합니다. ➜ ( | A ∪ B | = |A| + |B| - | A ∩ B | )
교집합
- 집합 A와 B의 공통된 원소들만 골라낸 집합. (A∩B)
- 교집합을 조건제시법으로 나타내면 ➜ A ∩ B = { x| ( x ∈ A ) ∧ ( x ∈ B )}
- 위의 벤 다이어그램으로 나타낸 예의 교집합 ➜ A ∩ B = {2}
서로소
- 교집합이 ∅인 경우, 두 집합 간에 공통된 원소가 하나도 없는 경우의 두 집합.
- 모든 짝수의 집합 E와 모든 홀수의집합 O는 E∩O = ∅ 이므로 서로소.
여집합 ➜ 때로는 어떤 집합을 제외한 나머지 모든 것을 나타낼 필요가 있습니다.
- ex) '자연수 중 3의 배수가 아닌 수의 집합'
- 우선 '자연수의 집합' 같이 기본 전제가 되는 집합이 정의되어야 함.
➜ 전체집합 (U, Universal Set의 첫글자). - '3의 배수의 집합' 처럼 제외될 집합을 A라 한다면,
- 전체집합 U에서 A를 제외한 것을 A의 여집합. ( Ac )
➜ 어떤집합과 그 여집합을 합치면 전체집합이 되므로, 서로 보완(complement)한다는 뜻 의 c.
- 우선 '자연수의 집합' 같이 기본 전제가 되는 집합이 정의되어야 함.
- Ac = { x | ( x ∉ A ) ∧ ( x ∈ U )}
- 여집합의 여집합 ➜ 부정의 부정 ➜ 자기 자신.
- ( Ac )c = { x | ( x ∉ Ac ) ∧ ( x ∈ U )} = A
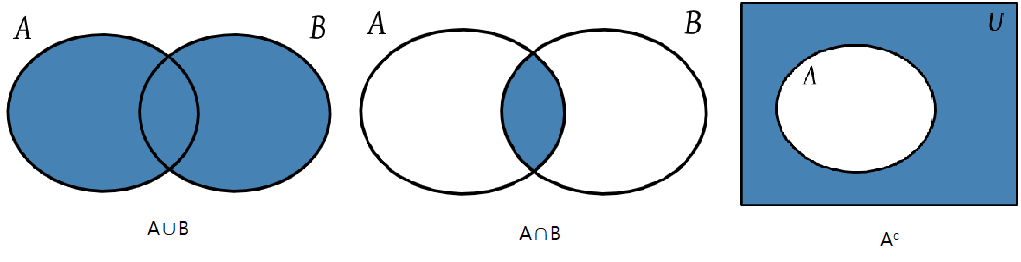
- 전체집합 U에 포함되는 집합 A와 B가 있다고 할 때 합집합·교집합·여집합을 각각 벤다이어그램으로 나타내면
차집합
- 집합 A로 부터 B와 공통인 부분을 제외한(즉, 뺀) 것을 A와 B의 차집합. (A - B)
- 'A이되 B는 아닌 것' ➜ A∩Bc 와 동일.
- A - B = { x| (x ∈ A ) ∧ ( x ∉ B ) } = A ∩ Bc
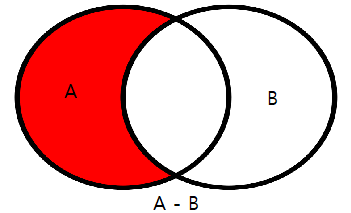
- A - B = { x| (x ∈ A ) ∧ ( x ∉ B ) } = A ∩ Bc
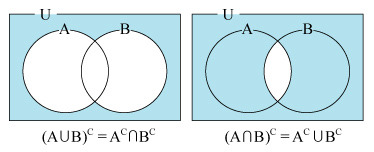
집합의 드 모르간 법칙
합집합이나 교집합 전체에 대해서 여집합을 취하면,
명제에서와 마찬가지로 다음과 같은 집합의 드 모르간 법칙이 성립합니다.
합집합과 교집합을 논리연산으로 정의한 식에 각각 부정(NOT) 연산을 함으로써 유도됨.
- ( A ∪ B )c = { x | ¬( x ∈ A ∨ x ∈ B ) } = { x | ( x ∉ A ) ∧ ( x ∉ B ) } = Ac ∩ Bc
- ( A ∩ B )c = { x | ¬( x ∈ A ∧ x ∈ B ) } = { x | ( x ∉ A ) ∨ ( x ∉ B ) } = Ac ∪ Bc
집합의 연산에서의 교환법칙, 결합법칙, 분배법칙
교환법칙
- 합집합, 교집합 성립 O. (각각 ∨와 ∧만 사용되므로 앞뒤가 바뀌어도 무방)
- B ∪ A = { x | ( x ∈ B ) ∨ ( x ∈ A ) } = A ∪ B
- B ∩ A = { x | ( x ∈ B ) ∧ ( x ∈ A ) } = A ∩ B
- 차집합 성립 X. (앞뒤가 바뀌면 안됨)
- B - A = B ∩ Ac ≠ A ∩ Bc = A - B
- B - A = B ∩ Ac ≠ A ∩ Bc = A - B
결합법칙
- 합집합, 교집합 성립 O.
- ( A ∪ B ) ∪ C = A ∪ ( B ∪ C )
- ( A ∩ B ) ∩ C = A ∩ ( B ∩ C )
- 차집합 성립 X.
- ( A - B ) - C = ( A ∩ Bc ) - C ) = A ∩ Bc ∩ Cc
- A - ( B - C ) = A - ( B ∩ Cc ) = A ∩ ( B ∩ Cc )c = A ∩ ( Bc ∪ C )
분배법칙
- 합집합, 교집합 성립 O.
- A ∪ ( B ∩ C ) = ( A ∪ B ) ∩ ( A ∪ C )
- A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C )
프로그래밍과 집합 자료형의 활용
프로그래밍에서 집합은 중복 없이 데이터를 처리해야 할 때 유용합니다.
다수의 데이터를 한데 모아두기 위해 쓰는 배열(array)이나 리스트(list)같은 자료구조는 그 안에 같은 원소가 있는지 여부에 별로 관심이 없지만, 집합(set) 자료구조는 원소가 중복되지 않음을 보장해줍니다.
ex) 1, 2, 3을 원소로 갖는 A라는 집합에 다시 2라는 원소를 추가했을 때의 결과. (파이썬)
>>> A = {1, 2, 3}
>>> A.add(2)
>>> print(A)
{1, 2, 3}집합 자료형을 지우너하는 언어라면 대부분 합집합, 교집합, 차집합 같은 기본적인 집합 연산도 함께 지원하므로 해당 언어의 설명서를 참고.
