문제
https://www.acmicpc.net/problem/11003
N개의 수 A1, A2, ..., AN과 L이 주어진다.
Di = Ai-L+1 ~ Ai 중의 최솟값이라고 할 때, D에 저장된 수를 출력하는 프로그램을 작성하시오. 이때, i ≤ 0 인 Ai는 무시하고 D를 구해야 한다.
제한 조건
시간 제한: 2.4초
메모리 제한: 512MB
문제 풀이
해당 문제는 특정 구간(Ai-L+1 ~ Ai)에서의 최솟값을 구하는 문제이다.
처음 봤을 때에는 우선순위 큐를 이용하여 문제를 해결하였다.
-> 사실 우선순위 큐로 가능하다고 생각했는데 입력 최댓값이 너무 커서 worst case의 경우에는 해당 시간으로 통과할 수 없었다.
-> 그래서 java11에서 15로 버전업하니 통과 됨. java15라고 그다지 다른 건 없을 텐데 그냥 시간 제한이 제대로 지정되지 않은 것 같다. (내 생각)
- 시간적으로 만족할 수 없는 우선순위 큐를 이용한 방법
- 시간적으로 만족할 수 있는 Deque를 이용한 방법
순으로 설명할 것이다.
PriorityQueue 이용
우선순위 큐를 이용한 아이디어는 간단하다.
- Ai 값을 우선순위 큐에 넣어준다.
이때 우선순위 큐는 입력 값 오름차순을 유지하도록 구현되어 있다. - Di 값을 계산한다.
a. 우선순위에서 peek을 한 Node의 index가 현재 구간을 만족하면 이를 Di로 기재한다.
b. 우선순위에서 peek을 한 Node의 index가 현재 구간을 만족하지 않으면 poll -> 이후 다시 peek을 하여 구간을 만족하는지 확인한다. 이 과정을 반복한다.
해당 방법은 우선순위 큐를 이용하기 때문에 선형 시간이 불가하다.
코드로 나타낸다면,
for(int i=1;i<=N;i++){
queue.add(new Node(i, Integer.parseInt(st.nextToken())));
int start = getStartIndex(i); int end = i;
int value = getMinValue(start, end);
res[i] = value;
}호출하는 메소드의 시간 복잡도를 차치해도
n번 반복하는 반복문 안에서 우선순위 큐에 add를 수행하기 때문에 시간 복잡도가 O(n*logN)이 수행된다.
현재 최악의 n = 5000,000 이니까,
5000,000 * log(5000,000) 수행하면 된다.
계산하면 대충 15*5000,0000인데 내부 메소드랑 여러 수행을 따지면 만족하지 않음 ㅠㅠ 결과적으로 선형 시간을 가져야된다는 걸 알 수 있다.
👇🏻 최솟값을 찾는 내부 메소드 코드이다.
static private int getMinValue(int start, int end){
while(!queue.isEmpty()){
Node now = queue.peek();
if(now.index >= start && now.index<=end){
return now.value;
}
queue.poll();
}
return -1; //실패 경우
}큐에서 가장 작은 값을 확인했을 때 해당 값의 index가 구간 내 값이 아니면 계속 poll()하여 결과적으로, 큐에서 최소값의 경우 최신성을 유지하려는 코드이다.
명확한 시간복잡도를 계산하기가 어려움. 근데 최악의 경우에도 지속적으로 최솟값의 최신성을 유지하기 때문에 큰 시간복잡도가 소요되지 않는다. 그래도 poll()을 수행하기 때문에 각 poll마다 시간복잡도가 O(logN) 소요됨.
Deque 이용
Deque 자료구조는 기존 Queue와 다른 자료구조이다.
https://www.geeksforgeeks.org/difference-between-queue-and-deque-queue-vs-deque/
한마디로 큐의 앞단과 뒷단 모두에서 삽입/삭제/peek이 가능하다. 둘 다 앞 뒤가 아닌 중간에 대해서는 수행할 수 없다. 이것이 큐의 특성.
Deque를 이용하는 이유는 우선순위 큐와 다르게 상수 시간 O(1) 내에 큐를 다룰 수 있기 때문이다. (우선순위 큐의 poll()은 O(logN)임)
이 아이디어 또한 간단하다.
중심 아이디어는, 큐는 항상 최신성, 최소성을 만족해야 한다는 것이다.
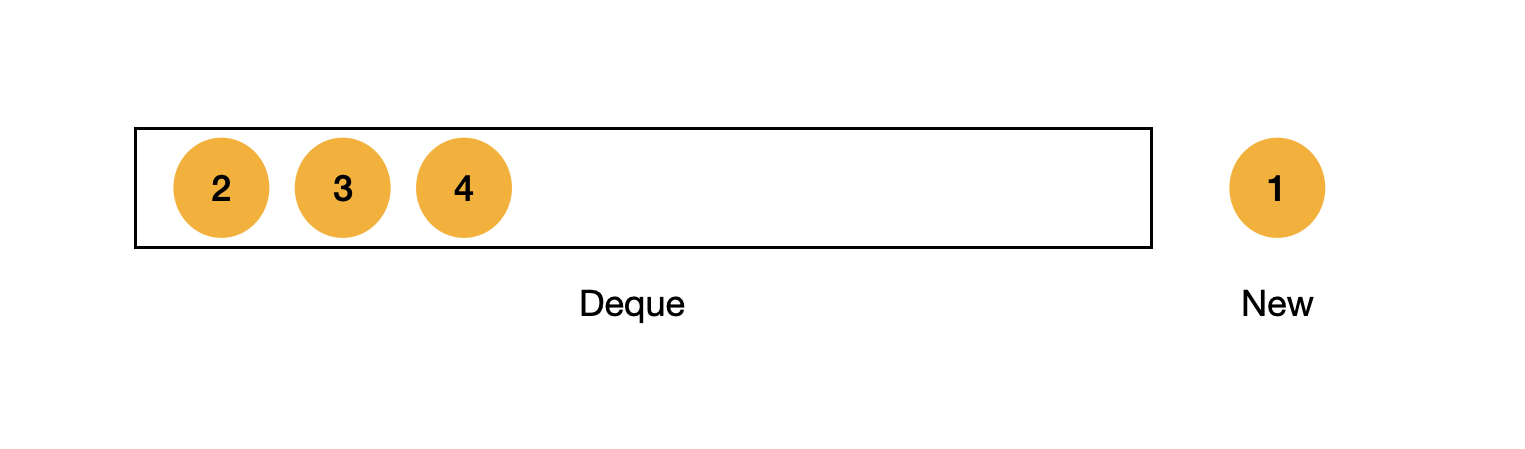
위와 같은 경우를 생각해보자.
1 값을 가진 Ai를 Deque에 넣어야 할 때 이제 큐에 있는 2, 3, 4는 필요가 없다.
Ai+1의 경우에 2, 3, 4 값을 알 필요가 없기 때문이다. 우리가 Deque를 사용하는 이유는 최신 값을 Deque의 앞단에 위치하게 하기 위함이다. 그래서 1값이 상단에 오면 2, 3, 4 값에 접근할 필요가 없다. (이 값들은 오래되었고 작기 때문이다.)
말로 하니까 좀 복잡한데 Ai, Ai+1, Ai+2 등 계속 Ai를 큐에 넣어줄 때 동시에 Di도 같이 구한다고 하면 큐에서 제일 작은 값을 Di로 지정하면 된다. 그렇기 때문에 새로운 값보다 더 작고 오래된 값들은 큐에 유지될 필요가 없다는 것이다.
그래서 새로운 1을 덱에 넣어줄 때,
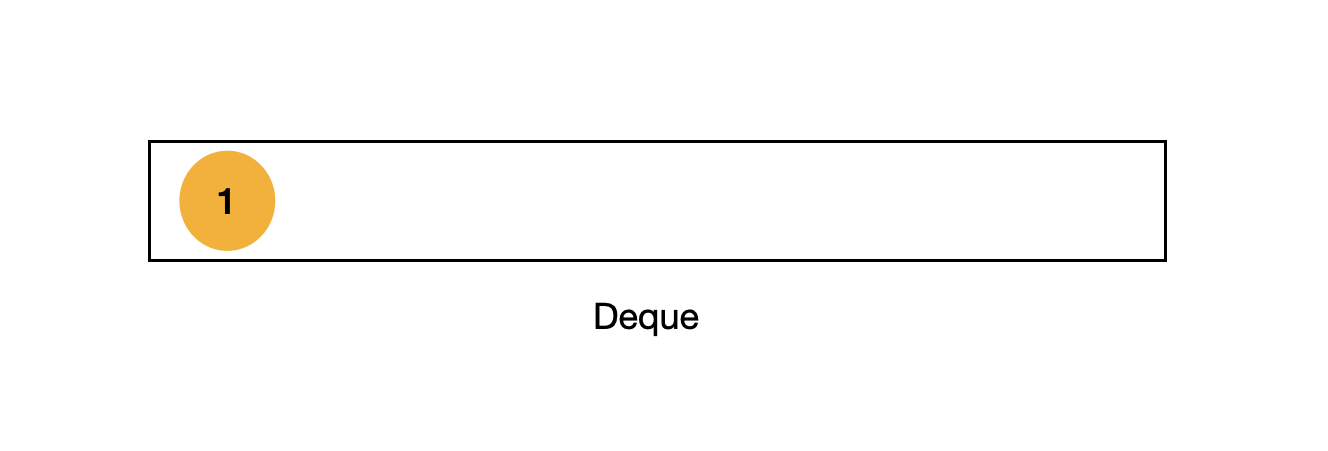
다 제거하고 1만 넣어주면 된다.
이렇게 함으로써 시간복잡도를 줄이고 덱을 항상 최신, 최소성을 만족하도록 한다. <- 이게 덱 풀이에서 가장 중요한 부분이다.
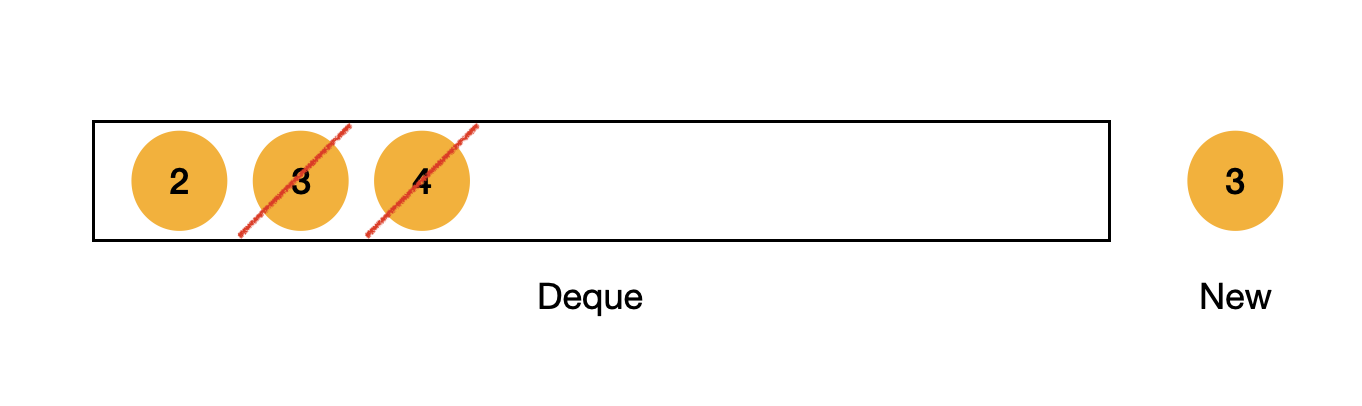
이러한 경우에는 최신성, 최소성을 위해 같거나 큰 수인 3, 4만 제거하고 2는 남긴다.
👍🏻 이렇게 함으로써 덱은 항상 최신, 최소를 유지할 수 있다.
하지만 덱에 넣어줄 때 추가적으로, 고려해야 할 부분이 있다. (안 끝남)
맨 앞에 있는 최솟값이 구간을 만족하지 않는 경우가 있다.
이를 위해 추가적으로 수행해야 하는 것이, 최솟값 구간 확인이다.
L=5인 경우, 1 2 3 2 5 이런 식으로 Ai값이 입력된다고 하면
A6일 때, 덱에는 1 2 5 값이 남을 것이다.
이때 1 값의 경우 A1이기 때문에 구간 값(A2~A6)이 아니다.
이를 위해 매번 덱에 값을 넣어줄 때, 최신 값의 구간 만족을 따지는 로직을 넣어준다. 코드로 확인하면 이와 같다.
private static void insert(Node A){
//queue의 맨 앞은 항상 작고 오래된 거
if(!queue.isEmpty() && queue.peekFirst().index == A.index-L+1-1){
queue.pollFirst();
}
while(!queue.isEmpty()){
if(queue.peekLast().value < A.value){
break;
}
queue.pollLast();
}
queue.addLast(A);
}더 작은 게 나오면 덱에 이 값이 들어갈 때 이전 값들이 삭제되기 때문에 덱의 맨 앞은 항상 작고 오래된 값이 들어가게 된다. 그렇기 때문에 이 로직이 성립된다.
code
Priority Queue
import java.util.*;
import java.io.*;
class Node implements Comparable<Node>{
int index;
int value;
public Node(int index, int value){
this.index = index;
this.value = value;
}
public int compareTo(Node n){
return this.value-n.value;
}
}
class Main{
static int N;
static int L;
static PriorityQueue<Node> queue;
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
L = Integer.parseInt(st.nextToken());
queue = new PriorityQueue<>();
st = new StringTokenizer(br.readLine());
int res[] = new int[N+1];
for(int i=1;i<=N;i++){
queue.add(new Node(i, Integer.parseInt(st.nextToken())));
int start = getStartIndex(i); int end = i;
int value = getMinValue(start, end);
res[i] = value;
}
StringJoiner sj = new StringJoiner(" ");
for(int i=1;i<=N;i++){
sj.add(Integer.toString(res[i]));
}
System.out.println(sj);
}
static private int getMinValue(int start, int end){
while(!queue.isEmpty()){
Node now = queue.peek();
if(now.index >= start && now.index<=end){
return now.value;
}
queue.poll();
}
return -1; //실패 경우
}
static private int getStartIndex(int i){
int res = i-L+1;
if(res<=0){
res = 1;
}
return res;
}
}Deque
import java.util.*;
import java.io.*;
class Node {
int index;
int value;
public Node(int index, int value){
this.index = index;
this.value = value;
}
}
class Main{
static int N;
static int L;
static Deque<Node> queue = new ArrayDeque<>();
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
L = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
int D[] = new int[N+1];
for(int i=1;i<=N;i++){
Node newNode = new Node(i, Integer.parseInt(st.nextToken()));
insert(newNode);
D[i] = queue.peekFirst().value;
}
StringJoiner sj = new StringJoiner(" ");
for(int i=1;i<=N;i++){
sj.add(Integer.toString(D[i]));
}
System.out.println(sj);
}
private static void insert(Node A){
//queue의 맨 앞은 항상 작고 오래된 거
if(!queue.isEmpty() && queue.peekFirst().index == A.index-L+1-1){
queue.pollFirst();
}
while(!queue.isEmpty()){
if(queue.peekLast().value < A.value){
break;
}
queue.pollLast();
}
queue.addLast(A);
}
}