[C++/Algorithm] 트리의 순회

정건희·2024년 11월 28일

C++알고리즘 전위순회 중위순회 트리 후위순회

STL/알고리즘

목록 보기

8/10

1. SWEA 1231 중위순회

문제를 풀기 위해서 기초적으로 갖춰야 하는 지식이다.

문제 내용

주어진 트리를 in-order 형식으로 순회해 각 노드를 읽으면 특정 단어를 알 수 있다.

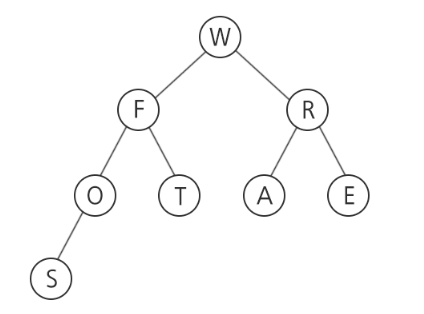
위 트리를 in-order 형식으로 순회할 경우 SOFTWARE 라는 단어를 읽을 수 있다.
주어진 트리를 in-order 형식으로 순회했을때 나오는 단어를 출력하라.

원리

즉, 문제를 풀기 위해서는 다음과 같은 순서로 읽어나가야 한다.

왼쪽 서브 트리를 탐색한다.
루트 노드를 탐색한다.
오른쪽 서브 트리를 탐색한다.

위의 순서를 재귀함수로 구현하면 되는 것..!
코드 형식으로 한 번 보자.
코드는 Chat gpt4 with canvas를 이용하였다. ㅎㅎ

void inorderTraversal(Node* node) {
    if (node == nullptr)
        return;
    inorderTraversal(node->left); // 왼쪽 서브트리 방문
    cout << node->data << " "; // 루트 노드 방문
    inorderTraversal(node->right); // 오른쪽 서브트리 방문
}

풀이

그렇다면 Input단에서부터 확인해 보아요.

1.Input

void input() {
	cin >> N;
	v.resize(N + 1);           // 노드 번호가 1부터 시작하므로 N+1 크기로 벡터 생성
	map.resize(N + 1, { 0, 0 }); // 좌우 자식 정보도 N+1 크기로 생성하여 0으로 초기화
	
	int a, c, d;
	char b;
	//N이 짝수, 홀수냐에 따라 달라짐
	for (int i = 0; i < N; i++) {
		cin >> a >> b;
		v[a] = b;

		if (2 * a <= N) { // 자식이 있는 노드들만 처리 (정점이 2*a로 갈 수 있는지 확인)
			cin >> c;
			map[a].first = c;
			if (2 * a + 1 <= N) { // 오른쪽 자식도 있는 경우
				cin >> d;
				map[a].second = d;
			}
		}
	}
}

2. func

void search(int node) {
	if (node == 0) return; // 노드가 0인 경우 탐색 종료 (자식이 없다는 의미)
	// 좌측 트리 탐색
	search(map[node].first);
	// 현재 노드 탐색
	result += v[node];
	// 우측 트리 탐색
	search(map[node].second);
}

void func() {
	search(1);
}

2. 이진트리의 순회

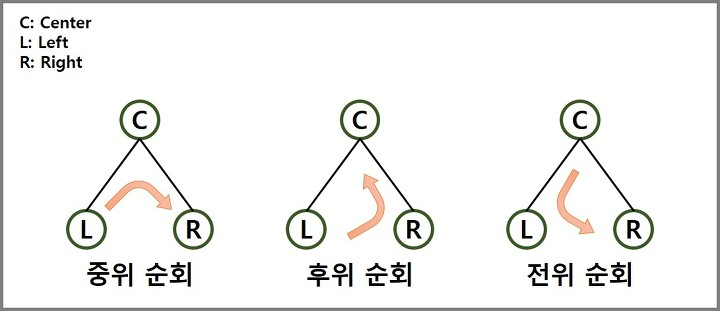
이진 트리의 순회 방법에는 전위 순회(Preorder Traversal), 중위 순회(Inorder Traversal), 후위 순회(Postorder Traversal)의 세 가지가 있습니다. 각 방법은 노드를 방문하는 순서에 따라 구분되며, C++로 구현할 수 있습니다.

1. 전위 순회 (Preorder Traversal)

전위 순회는 루트 노드를 먼저 방문한 후, 왼쪽 자식 노드, 오른쪽 자식 노드의 순서로 방문합니다.

순회 순서: 루트 → 왼쪽 서브트리 → 오른쪽 서브트리

void preorderTraversal(Node* node) {
    if (node == nullptr)
        return;
    cout << node->data << " "; // 루트 노드 방문
    preorderTraversal(node->left); // 왼쪽 서브트리 방문
    preorderTraversal(node->right); // 오른쪽 서브트리 방문
}

2. 중위 순회 (Inorder Traversal)

중위 순회는 왼쪽 자식 노드를 먼저 방문하고, 그 다음에 루트 노드를 방문하며, 마지막으로 오른쪽 자식 노드를 방문합니다.

순회 순서: 왼쪽 서브트리 → 루트 → 오른쪽 서브트리

void inorderTraversal(Node* node) {
    if (node == nullptr)
        return;
    inorderTraversal(node->left); // 왼쪽 서브트리 방문
    cout << node->data << " "; // 루트 노드 방문
    inorderTraversal(node->right); // 오른쪽 서브트리 방문
}

3. 후위 순회 (Postorder Traversal)

후위 순회는 왼쪽 자식 노드와 오른쪽 자식 노드를 먼저 방문한 후, 마지막에 루트 노드를 방문합니다.

순회 순서: 왼쪽 서브트리 → 오른쪽 서브트리 → 루트

void postorderTraversal(Node* node) {
    if (node == nullptr)
        return;
    postorderTraversal(node->left); // 왼쪽 서브트리 방문
    postorderTraversal(node->right); // 오른쪽 서브트리 방문
    cout << node->data << " "; // 루트 노드 방문
}