그래프를 탐색하는 방법에는 너비 우선 탐색(BFS)과 깊이 우선 탐색(DFS)이 있다.
위 링크된 포스팅에서 간단히 언급했었지만, 두 방식의 차이와 언제 어떤 방식을 사용하는지에 대해 면밀히 다뤄보고자 한다.

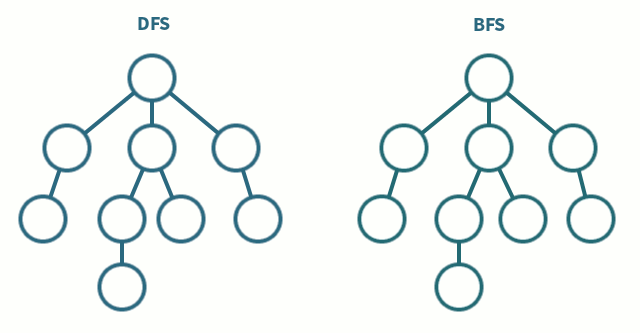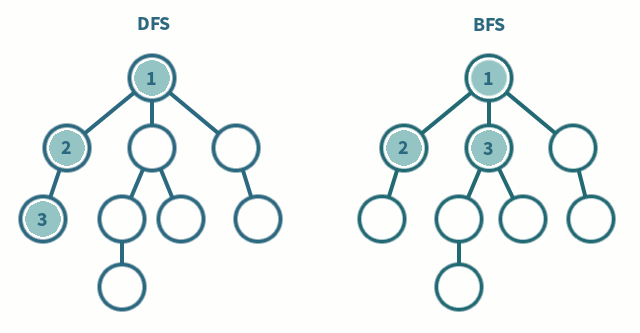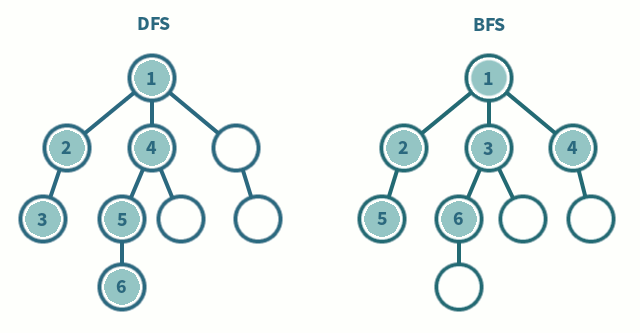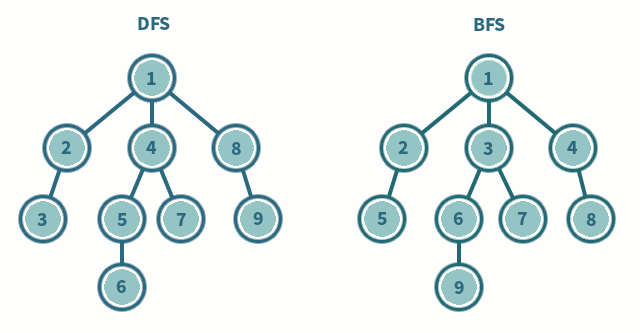
두 알고리즘은 다음과 같이 동작한다.

DFS

• 한 루트로 탐색하다가 특정 상황에서 최대한 깊숙이 들어가서 확인한 뒤 다시 돌아가 다른 루트로 탐색하는 방식
• 재귀, 스택으로 구현
• 백트래킹에도 사용

    static void DFS(int x) {
        visit[x] = true;
        sb.append(x).append(' ');
        for (int y: adj[x]) {
            if (visit[y]) continue;
            DFS(y);
        }
    }

BFS

• 시작 정점의 인접 정점을 순서대로 방문하여 탐색하는 방식
• 큐(Queue)로 구현
• 검색속도는 BFS가 DFS보다 더 빠름

static void BFS(int x) {
        Queue<Integer> q = new LinkedList<>();
        q.add(x);
        visit[x] = true;

        while(!q.isEmpty()) {
            x = q.poll();
            sb.append(x).append(' ');
            for (int y: adj[x]) {
                if (visit[y]) continue;
                q.add(y);
                visit[y] = true;
            }
        }
    }

시간복잡도, 공간복잡도

그래프를 순회하는 시간복잡도는 DFS, BFS 모두 동일하며, 그래프를 저장하는 방식으로 인접 행렬을 사용하냐 인접 리스트를 사용하냐에 따라 차이가 있다.

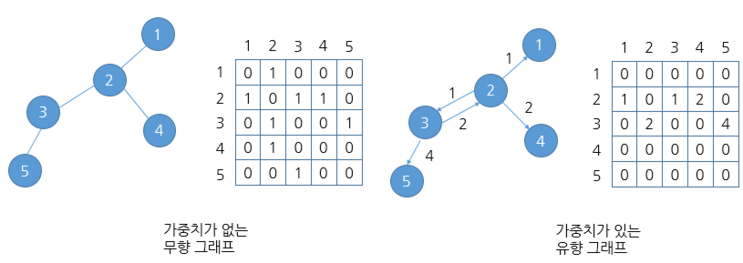
인접 행렬

• 그래프의 연결 관계를 2차원 배열로 나타내는 방식
• 두 정점이 연결됐을 경우 1, 가중치가 있을 경우 가중치로 표현
• 구현이 쉬움
• 차지하는 공간에 비해 사용하는 공간이 굉장이 낮아 활용도가 적음

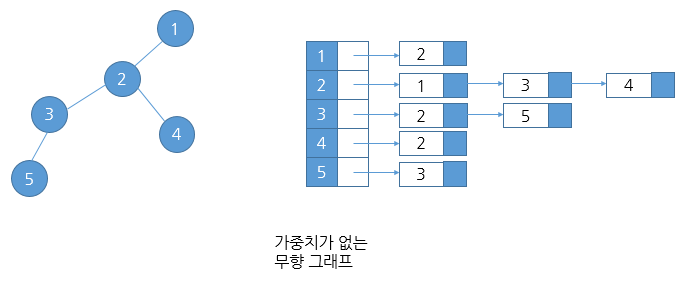
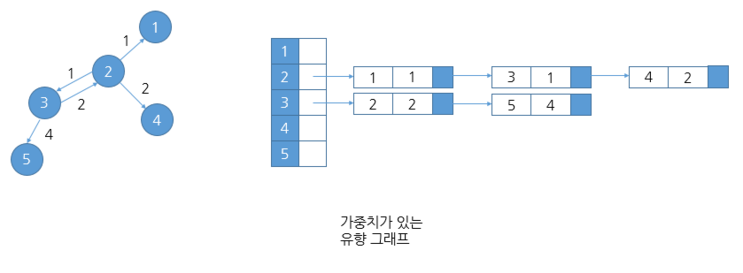
인접 리스트

• 그래프의 연결 관계를 2차원 ArrayList로 나타내는 방식
• 기준 정점과 연결된 정점만을 기록
• 각 정점에 기록된 원소의 수는 해당 정점의 차수와 같음

• 정점 A의 차수(deg(A)) : 정점 A에 연결된 간선의 수
• 모든 정점의 차수의 합 == 모든 간선의 개수 * 2

정점의 개수를 V, 간선의 개수를 E라고 할 때

	인접 행렬	인접 리스트
시간 복잡도	O(V^2)	O(V+E)
공간 복잡도	O(V^2)	O(E)
A->B 연결여부 확인	O(1)	O(min(deg(A), deg(B))), 방향성 그래프는 O(deg(A))
A에 연결된 정점 확인	O(V)	O(deg(A))

• A와 B의 연결 여부 또는 가중치를 확인할 때 인접 행렬은 adj[A][B]로 바로 확인, 인접 리스트는 A의 ArrayList 원소를 모두 확인
• A에서 갈 수 있는 정점을 확인할 경우 인접 행렬은 A행의 모든 열을 확인, 인접 리스트는 A의 ArrayList 원소를 모두 확인

-> 주로 인접리스트를 이용하지만, 연결 여부를 확인하는 경우 인접 행렬을 쓰는 게 시간복잡도가 빠르다. 즉 상황에 따라 사용 방식이 다르므로 두가지 경우를 다 잘 알아두자.
-> 다만, 연결 여부를 확인하는 문제이더라도 간선의 수가 많다면 인접 행렬의 공간복잡도는 O(V^2)로 메모리 초과가 날 수도 있으니 공간복잡도도 반드시 고려할 것!

어떤 상황에 어떤 방식을 적용해야 할까?

DFS

• 각 경로의 특징을 저장해야 할 때
• 그래프의 규모가 클 때 (비교적 공간을 적게 사용함)

BFS

• 두 노드 사이의 최단 경로를 찾고 싶을 때
  (BFS: 기준 노드에서부터 시작하여, 가장 빨리 도착하는 경우가 최단 경로
  <-> DFS: 모든 노드를 다 살펴봐야 함)
• 검색 시작 지점에서부터 찾고자 하는 대상이 멀지 않을 때
  

둘 다 상관 없는 경우

• 그래프의 모든 정점을 방문해야 할 때

출처

https://namu.wiki/w/%EB%84%88%EB%B9%84%20%EC%9A%B0%EC%84%A0%20%ED%83%90%EC%83%89
https://itwiki.kr/w/%EA%B7%B8%EB%9E%98%ED%94%84