예전에 오픈랩 행사를 갔었는데, 교수님들 연구주제들 중에 군집 주행이 종종 등장했었다. 군집이란 단어를 들었었는데, 이게 다른 분야와 연관되어 사용될 수 있는 단어란 것을 알게 되었다.

지도 학습과 달리 레이블이 없는 비지도 학습! 그 중 먼저 군집에 대해 다루어 보려고 한다!

군집? 일단 헤쳐 모여!

데이터 분석, 고객 분류, 추천 시스템, 검색 엔진, 이미지 분할, 준지도 학습, 차원 축소 등에 활용할 수 있는 도구로, 비슷한 샘플을 클러스터로 모은다.

K-평균의 특징?

장점은 너~무 많다. 속도도 빠르지, 확장도 용이하지... 하지만 완벽한 것은 없다!

클러스터의 크기 또는 밀집도가 서로 다르거나 원형이 아닌 경우
😋 작동 잘 안할게~를 시전한다고 함!

군집

군집은 비슷한 샘플을 구별해 하나의 cluster 또는 비슷한 샘플의 그룹으로 할당하는 작업을 의미한다.

분류 역시 샘플을 각 그룹에 할당하지만, 분류는 지도 학습이다.

군집은 어떻게 이용할 수 있을까?

• 고객 분류 → 추천 시스템 만들기 가능
• 데이터 분석 → 군집 분석 선행 후 각 클러스터 분석
• 차원 축소 기법 → 각 클러스터에 대한 샘플의 친화성(affinity)측정 가능
• 특성 공학 → 클러스터 친화성 자체를 추가적인 특성으로 활용 가능
• 이상치 탐지 → 모든 클러스터에 친화성 ↓, 이상치일 확률이 높음!
• 준지도 학습 → 레이블된 샘플이 적다면 군집 후 동일 클러스터에 있는 모든 샘플에 레이블 전파 가능
• 검색 엔진 → 일부 검색 엔진은 제시된 이미지와 비슷한 이미지를 찾아줌
• 이미지 분할 → 이미지에 있는 색상의 수를 줄이면서 물체의 윤곽 감지 용이하게 만듦 → 물체 탐지 및 추적 시스템에 이용

클러스터 감지

• 센트로이드(centroid)라 부르는 특정 포인트를 중심으로 모인 샘플을 찾기
• 샘플이 밀집되어 연속된 영역 찾기

1) k-평균

• k-평균은 반복 몇 번으로 데이터셋을 빠르고 효율적으로 클러스터로 묶어주는 알고리즘
• 1957년 벨 연구소에서 스튜어트 로이드가 펄스 부호 변조 기법으로 제안한 내용, 하지만 1982년에 공개...
• 1965년에 에드워드 포지가 사실상 동일한 알고리즘 발표

그럼 사이좋게 이름 붙이자 : k-평균 = 로이드-포지 알고리즘

k-평균 알고리즘은 센트로이드까지의 거리를 고려하는 것이 전부이기에, 클러스터의 크기가 많이 다르면 잘 작동하지 않음!

→ 따라서 소프트 군집이 유용할 수 있음!

하드 군집 vs 소프트 군집

하드 군집 : 샘플을 하나의 클러스터에 할당
소프트 군집 : 클러스터마다 샘플에 점수를 부여

• 소프트 군집에서 점수는 가우스 방사 기저 함수와 같은 유사도 점수(similarity score) 또는 친화성 점수가 될 수 있다!

근데 이건 어떻게 작동하는 걸까?

👏🏻짠! 센트로이드가 주어졌지롱
모든 샘플에 가장 가까운 센트로이드의 클러스터 할당

👏🏻짠! 샘플의 레이블이 모두 주어졌지롱
각 클러스터에 속한 샘플의 평균 계산 하여 센트로이드 구하기

👏🏻짠 ! 아무것도 없네?

1. 데이터셋에서 k개의 샘플을 뽑아 그 위치를 센트로이드로 지정
2. 샘플에 레이블 할당
3. 센트로이드 업데이트
4. 2,3을 수렴할 때 까지 반복!

😗 그런데 수렴이 언제 끝날 줄 알고...?

→ 샘플과 가장 가까운 센트로이드 사이의 평균 제곱 거리는 각 단계마다 내려갈 수만 있고, 음수가 될 수 없기에 수렴을 보장한다고 함! 따라서 제한된 횟수 안에 수렴하는 것이 보장됨!

🤔 수렴은 보장되지만 적절한 솔루션이 된다고 얘기는 안 했다...

지역 최적점으로 수렴하면 말짱 꽝!

2) 센트로이드 초기화 방법

저 센트로이드 위치 알아요...! 근사지만!!

가자 랜덤~!
랜덤 초기화를 다르게 하여 여러번 알고리즘 실행하여 가장 좋은 솔루션을 선택할 수도 있다.

그런데 최선의 솔루션은 어떻게 찾아야할까?
최선의 솔루션을 보는 성능 지표는 모델의 '이너셔(inertia)`다.
이 값은 각 샘플과 가장 가까운 센트로이드 사이의 제곱 거리 합이다.

k-평균++알고리즘

2006년 논문, by David Arthur & Sergei Vassilvitskii

• 다른 센트로이드와 거리가 먼 센트로이드를 선택하는 초기화 단계를 소개
• 최적의 솔루션으로 수렴할 수 있도록 해주기에 이 과정에서 들어가는 계산은 충분히 할 가치가 있음!

1. 데이터셋에서 랜덤으로 균등하게 하나의 센트로이드 선택 $\bf c^{(1)}$

2. $\frac{D(x^{(i)})^2}{\sum_{j=1}^{n} D(x^{(j)})^2}$

   위의 확률로 샘플 $\bf x^{(1)}$를 새로운 센트로이드 $\bf c^{(1)}$로 선택
   $D(\bf x^{(1)})$ : 샘플 $\bf x^{(1)}$와 이미 선택된 가장 가까운 센트로이드까지 거리
   이 확률 분포 자체는 이미 선택한 센트로이드에서 멀리 떨어진 샘플을 다음 센트로이드로 선택할 가능성을 높임.

3. $k$개의 센트로이드가 선택될 때까지 이전 단계 반복

3) k-평균 속도 개선 & 미니배치 k-평균

2013년 Charles Elkan 논문

"클러스터가 많은 일부 대규모 데이터셋에서 불필요한 거리 계산을 피함으로써 알고리즘의 속도를 상당히 높일 수 있다!"

이용한 것
1. 삼각 부등식(triangle inequality, AC ≤ AB + BC) 사용
(두 점 사이의 직선은 항상 가장 짧은 거리가 된다는 것 이용)
2. 샘플-센트로이드 사이의 거리는 하한선과 상한선 유지

다만❗항상 알고리즘이 훈련 속도를 높이는 것은 아님! 때로는 훈련 속도가 상당히 느려질 수도 있음!

2010년 David Sculley

방식 : 전체 데이터셋을 사용해 반복하지 않고 각 반복마다 미니배치를 사용해 센트로이드를 조금씩 이동

→ 알고리즘의 속도를 3~4배 정도 높이는 것 가능
→ 메모리에 들어가지 않는 대량의 데이터셋에 군집 알고리즘을 적용 가능

특징	일반 K-평균 알고리즘	미니 배치 K-평균 알고리즘
데이터 처리 방식	전체 데이터셋을 한 번에 사용	데이터셋에서 일부 샘플(미니 배치)을 반복적으로 사용
수렴 속도	비교적 느림	더 빠르게 수렴
메모리 사용량	데이터셋 크기에 따라 높음	미니 배치 크기에 따라 낮음
복잡도	데이터 크기에 비례 ((O(n \cdot k \cdot t)))	미니 배치 크기에 비례 ((O(b \cdot k \cdot t)))
결과 품질	일반적으로 더 높은 클러스터링 품질	품질이 다소 낮을 수 있음
적합한 데이터 크기	작은 데이터셋에 적합	대규모 데이터셋에 적합
온라인 학습	지원하지 않음	지원 가능

4) 최적의 클러스터

클러스터 개수는 어떻게 정할까?

가장 작은 inertia를 선택하는 것은?

k ↑ inertia ↓
따라서 k 선택 시 inertia는 좋은 성능 지표가 아님.

클러스터 ↑ 각 샘플은 가까운 센트로이드에 더 가까워져서 inertia 작아짐

그럼 어떻게 정하라고?
"실루엣 점수 silhouette scroe" 이용하자!

정확하지만 계산 비용은 많이 들어간다...등골이 휘어요~

실루엣 점수 : 모든 실루엣 계수의 평균
샘플의 실루엣 계수 :

$a$ : 클러스터 내부의 평균 거리(동일한 클러스터에 있는 다른 샘플까지 평균 거리)
$b$ : 가장 가까운 클러스터까지 평균 거리 (가장 가까운 클러스터의 샘플까지 평균 거리. 샘플과 가장 가까운 클러스터는 자신이 속한 클러스터를 제외하고 b가 최소인 클러스터)

실루엣 계수 범위 : -1~+1

+1에 가까움 : 자신의 클러스터 안에 잘 속해 있지만, 다른 클러스터와는 멀리 떨어져 있음.
0에 가까움 : 클러스터 경계에 위치
-1에 가까움 : 샘플이 잘못된 클러스터에 할당

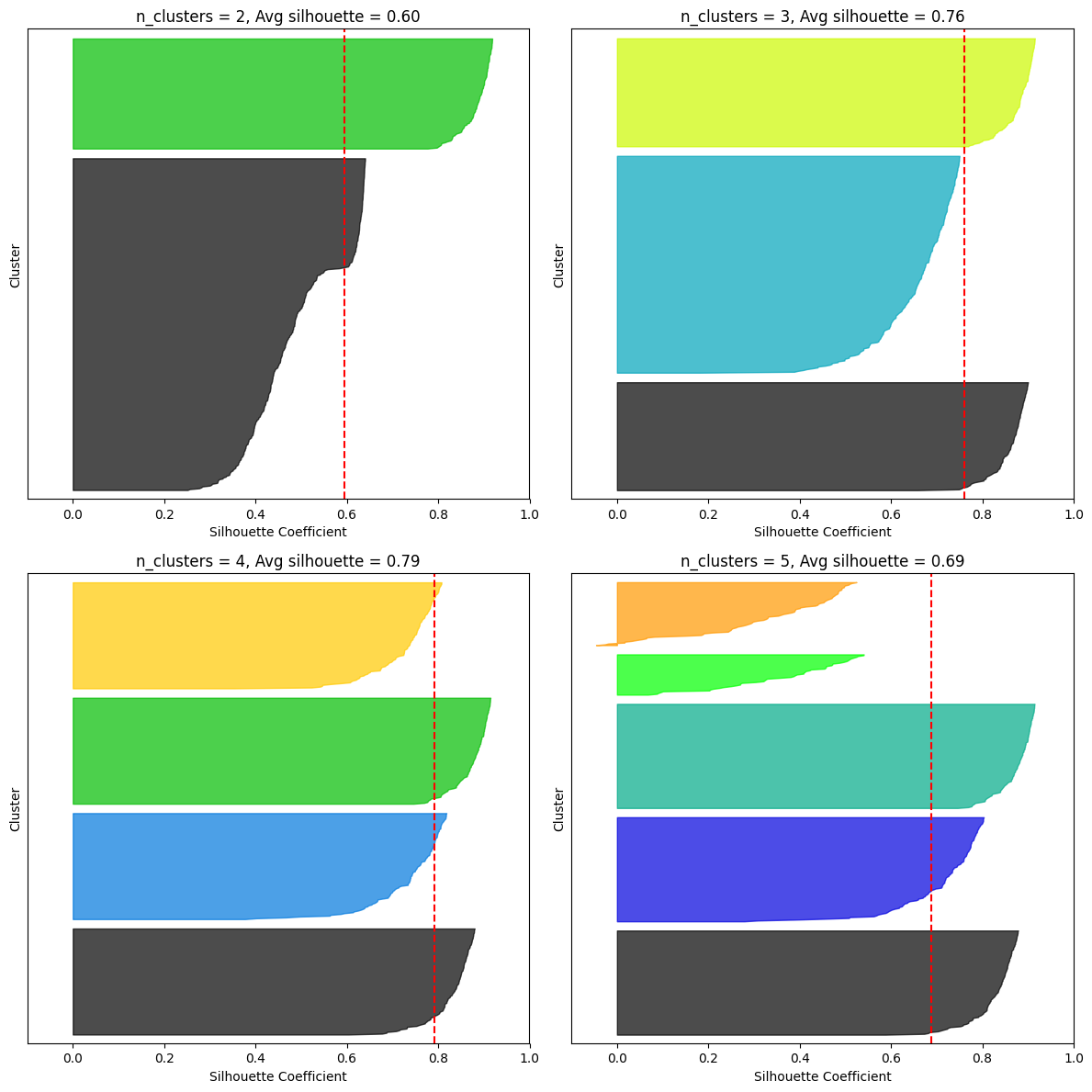
모든 샘플의 실루엣 계수를 할당된 클러스터와 계수 값으로 정렬하여 그리면 더 많은 정보를 얻을 수 있는데, 이게 바로 실루엣 다이어그램(silhouette diagram)

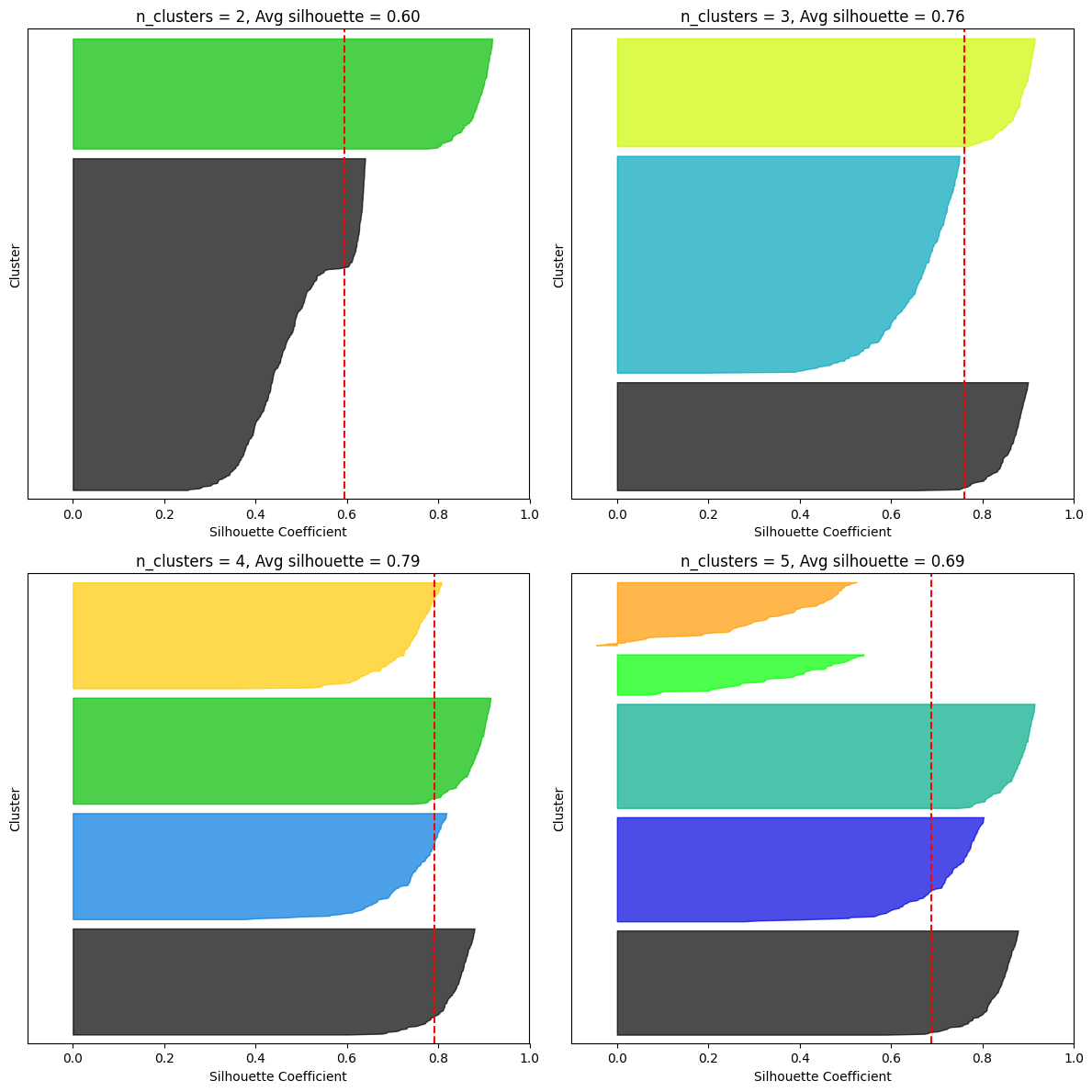
그래프 높이 : 클러스터가 포함하고 있는 샘플의 개수
그래프 너비 : 클러스터에 포함된 샘플의 정렬된 실루엣 계수(넓을수록 좋음)
수직 파선 : 각 클러스터 개수에 해당하는 평균 실루엣 점수

• 많은 샘플이 파선의 왼쪽에서 멈추면 나쁜 클러스터
  - 왜? 클러스터 샘플이 다른 클러스터랑 너무 가깝다는 뜻이니!

5) 군집을 이용한 이미지 분할

이미지 분할(image segmentation) = 이미지를 여러 개의 segment로 분할

• 색상 분할
• 시맨틱 분할
• 인스턴스 분할

시맨틱 분할과 인스턴스 분할에서 최고 수준의 성능을 내려면 CNN 기반의 복잡한 모델을 사용하는 것이 좋다!

특징	색상 분할	시맨틱 분할	인스턴스 분할
목적	색상 기반으로 영역 분리	클래스별로 픽셀 레이블링	개별 객체를 픽셀 단위로 구분
기술적 난이도	쉬움	중간	어려움
결과	특정 색상 영역 마스크 생성	클래스별 분할된 이미지	객체별로 분리된 이미지
모델	간단한 임계값 계산	U-Net, DeepLab 등	Mask R-CNN, SOLO 등
응용 분야	간단한 객체 탐지	자율 주행, 의료 영상	AR/VR, 로봇 비전

k- 평균은 비슷한 크기의 클러스터를 만드는 경향이 있음.
→ 아무리 화려한 무늬를 가지더라도 k-평균이 하나의 클러스터로 만들지 못함.

6) 군집을 이용한 준지도 학습

사실상 전처리 하는 것이다!

😗 언제 사용하지?
→ 레이블이 없는 데이터가 많고 레이블이 있는 데이터는 적을 때!

대표 이미지 : (representative image) 각 클러스터에서 센트로이드에 가장 가까운 이미지 찾기, 여기서 이 이미지가 대표 이미지

레이블 전파 : (label propagation) 랜덤 샘플대신 대표샘플에 레이블을 할당

클러스터 중심에서 먼 샘플 제거 : 일부 이상치 제거 → 정확도 향상

능동 학습(active learning) - 불확실성 샘플링(uncertainty sampling)

능동 학습 : 전문가가 학습 알고리즘과 상호 작용하여 알고리즘이 요청할 때 특정 샘플의 레이블을 제공

<불확실성 샘플링 작동 방식>
1. 지금까지 수집한 레이블된 샘플에서 모델을 훈련, 이 모델을 사용해 레이블되지 않은 모든 샘플에 대한 예측을 만들기
2, 모델이 가장 불확실하게 예측한 샘플(즉, 추정 확률이 낮은 샘플)을 전문가에게 보내 레이블을 붙이기
3 레이블을 부여하는 노력만큼의 성능이 항상되지 않을 때까지 이를 반복

다른 전략 : 모델을 가장 크게 바꾸는 샘플이나 모델의 검증 점수를 가장 크게 떨어뜨리는 샘플, 여러 개의 모델이 동일한 예측을 내지 않는 샘플에 대해 레이블 요청

7) DBSCAN

density-based spatial clustering of applications with noise

여기서 클러스터 : 밀집된 연속적 지역

1. 알고리즘이 각 샘플에서 작은 거리인 ε 내에 샘플이 몇 개 놓여 있는지 세기
   a. 이 지역을 샘플의 ε-이웃 (ε-neighborhood)라고 부름
2. 자기 자신을 포함해 ε-이웃 내에 적어도 min_samples개의 샘플이 있다면 이를 핵심 샘플(core instance)로 간주 → 즉 핵심 샘플 = 밀집된 지역에 있는 샘플
3. 핵심 샘플의 이웃에 있는 모든 샘플 → 동일한 클러스터 (이 방법으로 하나의 클러스터 생성)
4. 핵심 샘플X, 이웃 샘플 X → 이상치

• 모든 클러스터가 밀집되지 않은 지역과 구분될 때 좋은 성능 가능!
• 클러스터 모양과 개수에 상관없이 사용 가능
• 이상치에 안정적, 매개변수 2개(eps, min_samples)
• 클러스터 간의 밀집도가 크게 다르거나, 일부 클러스터 주변에 저밀도 영역이 충분히 없는 경우엔 클러스터 올바르게 잡기에 어려움 있을 수 있음.
• 계산 복잡도 : $O(m^2n)$ → 대규모 데이터셋 확장 잘 X

8) 다른 군집 알고리즘

병합 군집

agglomerative clustering

반복마다 인접한 클러스터 쌍을 연결하여 트리를 만드는데,
이때 트리는 이진 트리가 된다. (트리의 leaf = 개별 샘플)

• 다양한 형태의 클러스터 감지 가능
• 특정 클러스터 개수 선택에 도움이 되는 유용한 클러스터 트리 만들기 가능
• 짝 거리(pairwise distance)와도 사용 가능
• 이웃한 샘플 간의 거리를 담은 $m \times m$ 크기 희소 행렬을 연결 행렬로 전달하는 식으로 대규모 샘플에도 적용 가능

단! 연결 행렬이 없으면 대규모 데이터셋으로 확장하기 어려움!

BIRCH

balanced iterative reducing and clustering using hierarchies

• 대규모 데이터셋을 위해 고안됨.
• 특성 개수가 너무 많지 않으면(20개 이하, 오 적은데) 배치 k-평균보다 빠르고 비슷한 결과를 만듦
• 훈련 과정에서 새로운 샘플을 클러스터에 빠르게 할당할 수 있는 정보를 담은 트리 구조를 만드는데, 이 트리에 모든 샘플을 저장하지는 않는다.
• 제한된 메모리를 사용하기에 대용량 데이터셋 다루기 가능

평균-이동

1. 각 샘플을 중심으로 하는 원 그리기
2. 원마다 안에 포함된 샘플의 평균 구하기
3. 원의 중심을 평균점으로 이동

→ 모든 원이 이동하지 않을 때까지 이러한 평균-이동(mean-shift) 반복

• 동일한 지역에 안착한 원에 있는 모든 샘플은 동일한 클러스터가 됨!
• DBSCAN과 유사한 특징이 있으나, 모양이나 개수 상관없이 클러스터 찾기 가능!
• 하이퍼파라미터 : 대역폭(bandwidth, 원 반경) 1개뿐! → 국부적인 밀집도 추정에 의존
• 클러스터 내부 밀집도가 불균형 → 클러스터를 여러 개로 나누느 경향 있음
• 계산 복잡도 : $O(m^2)$ → 대규모 데이터셋에 적합 X

유사도-전파

예시(exemplar)
이해가 안 가니까 예시로 기억하자...!

정치적인 상황에서는 나와 비슷한 의견을 가진 후보에게 투표하고 싶지만, 해당 당이 이기는 것이 더 우선이기에 더 인기 있는 후보를 선택할 수도 있다.

모든 샘플은 자신을 대표할 다른 샘플(데이터는 정치가 아니니까 자신도 포함!)을 ㅅ헌택할 때까지 샘플 간에 메시지를 반복적으로 교환하며, 이렇게 선출된 샘플이 예시다.

k-평균과 달리 미리 클러스터 수를 정할 필요가 없다. 훈련 중에 결정되기 때문이다. 하지만 k-평균과 유사하게 클러스터의 중심 근처에 위치한 예시를 선택하는 경향도 있다.

다양한 크기의 데이터 처리가 가능하지만, 계산 복잡도가 $O(m^2)$이라 대규모 데이터셋엔 적합하지 않다!

스펙트럼-군집

샘플 사이의 유사도 행렬을 받아서 저차원 임베딩 생성(행렬의 차원 축소)
→ 이 저차원 공간에서 또 다른 군집 알고리즘 사용(사이킷런은 k-평균 이용)

• 복잡한 클러스터 구조 감지 가능
• 그래프 컷(graph cut) 찾는 데 이용 가능(=소셜 네트워크에서 친구의 클러스터 찾기 가능)