Survival Analysis in R _ 01. Introduction to Survival Analysis

01. What is survival data?

• 생존데이터는 사건이 발생할 때까지의 시간 구간을 측정한 데이터이다.
• ex) Time to surgery to death, Time from start of treatment to progression, Time from response to recurrence
• 생존분석은 의학 통계 뿐만 아니라 다양한 영역에서 사용되고 있다. 아래와 같은 이름으로도 불리운다.
• Reliability analysis, Duration analysis, Event history analysis, Time-to-event analysis

02. What is censoring?

• censoring(중도절단)은 다양한 이유로 발생한다. 중도 탈락, 연구 참여 철회, 연구 기간동안 이벤트가 발생하지 않는 경우 등.
• censoring은 생존 분석에서 가장 중요한 개념이다. 크게 두 가지로 나눠서 생각할 수 있다.
• right censoring : 관찰 기간 보다 event 발생 시각이 느린 경우. 주로 censoring은 right censoring을 의미한다. right censoring은 연구 종료, 타겟 이벤트가 아닌 다른 이유로 사망, 중도 탈락 등으로 발생한다.
• left censoring : 관찰 기간보다 event 발생 시각이 빠른 경우.

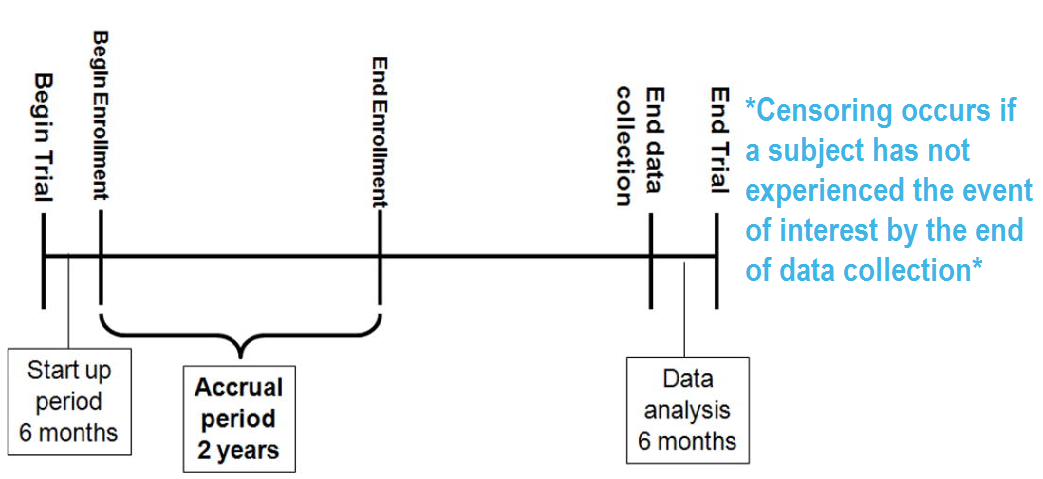
RICH JT, NEELY JG, PANIELLO RC, VOELKER CCJ, NUSSENBAUM B, WANG EW. A PRACTICAL GUIDE TO UNDERSTANDING KAPLAN-MEIER CURVES. Otolaryngology head and neck surgery: official journal of American Academy of Otolaryngology Head and Neck Surgery. 2010;143(3):331-336. doi:10.1016/j.otohns.2010.05.007.

• censoring 데이터 또한 분석에 중요한 재료로 쓰인다. 사용 가능한 특정 시점($t$)을 파악한 후 분석에 활용하는 것이 생존분석이 중요한 이유다.
• 특정 시점($t$)를 파악하기 위해 각 그룹 별 시간 분포도를 확인할 필요 있다.

03. Components of survival data

• $Ti$ : 사건 발생 시간

• $Ci$ : censoring (중도절단) 발생 시간

• Ovserved time $Yi$ = min($Ti$, $Ci$), 관측시간

• Event indicator (중도절단여부, censoring indicator)
  -> 1 : $Ti$ $\leq$ $Ci$
  -> 0 : $Ti$ $>$ $Ci$

• 즉, 데이터는 $(y_1,d_1), (y_2, d_2), (y_3, d_3) ...(y_n, d_n)$ 형태를 띄게 된다. 여기에서 $y_1$는 $d_1$ = $0$ 이면 censoring time, $d_1$ =$1$ 이면 survival time을 의미한다.

04. Survival probablily

• $T$ : 환자의 생존시간
• $t$ : 특정 시간
• $S(t)$ = $P$($T$ $>$ $t$) : 특정 시점t에서 살아 있을 확률.
• $F(t)$ = $1 - S(t)$ = $P$($T$ $\leq$ $t$) : 특정시점 t까지 event가 발생했을 확률.(누적분포함수)
• f($t$) = F$'$($t$) : 특정 시점 $t$에서 event가 발생할 확률. $F(t)$의 $t$에 대한 미분이다.
• 생존함수는 아래와 같은 성질을 갖고 있다.
• $S(0) = 1$, $S(\infin) = 0$
• $S(t_1)$ $\geq$ $S(t_2)$ , $t_1$ $<$ $t_2$ 단조감소

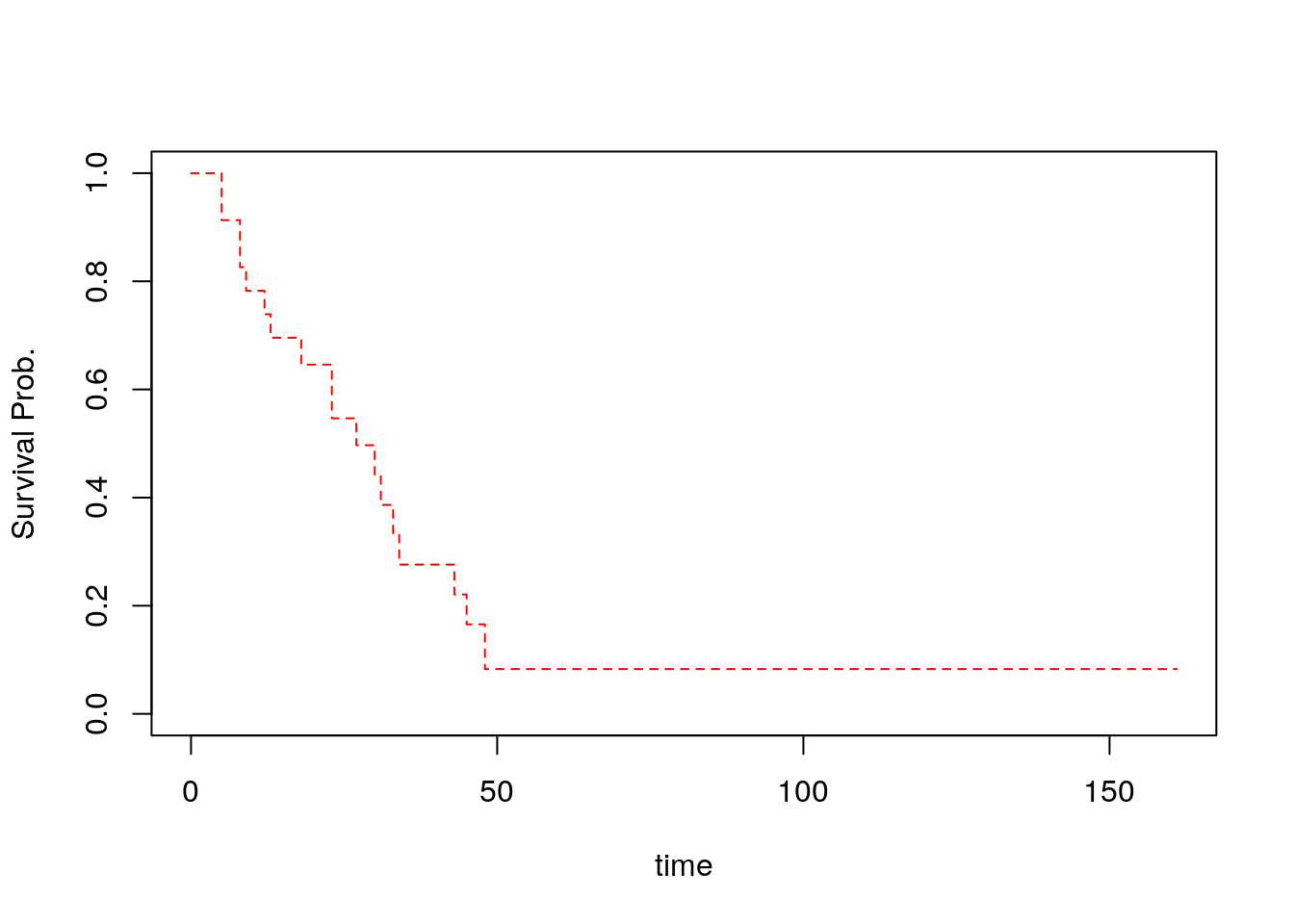
• censoring 데이터로 인해 마지막 시점에서 0이 아닐 수도 있다.
• 위 그림에 따르면, 연구 종료까지 환자 중 10%는 event가 발생하지 않았다.

05. Kaplan-Meier method(누적 한계 추정법)

• censoring이 있는 데이터에서 생존 함수를 추정하는 대표적인 비모수적인 방법.

• 비모수 : 데이터가 정규분포가 아니며 데이터의 표본 수가 적거나 부족하고 데이터가 서로 독립적인 경우.

• 전체 관측시간 데이터를 순서대로 정렬한 후 각 사건의 발생시점의 생존률을 계산하는 방식. 즉,censoring이 있을 때, 그 사람이 t시점까지 살았다는 것을 활용하여 각 시점에서 survival rate을 구하여 계속 곱하면서 생존 함수를 추정한다.
  

06. The Cox regression model(Cox의 비례위험 회귀모형_준모수적 방법)

• 시간과 사건(Event) 사이의 예측 회귀 모형을 만드는 통계법으로, KM method는 타겟하는 특성 외의 다른 요인들을 통제할 수 없는 것에 반해, Cox 비례위험모형은 다양한 관측치들에 대해 사건 발생에 미치는 영향을 분석하는 다변량 분석법임.

• Cox 모형의 결과는 HR(Hazard Ratio, 위험비율)로 해석함. 비례 가정이 만족되지 않을 경우 time dependent covariate approach.

• 위험 함수 (Hazard Function) : t 시점까지는 생존했다고 가정하고 바로 직후 사망할 확률.
  

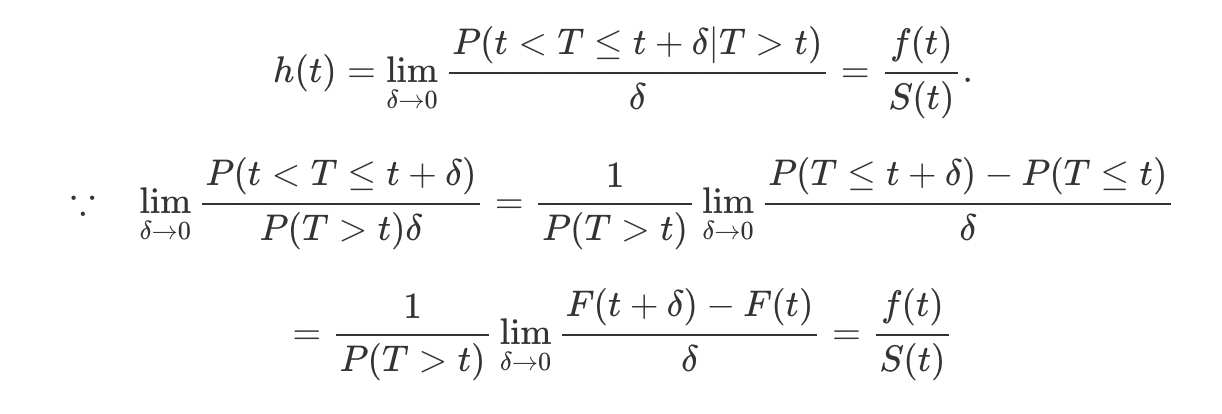
• 생존시간 $T$에 영향을 주는 변수(공변량)들 $x_1$, $x_2$, $x_3$, .... , $x_p$ 가 존재할 때, 위험함수는 다음과 같다.

• $h(t)$ = $h_0(t)$ $exp(\beta_1x_1$+ ... + $\beta_px_p)$

• $log$ $h(t)$ = $log$ $h_0(t)$ + $\beta_1 x_1 +... + \beta_p x_p$

• $h_0(t)$ = baseline hazard, 즉, 모든 $x$들이 0일 때의 위험 함수

• Hazard Ratio (위험비율) : 특정 시점(t)에서 두 그룹간의 위험 비율을 의미.

• HR $>$ 1 : 사망 위험 증가

• HR $<$ 1 : 사망 위험 감소

• ex)

• 남자 : $log$ $h$$($t$|x_1 = 1)$ = $log$ $h_0(t)$ + $\beta_1 + \beta_2x_2+...+\beta_px_p$

• 여자 : $log$ $h$$($t$|x_1 = 0)$ = $log$ $h_0(t)$ + $\beta_2x_2+...+\beta_px_p$

• 두 로그위험함수식의 차를 구하면 회귀계수($\beta_1$)과 일치함.

• Hazard ratio : $\frac {h(t|x_1 = 1)}{h(t|x_1 = 1)}$ = e$^{\beta_1}$

07. R 실습

# library
library(survival)
library(survminer)
library(lubridate)
library(tidyverse)

# data 
date_ex <- 
  tibble(
    sx_date = c("2007-06-22", "2004-02-13", "2010-10-27"), 
    last_fup_date = c("2017-04-15", "2018-07-04", "2016-10-31")
    )

date_ex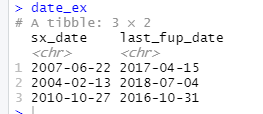

# Formatting dates
# base R
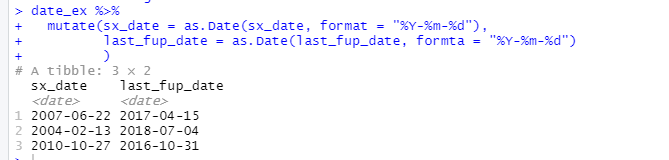
date_ex %>% 
  mutate(
    sx_date = as.Date(sx_date, format = "%Y-%m-%d"), 
    last_fup_date = as.Date(last_fup_date, format = "%Y-%m-%d") 
    )
      
# Lubridate package
date_ex %>% 
  mutate(
    sx_date = ymd(sx_date), 
    last_fup_date = ymd(last_fup_date)
    )

• 데이터 형태가 정형화 되어 있으면 lubridate, 데이터 형태가 비정형 상태면 base R 사용!

# Calculating survival times 
# base R
date_ex %>% 
  mutate(
    os_yrs = 
      as.numeric(
        difftime(last_fup_date, 
                 sx_date, 
                 units = "days")) / 365.25
    )
# lubridate package
date_ex %>% 
  mutate(
    os_yrs = 
      as.duration(sx_date %--% last_fup_date) / dyears(1)
    )

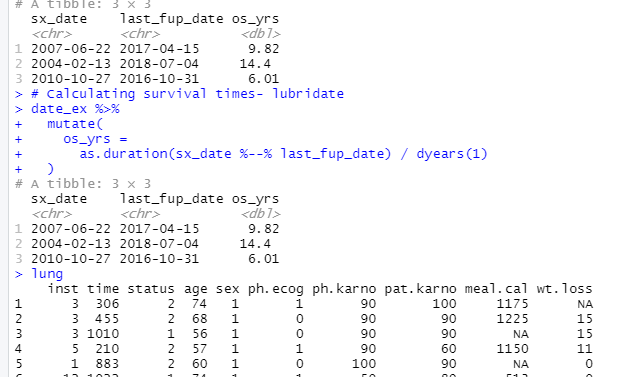
# Creating survival objects
Surv(lung$time, lung$status)[1:10]

# Estimating survival curves with the Kaplan-Meier method
f1 <- survfit(Surv(time, status) ~ 1, data = lung)
names(f1)

# Kaplan-Meier plot 
# base R
plot(survfit(Surv(time, status) ~ 1, data = lung), 
     xlab = "Days", 
     ylab = "Overall survival probability")
     
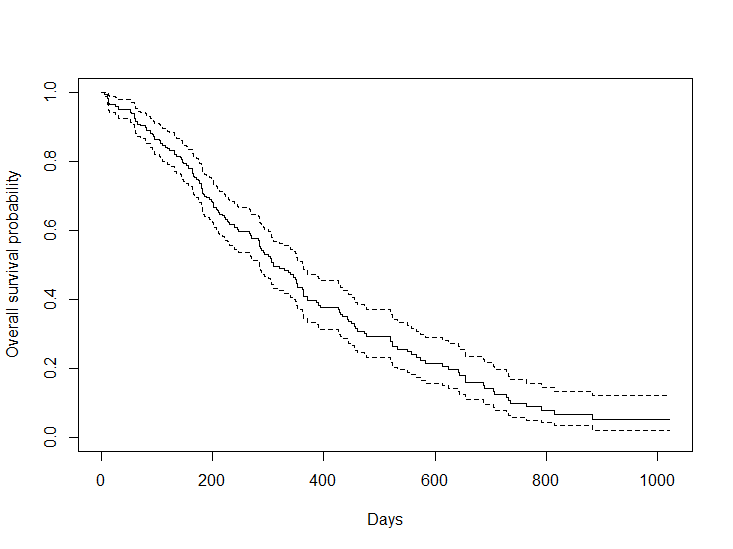
# ggsurvplot
ggsurvplot(
    fit = survfit(Surv(time, status) ~ 1, data = lung), 
    xlab = "Days", 
    ylab = "Overall survival probability")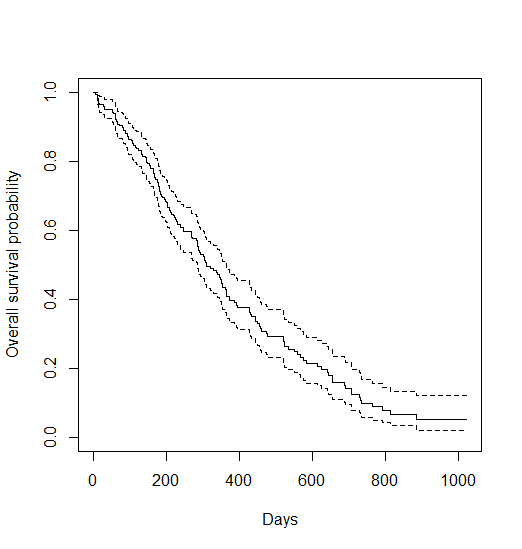

# Estimating x-year survival
summary(survfit(Surv(time, status) ~ 1, data = lung), times = 365.25)

# Estimating median survival time 
survfit(Surv(time, status) ~ 1, data = lung)

# Median survival is often estimated incorrectly
lung %>% 
  filter(status == 2) %>% 
  summarize(median_surv = median(time))

# Comparing survival times between groups
survdiff(Surv(time, status) ~ sex, data = lung)

# Extracting information from a survdiff object
sd <- survdiff(Surv(time, status) ~ sex, data = lung)
1 - pchisq(sd$chisq, length(sd$n) - 1)+

ezfun::sdp(sd)

# The Cox regression model
coxph(Surv(time, status) ~ sex, data = lung)

# Formatting Cox regression results
broom::tidy(
  coxph(Surv(time, status) ~ sex, data = lung), 
  exp = TRUE
  ) %>% 
  kable()
  
 coxph(Surv(time, status) ~ sex, data = lung) %>% 
  gtsummary::tbl_regression(exp = TRUE) 

참고자료

• http://bigdata.dongguk.ac.kr/lectures/med_stat/_book/%EC%83%9D%EC%A1%B4%EB%B6%84%EC%84%9D-survival-analysis.html
• https://www.emilyzabor.com/tutorials/survival_analysis_in_r_tutorial.html#Part_1:_Introduction_to_Survival_Analysis

https://m.blog.naver.com/kunyoung90/222037025576