Hands-On Machine Learning with Scikit-Learn and TensorFlow 책을 공부하고 내용을 정리한 글이다.
Linear Regression
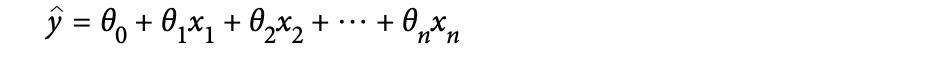
위의 식은 선형회귀 예측 모델 식으로 벡터로도 표현이 가능하다. 상수항을 포함하여 모델 파라미터를 벡터로 한 번에 표현한다.
모델을 학습시킬 때는, RMSE를 최소화하는 파라미터 벡터를 찾으면 된다.
RMSE보다 MSE를 구하는 것이 더 쉽기 때문에 주로 MSE를 평가지표로 활용한다. (결과는 RMSE나 MSE로 구하는 것이나 동일하다.)
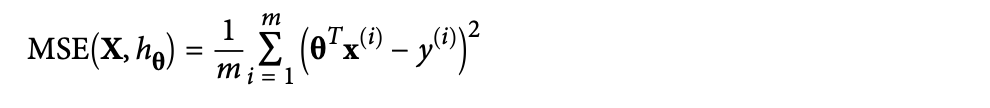
위의 과정 없이 바로 최적의 파라미터 해를 구할 수 있는 공식도 존재한다. 이는 Normal Equality라고 부른다. (X의 역행렬이 존재할 때만 사용 가능하다.)

파이썬에서 위의 공식을 활용하여 직접 계산하여 구할 수도 있고, from sklearn.linear_model import LinearRegression를 이용하여 구할 수도 있다.
SVD를 활용하여 X를 세 개의 행렬로 분해하여 해를 구할 수도 있다.
Gradient Descent
만약 feature의 수가 많거나 학습시켜야 할 데이터가 방대하다면, Gradient Descent가 최적의 알고리즘이 될 것이다.
최적의 파라미터를 찾기 위해 loss function을 계산할 때, 가장 크게 loss function을 줄이는 방향으로 계속해서 나아가는 것이다. 최종적으로 기울기가 0이 될 때, 학습을 종료한다. (가장 minimum에 도달했다는 의미)
minimum에 수렴할 때까지 계속해서 학습을 반복하고, 초기 값은 random으로 결정한다.(random initialization)
각 학습의 사이즈를 결정하는 learning rate이라는 하이퍼파라미터가 가장 중요하다. 너무 작지도, 크지도 않게 결정한다.
만약 minimum이 2개 이상이라면? (local minimum & global minimum)
시간은 좀 걸릴지라도 결국엔 global minimum을 찾아낼 것이다.
Batch Gradient Descent
Gradient Descent를 사용한다는 것은 조금이라도 방향이 바뀐다면 그때마다 파라미터별 MSE를 계산해야 하는 것과 동일한 의미이다.
아래의 식을 활용하면 한꺼번에 계산할 수 있게 된다.
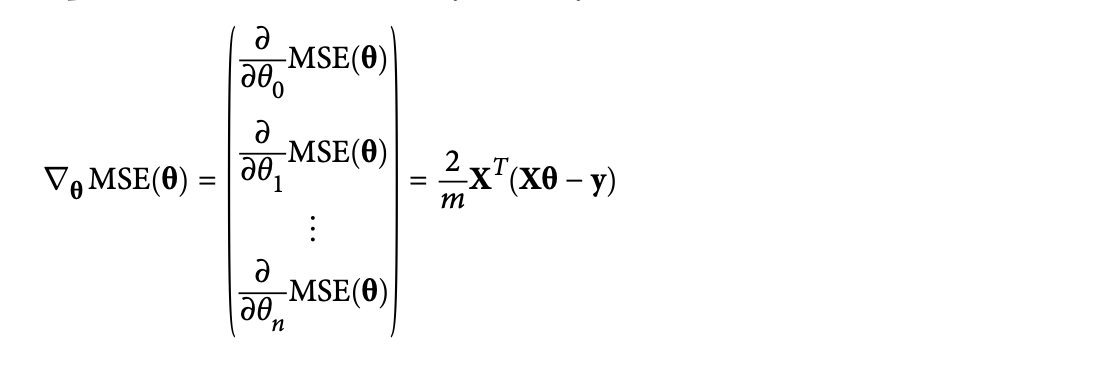
만약 gradient vector를 구했다면, 다음 단계는 그 반대 방향으로 학습을 진행하면 된다. (아래의 식에서 뺄셈이 이를 의미)

학습의 횟수를 지정한 채 학습을 진행할 수 있다. 수렴하기까지 너무 오래걸리거나 너무 빨리 수렴하여 추가적으로 진행하는 학습이 쓸모 없을 경우 낭비를 줄이기 위해 number of iterations를 지정한다.
Stochastic Gradient Descent
Batch Gradient Descent의 단점은 매 단계 학습할 때마다 전체 학습 데이터를 사용한다는 것이다. (속도 저하의 원인)
이와 반대로 Stochastic Gradient Descent는 각 학습 단계마다 랜덤하게 데이터를 지정하여 학습을 진행한다. (stochastic = random)
대신 학습 단계를 진행할 때, Gradient Descent보다는 수렴할 때, bounce가 더 많이 될 것이다. (아래의 사진에서 일직선으로 진행되지 않는 것을 확인할 수 있음)
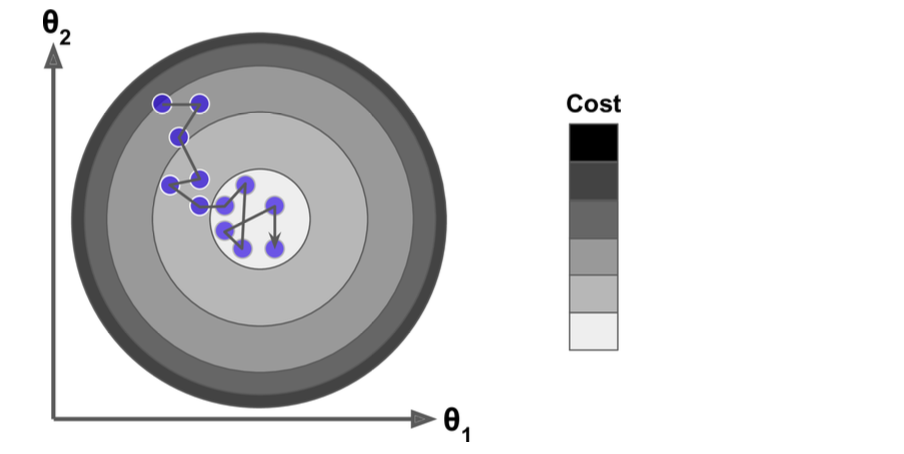
randomness 개념이 도입되기 때문에 minimum에 도달하지 못할 수 있다. 그렇기 때문에 learning rate를 점점 줄여나가며 학습을 진행하는 방법을 활용한다.
파이썬에서 선형 회귀에서 Gradient Descent를 활용하려면, from sklearn.linear_model import SGDRegressor를 사용한다.
Polynomial Regression
파이썬에서 다중회귀를 하기 위해서는 from sklearn.preprocessing import PolynomialFeatures를 통해 새로운 feature를 만들고 Linear Regression을 진행할 수 있다.
Learning Curves
모델 추정을 몇 차식으로 해야할까? 즉, 모델을 복잡도를 어떻게 결정할 수 있을까? (1차로 하면 underfitting이 발생할 수 있고, 차수를 너무 높이면 overfitting이 발생할 것이다.)
모델의 복잡도를 높이면 variance(민감도)는 높아지고, bias(잘못 추정)는 감소할 것이다.
Regularized Models
overfitting을 막기 위해서는 모델을 일반화시키는 것이 중요하다. 선형 회귀에서는 Ridge Regression, Lasso Regression, Elastic Net 이 세 가지 방법을 통해서 모델의 가중치를 제한할 수 있다.
학습 중에 coss function에 사용되어야만 한다. 아래는 Ridge Regression이다.

아래는 Lasso Regression이다. Lasso는 모델의 가중치를 정확히 0으로 만들어낼 수 있다는 특징이 있다. (여기서 모델의 가중치는 회귀계수라고 생각하면 될 것이다.)

파이썬에서는 from sklearn.linear_model import Ridge과 from sklearn.linear_model import Lasso를 사용한다.
Elastic Net은 Ridge와 Lasso의 사이라고 생각하면 된다. regularization term이 Ridge와 Lasso를 결합한 식으로 사용된다.
Early Stopping
validation error가 minimum에 도착했을 때, 학습을 종료하는 것이다. validation은 감소하고 중간에 다시 증가하는 경향이 있어, 다시 증가하기 이전에 학습을 종료하여 best model인 지점을 찾아내는 것이다.
overfitting을 방지하기 위해서는 Ridge/Lasso, Early Stopping, Dropout 방법이 있다.
Logistic Regression
몇 가지 회귀 함수는 분류 문제에 활용되기도 한다. 만약 추정 확률이 50% 이상이라면, 특정 범주에 속한다고 판단하여 분류에 사용한다.
로지스틱 함수는 시그모이드 함수를 사용한다. 시그모이드 함수는 값을 0에서 1 사이로 변경해준다.
로지스틱 함수의 cost function은 아래와 같고, log loss라고 부른다.

Softmax Regression
범주가 여러 개인 경우에 소프트맥스 함수를 사용한다. (softmax regression = multinomial logistic regression)
먼저 각 클래스에 속할 점수를 구하고, 각 범주에 속할 확률을 구한다. 그리고 분류할 값의 각 클래스에 대한 확률을 구하고 가장 높은 확률이 나온 클래스로 분류한다.
알맞은 클래스로 잘 분류되었는지 확인하기 위해서는 Cross entropy 개념을 사용한다.